基于数形结合思想的初中数学教学探究
2019-09-10陈垌满
陈垌满

【摘要】 丰富学生解题思路,提升学生解题能力,能够促进学生解题效率及整体成绩的提升。本文对数形结合思想进行了阐述,明确了数形结合思想常用的解题范围,并根据解题要点,给出具体的应用实例,为初中数学教育工作提供参考。
【关键词】 数形结合 初中数学 教学应用
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2019)02-102-02
前言
随着新课改的推进,初中阶段的数学教学对学生的解题技能提出了更多要求,培养学生数形结合思想能够有效提升解题效率,锻炼解体思维,促进学生学习成果及综合素质的共同提升。
一、数形结合的思想概述
数和形是数学研究中最为古老和基础的对象,在一定情况下,可以实现数与形之间的相互转化。常规的初中阶段数学研究被分为数、形两大部分进行独立研究,而数与形之间又存在必然的联系,将数与形进行结合研究,将其成为数形结合。数形结合的研究分为两种情形,一种是应用数字精准的属性阐述形的特征,另一种则是应用形的直观来阐述数字之间的关系,简单的讲二者关系理解为“以数述形”或是“以形表数”。
我国著名数学家华罗庚曾用一句话总结了数形结合理念关系,即“数形结合百般好,隔离分家万事休”由此可以看出应用数形结合有利于数学研究,而在研究中不能将数形单独区分进行研究。数形结合将精准的数字、抽象的数学语言与直观的几何图形、位置关系相结合,将复杂问题简单化、表象问题深入化、抽象问题具体化,从而简化学生解题路径,深化教师数学研究。
二、初中阶段数形结合的应用范围
数形结合的理念广泛应用于数学课堂教学工作中,数形结合的解题思路是数学教学中的主要工作之一,应用数形结合思路能够解决集合、函数、方程式、不等式、三角函數、数列、解析几何、立体几何、绝对值、分数应用等多种类型的题目。以函数、方程、不等式和三角函数为例,将数形结合应用于函数运算当中,借助图像来表现函数的性质,将函数图像的几何特征与数量特征充分结合利用;在解答方程式与不等式的过程中,可以将方程问题看作是两个函数图像的交集,将不等式的计算应用数形结合从题目条件即结论着手,联系相关函数,重点突出几何意义,应用图像寻找不等式的求解思路;数形结合思想是三角函数问题处理最重要、有效的解答办法,在解答三角函数问题时,数形结合应用在单调区间、函数值大小问题的解答,借助单位圆或三角函数的图像进行处理。
三、数形结合在初中教学中的具体应用
(一)数形结合思想的应用要点
1.数形结合是在解答数学问题中常用的解题思想,结合数形结合思想的解答过程们能够使抽象的问题更加直观、具体,使学生对于问题的理解更加直观、深入,从而把握该问题的本质及出题人的考察用意;应用数形结合方法,促进解题效率及质量的提升,学生对数学学习的热情也会在某种程度上得到提升。
2.数形结合,是根据数与形的联系,通过数形的相互转化以解决部分较为复杂的数学问题,要实现数形集合,会应用到以下几个知识点:1.实数在数轴上的点坐标关系;2.函数与图像的关系;3.曲线与方程的关系;4.几何与几何参数的关系等。
3.从历年的中考、高考试题来看,应用数形结合思维,能够解决大部分考试中的难题难点,促进学生解题能力和成绩的提升。
4.应用数形结合的思想能够直观的发现解体的突破口,将复杂的问题简单化,减少解题步骤和计算过程,从而降低疏漏发生的机率,提升解题效率,在考试中又更多的时间对必拿分的题目进行反复检测,促进分数整体提升。
(二)初中数学阶段数形结合思想应用的距离说明
数形结合的应用广泛,本文以图形证明问题、函数问题及不等式问题为例,距离说明数形结合在初中阶段数学教学工作中的应用。
1.图形证明问题
初中阶段的数学教学中,图形证明题是重点也是难点,例如要证明两个三角形全等,常规的解决方法是画辅助线,将辅助线作为解答的突破口,但在解答过程中,部分学生因为抽象思维、几何思维较为薄弱,不会应用辅助线或辅助线不准确,此类问题就难以解答,在考试中是丢分项。面对此问题教师可以引入数形结合思想,以图形教育为基础,引导学生思维发散,通过引导学生逐渐在脑中形成“烙印”,逐渐对该类题型形成思维定式,意识到辅助线在问题解答中的意义。在此情况下,学生遇到该类型问题时,第一反应就是应用辅助线,并根据题型积累,快速敲定辅助线的位置。
例1:应用图形的几何意义证明完全平方公式
证明:将边长为a的正方形增加边长b,形成两个正方形与矩形,具体如图1所示。
∵此图形的面积可以表示为(a+b)2或a2+2ab+b2
∴(a+b)2=a2+2ab+b2
根据此因果关系可以炎症两数之和的完全平方公式。
类比解决:
在课堂上教师可以引导学生类比此方法,应用图形几何意义证明平方差公式,要求以图形表示并明确推理过程。
提问:如何应用图形几何意义证明:13+23=32?
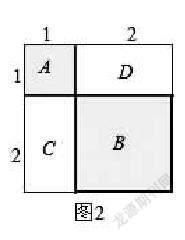
如图2所示,一个A的面积以1×1×1=13表示
B的面积是正方形以2×2表示,而CD可以组成一个正方形面积以2×2表示,因此BCD三个区域的面积总和可以看作是2个边长为2的正方形,表示为2×2×2=23,而图2整个面积总和可以看作是一个边长为1+2的正方形,则面积表示为3×3=32.由此可以得出结论13+23=32.
以此类推,学生继续探究 13+23+33=?,13+23+33+…+n3=?
2.一次函数及二次函数的解答
初中阶段学习的函数主要为一次函数及二次函数,二者具体的函数表达式为:y=kx+b以及y=ax2+bx+c,进一步又会细分为一元函数、二元函数等。从二者的表达式来看,学生难以理解函数的性质,即单调性与对称性,这就导致学生难以理解和解答问题。
结合数形结合的函数解答,教师应用函数中几个代表性的做好,以图形的形式将抽象的函数性质表达。在课堂教学中向学生介绍一次函数是存在于坐标系一三象限或二四象限的直线,学生就会了解一次函数是单调函数且随着数值的变化直线递增或递减,且横向、纵向具有不对称性。二次函数从图像可以看出在部分区间有单调性,且并非直线递增、递减,并沿y轴对称。
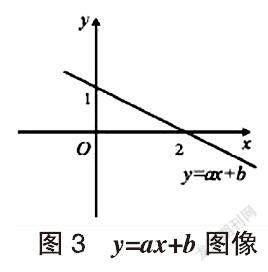
例2:一次函数y=ax+b的图像如图3所示,求一元一次方程ax+b=0的解。
該题目考察一次函数与一元一次方程的联系。一元一次方程的解即x值,是当一次函数y=0时,x的数值,或是求一次函数图像与x轴交点横坐标的值。由图像可以看出一元一次方程的解x=2.
3.解答不等式
在解答不等式时,要充分利用数轴,在解答不等式是时,数值会对应多个区间,而应用数轴即可将数字在数轴上具象化,进而分析数轴上的重合点,即可求解该不等式未知数的求解范围。
例3:教师可以在不等式教学时,利用例2进行引申,促进知识的迁移与思维变通,教师启发学生如果ax+b>0,那么需要截取函数直线在X轴以上的部分,以x=2为临界点,那么该不等式的解集就是x<2,同理ax+b<0的解集是x>2.
总结
综上,数形结合的思想对初中阶段学生的数学学习直观重要,教师要优化教学理念,将数形结合思想广泛应用于数学教学中,在本文实例的基础上学以致用,优化创新,丰富学生解题技能,促进学解题效率及解题能力的提升。最为重要的是将数形结合的思想深入人心,使之根深蒂固,保障学生在任何学龄段、任何层次都能对此思维灵活应用。
[ 参 考 文 献 ]
[1]杨娥.基于数形结合思想的初中数学教学实践研究[J].新课程(中),2017(4):42-42.
[2]朱国暹.数形结合思想在初中数学教学中的应用[J].林区教学,
