根据微积分理论来认识康托集合论的错误

四川省攀枝花市老年科学技术工作者协会 张喜安

康托集合论的基本观点是：一个无穷集合可以和它的一个真子集一一对应，部分可以和全体相等。这个观点正是康托集合论的一个定理，现在我们称这个定理为康托集合论的基本定理，为了论述得方便，我们把这个定理及其证明引述如下：

康托集合论的基本定理 令a，b为实数，并且a＜b，则[a，b]的基数等于[0，1]的基数。

证明：令y=f(x)=a+(b-a)x，显然y=f(x)为[0，1]→[a，b]的双射函数，这就证明了[a，b]的基数等于[0，1]的基数。

这个定理表明一个无穷集合可以和它的一个真子集一一对应，部分可以和全体相等。例如，由于存在函数y=2x为[0，1]→[0，2]的双射函数，所以[0，1]和[0，2]为一一对应的关系，这时无穷集合[0，2]和它的真子集[0，1]一一对应，部分[0，1]和全体[0，2]相等。

为了证明康托集合论是错误的，我们将以具体的例子来证明康托集合论的基本定理的证明不能成立。

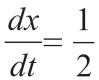
再有，在[0，1]在x轴上，[0，2]在y轴上，在y=2x的时候，[0，1]和[0，2]是一一对应的关系，这时，我们还要注意到，在y=x的条件下，[0，1]和[0，2]却是非一一对应的关系。这时我们要问，[0，1]和[0，2]是一一对应的关系，还是非一一对应的关系？这表明，康托的两个集合间一一对应的定义是不能判断两个实数点的集合是不是一一对应的关系。同时我们还要注意到，康托集合论的两个集合间一一对应的定义是一个全称量词命题，如果这个命题是正确的，它就不可能存在相反的命题，但是在y=x的条件下，[0，1]和[0，2]就是非一一对应的关系，这就是一个相反的命题，这个事实说明，康托集合论的两个集合间一一对应的定义是错误的。这个定义是康托集合论的基础，它是错误的，说明康托集合论也就是错误的。

根据以上的分析，我们可以得出结论，康托集合论的基本定理的证明不能成立，因此康托集合论是错误的理论。