数学教学：浅谈排列组合中的“球入盒”问题

江苏省昆山中学 蔡丽菊

在高中数学中有《排列组合》这一章，对学生逻辑推理能力、分类讨论以及建构模型的能力都有极高的要求，包括现在的数学竞赛中都涉及排列组合问题。其中，“小球与盒子”的模型问题一直是一个热门话题。由于球与盒子都有着“相同”与“不同”的分类，并且具有知识上的综合性、解题技巧上的灵活性以及思维方式上的抽象性，使同学对此类问题感到很是困惑，感觉千变万化，无从下手。下面我就对此模型问题的解法及运用作一个总结和分析，望同学有所感悟。

类型一：不同小球入不同盒子的模型

1.球少盒多型

例1：若将4个不同的小球，放入5个不同的盒子里，有几种不同的放法？

变式1： 若将4个不同的小球，放入5个不同的盒子里，每盒至多放一个，有几种不同的放法？

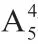
变式2：若将5个不同的小球，放入5个不同的盒子里，每盒至少放一个，有几种不同的放法？

注：此类问题一般用排列组合思想，利用分步计数原理

2.球多盒少且每盒至少放一球型

例2：若将5个不同的小球，放入4个不同的盒子里，每盒至少放一个，有几种不同的放法？

变式：若将5个不同的小球放入4个不同的盒子里，恰有1个空盒，有几种不同的放法？

注：此题型应该先分组，后排列。

类型二：相同小球放入不同盒子的模型

例3：若将10个相同的小球，放入3个不同的盒子里，每个盒子不空，有多少种不同的放法？

变式1： 若将10个相同的小球放入3个不同的盒子里，允许盒子空，有多少种不同的放法？

变式2：若将10个相同的小球装入3个编号分别为1，2，3的盒子，要求盒子里球的个数不小于盒子的编号数，这样的装法总数是多少？

解：此题分两步，先将编号为1，2，3的3个盒子分别放入0，1，2个球，再把剩下的7个球分成3组，即在这7个球中间的6个空档中放入两个相同隔板,自然分成3组，代表放入三个不同盒子中。即3个盒子此时小球肯定不小于编号数了。故有 种放法。

应用3（名额分配问题）：将10个三好生分配给3个班级。

（1）每班至少一个,则共有多少种分配方法？

（2）任意分配共有多少种分配方法？

（3）若班级为一、二、三班,三好生人数不少于班级数,则共有多少种分配方法？

解：由于10个三好生是相同的,那么就等价于10个相同的小球放入3个不同盒子。

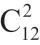
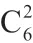
注：如果是处理“相同元素不同组”模型时,我们都可以用“隔板法”；如果每组元素数为至少一个时,可用插“隔板”；如果出现每组元素数为0个时用排“隔板”。

【归纳小结】其实小球入盒是排列组合中非常典型的问题，还有像方程解的问题和名额分配等问题，虽然形式多变，但实际与小球入盒问题是等价的。小球入盒可以分为4类：不同的小球放入相同的盒子里；不同的小球放入不同的盒子里；相同的小球放入相同的盒子中；相同的小球放入不同的盒子里。解决小球入盒问题最高效、最准确的方法是“先分组，后分配”,解答相同小球入不同盒子问题的最有效、最简易的方法是隔板法。虽然看起来很复杂，其实只有搞清楚类型，注意小球和盒子的“同”与“不同”，对号入座，再次结合两个计数原理，我相信对同学提高此类问题的解题能力一定是有所帮助的。