炸药撞击刚性靶板的试验和数值模拟

2019-08-13贾宪振王永顺刘瑞鹏

兵器装备工程学报 2019年7期

贾宪振,王永顺,刘瑞鹏

(西安近代化学研究所，西安 710065)

炸药的撞击安全性是实际当中十分关心的问题，目前国内外已经开展了广泛的研究[1-4]，研究者大多采用炸药被动撞击的方式。然而对于炸药服役期间的一些工况，如弹体高速侵彻目标靶板、弹体入水和弹体跌落撞地等，炸药均为主动撞击，所以有必要研究炸药在主动撞击条件下的响应特性，以指导炸药配方和装药设计[5]。因此，开展了药柱以一定速度撞击刚性靶板的研究，分析了药柱撞击刚性靶板的大变形和破碎等动态响应规律，重点研究了药柱撞击靶板过程中的点火机制。

药柱撞击刚性靶板的过程属于非线性的瞬态问题，理论分析较为复杂。同时，由于炸药撞击试验潜在的爆炸破坏性，导致试验能够获取的数据十分有限，而采用数值模拟方法可以展示更多的炸药撞击过程的细节，从而揭示药柱撞击过程中的响应规律和点火机制。

1 药柱撞击刚性靶板试验

图1为炸药撞击刚性靶板试验系统的示意图，该系统主要由发射装置、测速装置、回收装置、高速摄影和钢质靶板等几部分构成。其中，发射装置为30 mm口径的火炮，发射时药柱嵌套在专用弹托上，弹托的作用有两个：一是防止药柱与火炮中的高温高压气体直接接触而提前点火；二是保持药柱飞行的气动稳定性。药柱和弹托在药柱撞靶前会自动分离，从而不会影响药柱的撞靶过程。测速装置由电子测时仪和网靶组成，用来测试试样的飞行速度，高速摄影用来拍摄炸药的撞击及点火情况，钢质靶板固定于地面上，其强度足够大，以保证在炸药撞击过程中靶板不发生塑性变形。

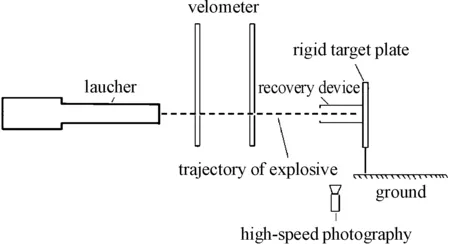
图1 炸药撞击刚性靶板试验系统示意图

试验药柱由PBX-3炸药和壳体两部分组成，壳体为圆筒状，壁厚为1 mm，材质为聚四氟乙烯(PTFE)，底部厚度为1 mm。样品采用直接浇注法注入壳体内，药柱尺寸为Ф18×23 mm，试验样品如图2所示。

图2 试验药柱样品实物图

对PBX-3炸药进行了不同速度下的撞击试验，试验结果如表1所示。根据表1，PBX-3炸药在撞击刚性靶板时的临界点火速度在431～434 m/s之间。

表1 PBX-3炸药撞击刚性靶板试验结果

图3给出了撞击速度分别为434 m/s和446 m/s时的点火反应照片。当撞击速度为434 m/s时，药柱虽然发生了点火，但是只有少部分药柱发生了燃烧，产生图3(a)中的火光后便逐渐熄灭。而当撞击速度为446 m/s时，药柱点火后迅速反应，火光覆盖整个靶板，并持续较长时间，说明药柱基本全部参与反应。

图3 两种撞击速度下药柱的反应情况对比

2 数值模拟

2.1 问题分析

假设炸药试样呈细长圆柱形，并以一定速度V轴向正撞击刚性靶板，药柱的密度为ρ0，声速为c0，如果V足够小，那么撞击之后药柱内部产生弹性应力波，其幅值σ为[6]

σ=ρ0c0V

(1)

如果撞击速度足够高，产生的应力幅值就会超过炸药材料的屈服应力Y，在临界状态产生的应力幅值对应于屈服应力水平的撞击速度，即屈服速度VY，其计算公式为

(2)

材料声速可以根据材料的弹性模量E和密度ρ0得到：

(3)

根据式(2)、式(3)得到：

(4)

根据文献[7],药柱的弹性模量在10 GPa左右，屈服应力一般在50 MPa以内，密度在(1 500～2 000)kg/m3，因此根据式(4)估算，药柱的屈服速度在10 m/s左右。而根据撞击试验，能够导致炸药点火的撞击速度都在102 m/s量级上，该速度已经远远大于炸药的屈服速度。因此，炸药在102 m/s量级的速度下撞击刚性靶板，必然发生大变形和破碎。

2.2 计算方法

对于材料大变形和破碎过程的数值模拟，采用拉格朗日共节点方法容易导致局部网格大变形甚至畸变，造成计算困难[8]。该方法示意图如图4，图4中共有4个单元，共计9个节点，其中节点2、4、6、8被两个单元所共用，而节点5被4个单元所共用。

图4 拉格朗日共节点法示意图

在处理大变形问题时，为避免网格变形过大导致计算出错，拉格朗日共节点法通常采用侵蚀算法，即设置一个网格侵蚀的阈值，当达到该阈值时，网格自动删除，从而保证计算能够进行下去。但是，直接删除网格会带来计算的“失真”，不仅使整个物理过程发生改变，同时造成无法计算大变形部位的应力状态和温度变化，从而丢失实际当中关心的重要信息。

针对上述问题，本文采用“节点约束-失效法”计算药柱的大变形和破碎过程，同时结合热力耦合算法计算药柱在撞击过程中的温度变化。“节点约束-失效法”在建模时不再采用共节点法，图5给出了“节点约束-失效法”示意图，同样以4个单元为例进行说明。4个单元共计16个节点，这些节点在建模时是相互独立的，同时将位置重合的节点定义节点组，如图5中共计定义了5个节点组(每个虚框内即为1个节点组)，其中节点组1、2、4、5都包含两个节点，而节点组3则包含4个节点。处于同一节点组的节点在初始时约束在一起，具有相同的位移、速度等力学参量，随着变形的增大，当塑性应变大于一定的阈值时，处于同一节点组的节点约束便失效，这些节点不再被约束在一起，从而可以模拟大变形过程中的裂纹、破碎、飞散等现象。

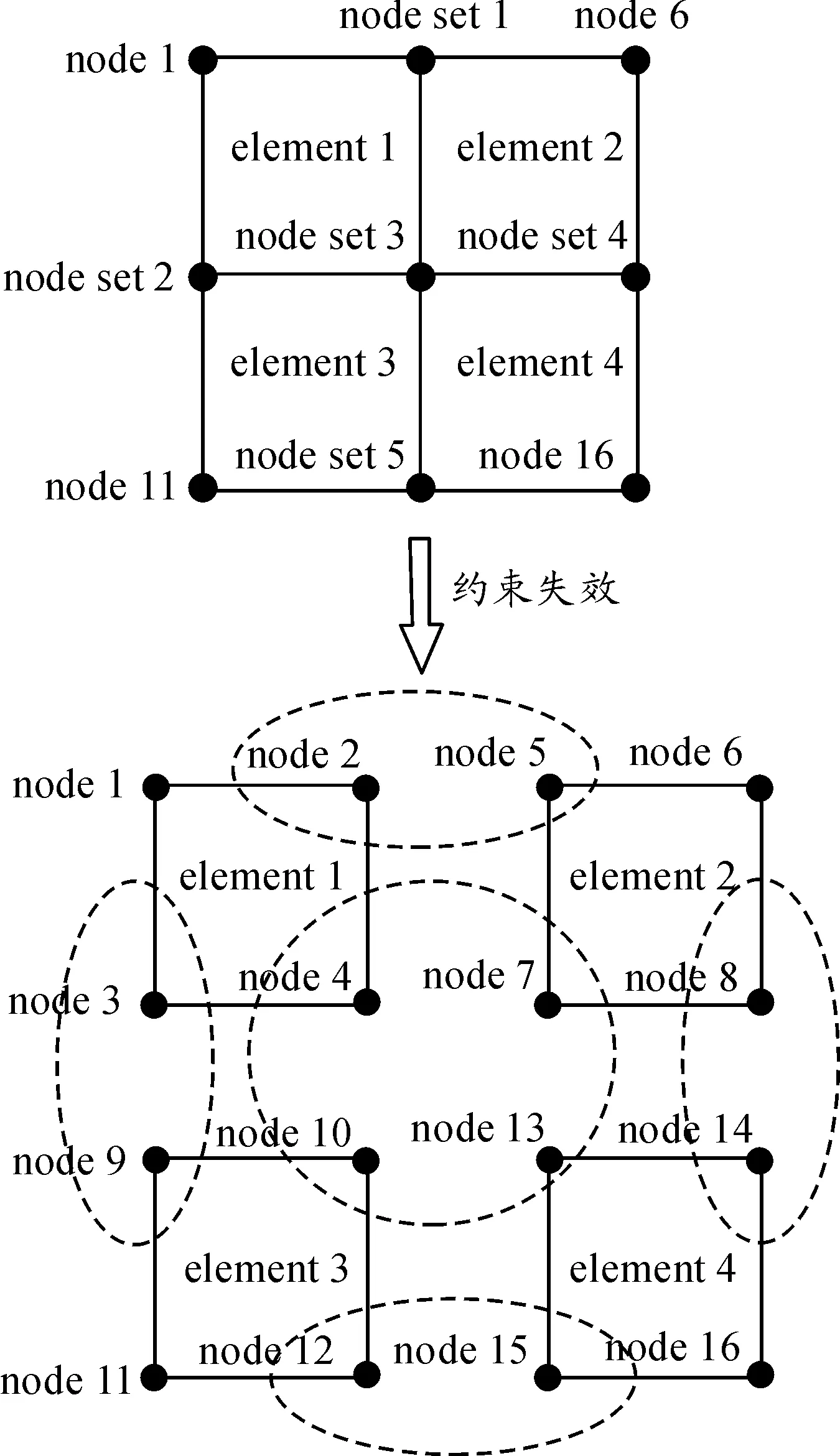
图5 节点约束-失效法示意图

图6为基于“节点约束-失效法”建立的药柱撞击钢板的仿真模型，模型包括药柱、PTFE壳体和钢板3部分。数值模拟前期，对不同的炸药网格尺寸进行了试算，结果表明：当网格尺寸为0.45 mm时，计算结果趋于稳定，此时进一步细化网格对计算结果的影响已经很小，但是却会使计算量大幅增加，由此确定仿真模型中药柱的网格尺寸为0.45 mm。

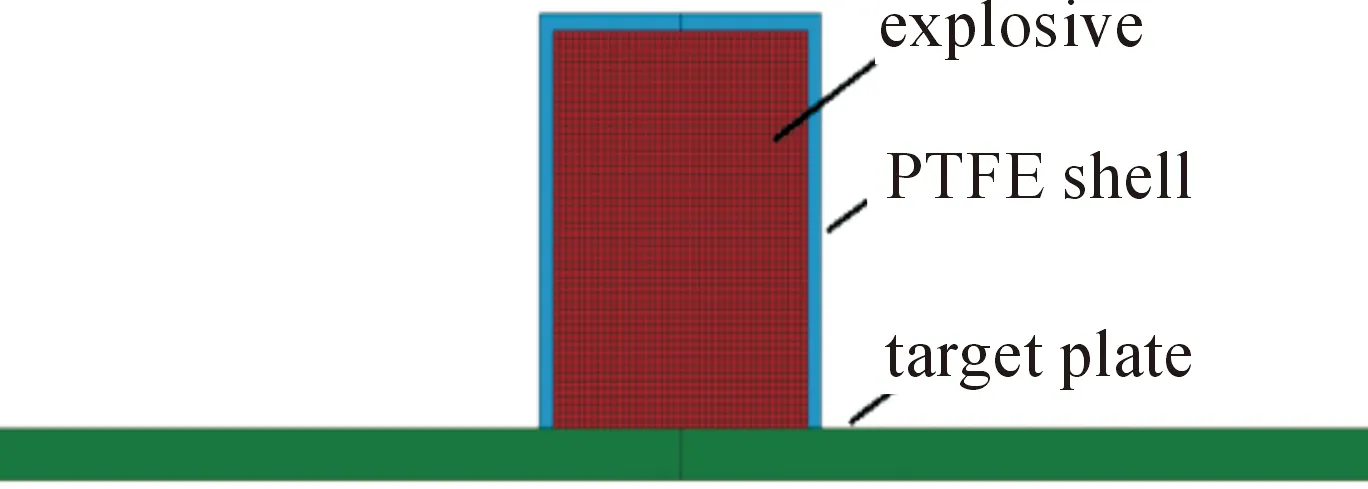
图6 药柱撞击刚性靶板仿真模型

2.3 材料模型

炸药力学模型采用热弹塑性材料模型，其本构关系为[9-10]

(5)

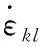
(6)

式(6)中，E是弹性模量，ν是泊松比。

通过下式判断材料是否发生塑性变形：

(7)

式(7)中，sij为应力偏量，σy(T)为屈服应力，计算公式为

(8)

σ0(T)为初始屈服应力，Ep为塑性硬化模量，σ0(T)和Ep均为温度的函数。

当材料处于塑性状态时，应力偏量计算公式如下：

(9)

式(9)中，fs为缩减系数，其计算公式为

(10)

(11)

炸药的热学模型采用各向同性热传导模型：

(12)

式(12)中，cv为材料比定容热容，λ为热导率，Qs为材料内部的热源，其计算公式为

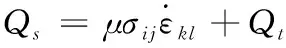
(13)

式(13)中，μ为功转热比率，Qt为炸药热分解放热量。

炸药化学反应模型采用Arrhenius方程，由于炸药点火时的反应度很小，所以可以忽略炸药从自热到点火过程中炸药反应物浓度的变化，根据下式求出化学反应放热量Qt：

(14)

式(14)中，Q为炸药的反应热，A为指前因子，Ea为活化能，R为普适气体常数。

由实验测得了PBX-3炸药的材料参数值，如表2所示。

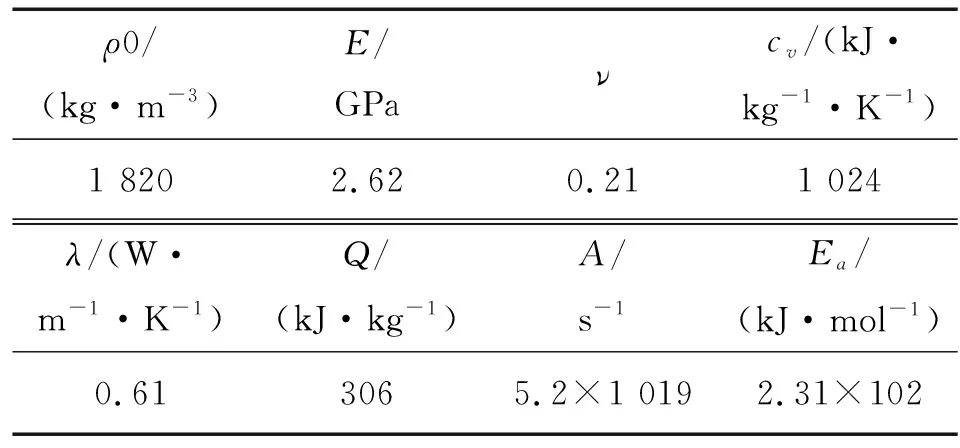
表2 PBX-3炸药的材料参数值

2.4 计算结果与讨论

首先分析药柱在撞击速度较低未发生点火时的变形和破碎情况。图7给出了撞击速度为405 m/s时的药柱演化过程，此时药柱没有点火。为了检验计算精度，采用ANSYS AUTODYN程序的欧拉算法进行了计算，用来与“节点约束-失效法”的计算结果进行对比，图7同时给出了Euler算法的计算结果。可以看出：两种算法计算得到的药柱变形过程基本一致。在撞击过程中，药柱撞击面的形状是内凹的，药柱高度逐渐减小，药柱被迅速压扁，并且沿着撞击面向四周飞散。当撞击产生的应力波尚未到达药柱尾端时，药柱尾端呈平面状，而当应力波达到药柱尾端之后，药柱尾端呈鼓包状。两种算法的结果差异主要体现在撞击后期，即在40μs 以后，“节点约束-失效法”已经计算出了药柱中出现的裂纹和破碎现象，药柱的破碎分布在药柱与靶板的撞击面上，其计算结果与理论分析更符合，而欧拉算法则无法计算出裂纹和破碎等现象。总的来说，“节点约束-失效法”的计算更好地反映了药柱在撞击过程中的破碎现象。

进一步增加撞击速度进行数值模拟，结果发现当撞击速度为430 m/s时药柱发生了点火，进一步增加撞击速度，药柱的点火时间提前。图8给出了不同撞击速度下药柱发生点火时温度云图，并对温度最高处进行了局部放大，图8中给出了药柱温度最高处的位置，也就是点火位置。可以看出，药柱点火的位置位于撞击面上，略靠近药柱径向边缘，由于这一位置处的炸药同时受到撞击压缩作用和摩擦作用，所以升温速度较快，最先发生点火。

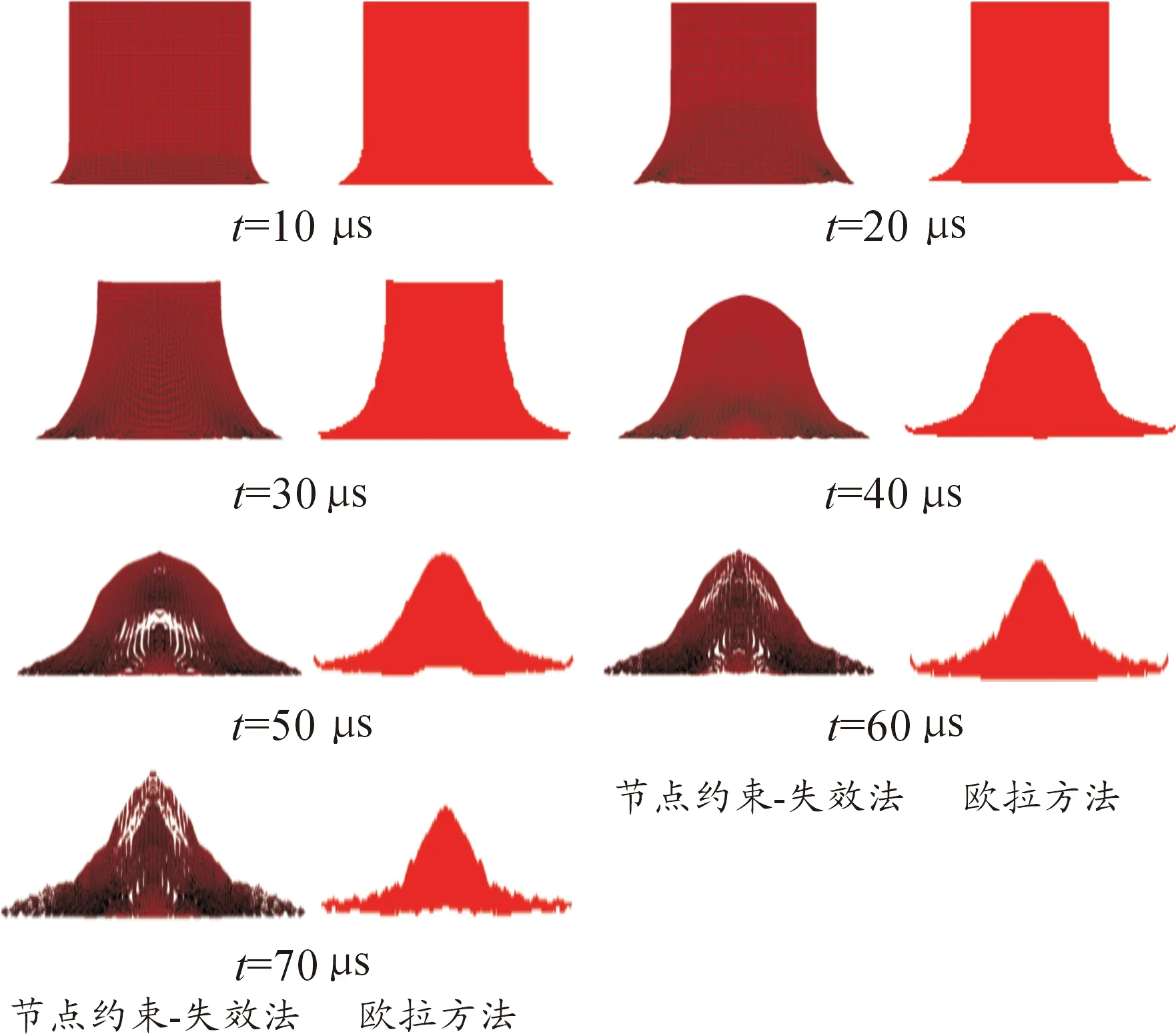
图7 不同算法下炸药形态的演化过程

图8 不同撞击速度下药柱点火时的温度云图

图9给出了不同撞击速度下药柱最高温度点的温度曲线。根据图9，在撞击开始阶段，温度均是在短时间内迅速上升，这是由于该阶段内药柱撞击刚性靶板产生塑性应力波，塑性应力波导致药柱产生塑性大变形，药柱的动能通过塑性功转热的过程转化为炸药的内能，使炸药温度迅速上升，随着撞击速度的增大，塑性应力波的幅值也增大，药柱的塑性变形和塑性功转热也逐渐加剧，所以药柱最高温度点的温度曲线随着撞击速度的增大而逐渐升高。

对比图9中的3条曲线，可知当撞击速度为380 m/s时，药柱的温度到达一定值后逐渐趋于稳定，说明炸药没有点火。当撞击速度为405 m/s时，药柱的温度也达到一定值后便不再上升，并且该温度值比撞击速度为380 m/s时的高一些。

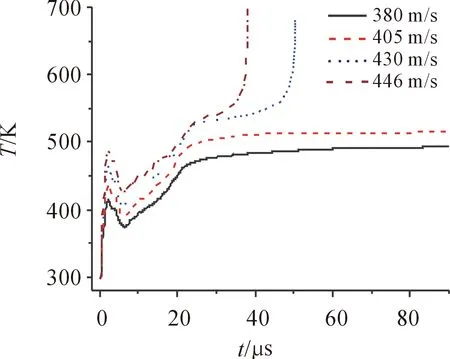
图9 不同撞击速度下炸药温度最高点的温度曲线

当撞击速度为430 m/s时，药柱的温度升高到一定温度后出现拐点，然后呈突跃式上升，达到650 K以上，说明此时药柱已经发生了自加速反应，即发生了点火。当撞击速度为446 m/s时，药柱的温度升高更为迅速，温度曲线发生突跃式上升的时间提前。

根据计算结果，随着撞击速度的增大，药柱的最高温度逐渐升高，当撞击速度达到临界速度时，药柱开始出现自加速反应而点火。结合图7和图8可知：对于PBX-3炸药，其临界撞击速度约为430 m/s，与试验结果基本一致。当药柱以临界速度撞击靶板时，药柱发生点火的时间发生在药柱破碎以后，而且点火位置就位于破碎区，各炸药碎块之间已经存在一定的距离，导致点火之后不易迅速传播，从而造成只有少量炸药反应。而当炸药的撞击速度明显高于临界速度时，药柱在发生点火时尚未完全破碎，从而就既有可能导致使全部药柱发生反应。