可旋转多向组合机构的运动学仿真及力学分析

2019-08-13俞海涛赵术杰

兵器装备工程学报 2019年7期

俞海涛，邵飞，徐倩，赵术杰

(陆军工程大学野战工程学院，南京 210007)

总体结构型式是设备实现其性能指标的基础，很大程度上决定了设备综合性能的高低，但现有设备所采用的架设方式与架设装置难以满足新功能的要求[1-2]。在目前的机械设备中，旋转机构是应用最为广泛的机构之一，简单的轴系机构已不能满足复杂的功能要求。复杂的旋转架设机构如果通过传统的设计方法，即先通过样机反复试验并改进的方式即会消耗掉大量时间，也会使经费大大增加。因此，在制备样机之前，运用仿真技术提前改进设计缺陷既可以缩短设计周期，也可以减少经费的使用[3-5]。本研究将进行可旋转多向组合机构的运动学仿真，根据初步设计的机构构件，在Solidworks中进行可旋转多向组合机构实体模型建立，利用Solidworks motion插件进行运动仿真。仿真主要为分析不同架设时间下的车辙不同速度和角速度的影响。根据在运动分析的结果，再对旋转接头和旋转连接块的力学分析。

1 旋转机构

机构如图1所示。桥跨连接机构分为纵向连接和横向连接两部分。体系转换机构的方式采用顶升—旋转—下落固定的方式，由一套可旋转架设机构完成此功能。旋转组合机构主要用于对桥跨模块在车轴线与垂直车轴线之间进行转换，主要由可旋转立柱、升降油缸、旋转机构等组成。图1为旋转组合机构示意图，图2为旋转机构示意图，由集成面板、旋转油缸、滑动导槽、联板、作业臂、油缸支撑板等组成。

图1 旋转组合机构示意图

2 运动学模型建立

在运动仿真中，Adams能够实现多刚体系统的运动学和动力学仿真，如今Solidworks已经将其整合至Solidworks motion插件中[6]，因此，可以在Solidworks中实现旋转架设机构的运动学仿真。

2.1 几何建模

由于桥跨结构和架设装置是左右对称的，为减少建模和计算量，建立二分之一模型。模型只模拟旋转变换阶段的架设过程，不需要顶升油缸的作用，因此模型舍去顶升油缸。模型主要由12种构件组成，构件总数为39件，模型如图3所示。

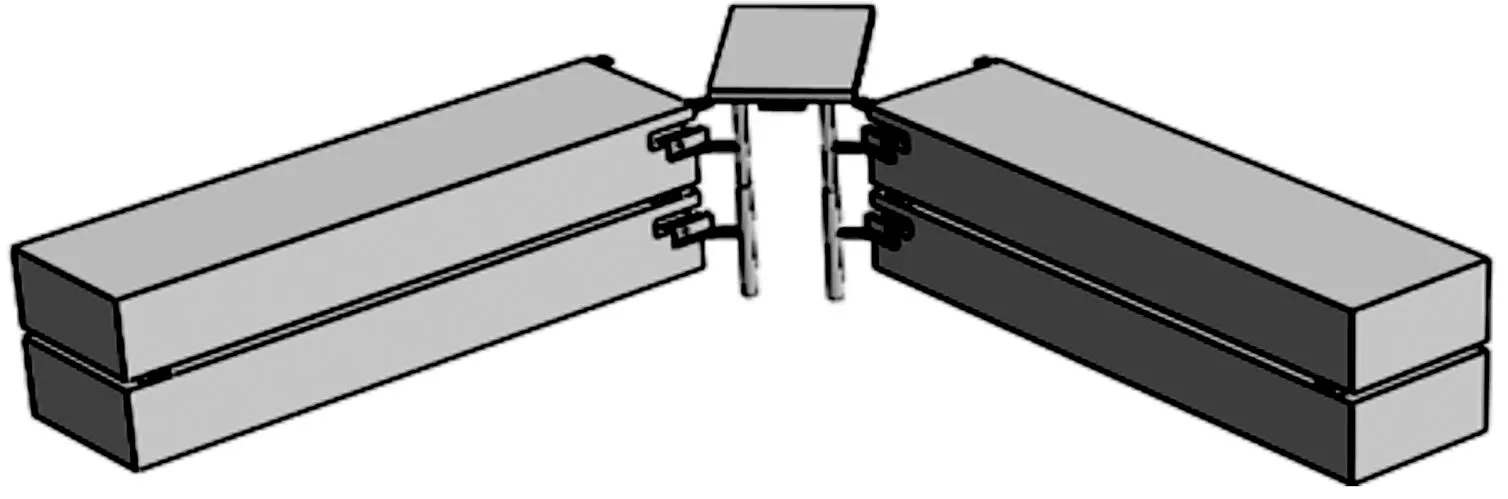
图3 运动仿真模型

2.2 创建约束

在运动仿真中，构件与构件之间的约束会影响到最终的运行轨迹[7-8]。为了简便旋转变换阶段的分析，将在此阶段中与集成面板不发生相对位移的构件都设置为固定，其中包括旋转立柱、旋转接头和滑动导槽3种共计5个构件。桥跨与车辙旋转连接块、顶紧块和多功能承压板通过3个维度的位置限制，实际已经是一个整体。旋转立柱与车辙的旋转连接块连接，旋转接头与旋转连接块的配合方式为同轴心配合。联板与车辙多功能承压板采用铰链配合，这种配合方式可以不建立两个零件之间的连接轴就能实现两种零件的运动仿真。滑动块通过配合只能沿着限位板的滑槽运动。滑动块与旋转油缸和作业臂的位置是固定的。

2.3 仿真分析

在运动仿真中，主要是对第二过程旋转变化的仿真模拟。旋转变换的操作过程是在顶升连接的基础上，旋转油缸开始缩短。此时，作业臂顺着滑动导槽带动联板运动，联板又带动车辙旋转。在整个旋转变换的过程中，旋转立柱式固定的，车辙是以旋转立柱的阳接头为轴心旋转的。当车辙旋转90 s时，顶升油缸停止运动。至此，旋转变换过程完成。

3 运动仿真计算与分析

在模拟中采用等速和距离两种方式进行模型的驱动，整个模型的单位系统选择为MMGS(mm、g、s)[9-10]。马达的运动类型选择线段的形式。首先设置位移曲线，选择CUBIC(default)的曲线形式。位移的大小设置为138 mm，以10 s为运动时间。计算出速度和加速度曲线，以桥跨远离旋转机构的表面为载体，提取其在运动过程中的角速度和速度等曲线。10 s完成旋转时车辙的最大速度与加速度历程如图4所示。

车辙表面的法向加速度很小，所以图4选取切向加速度代替加速度。从图4可以得出，当车辙刚开始旋转时，速度和角速度都不大，但是切向加速度和角加速度都较大，然后慢慢减小。当速度和角速度达到最大时，切向加速度和角加速度都为零。之后切向加速度和角加速度小于零，速度和角速度都开始减小。当10 s时，速度和角速度都为零；在速度与角速度最大的一刻，加速度与角加速度为0相反；在加速度与角加速度最大一刻，速度与角速度为0。

在整个运动过程中，能量输出是由马达完成。马达力-时间关系图和马达的能量输出功率-时间曲线如图5所示。

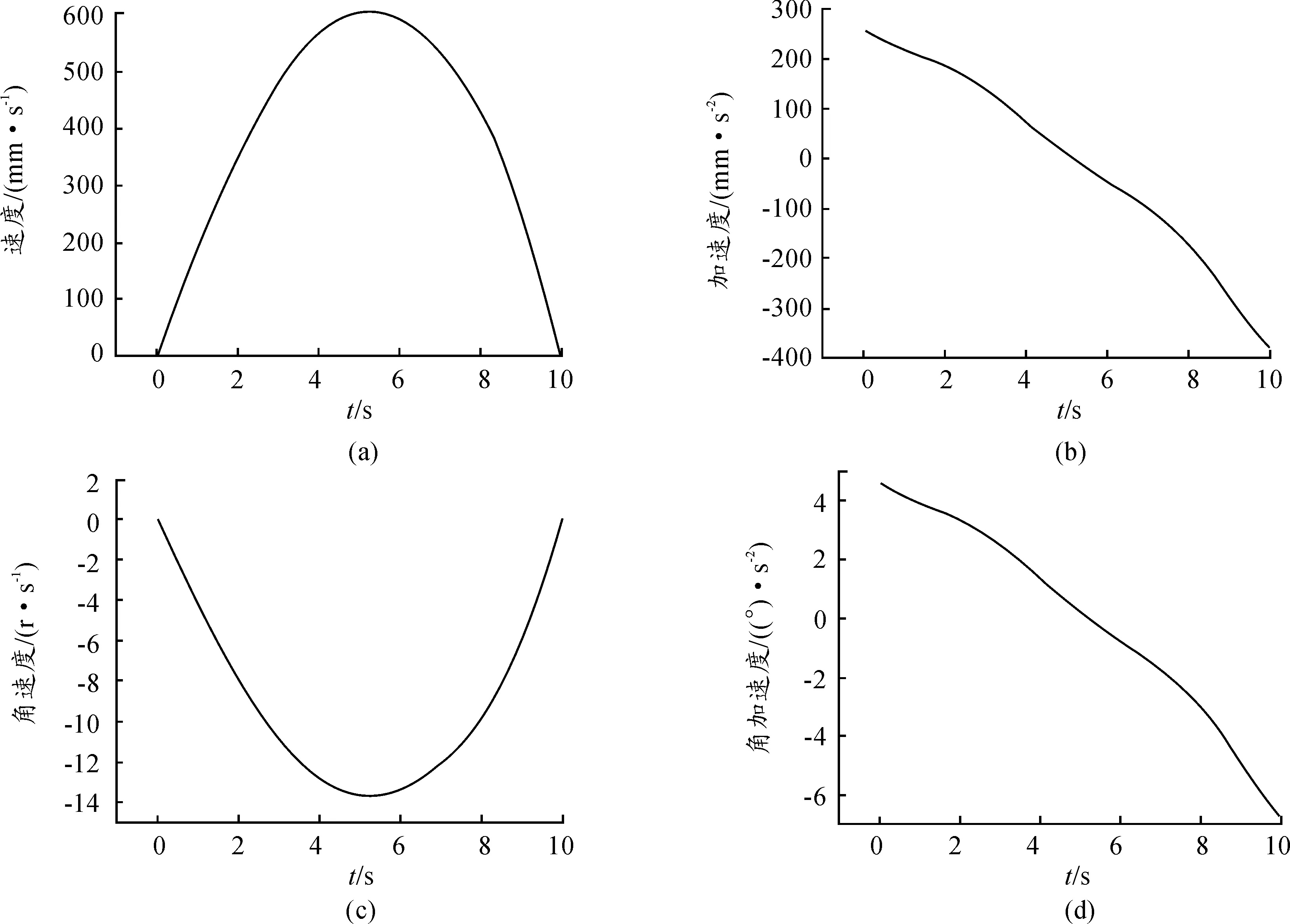
图4 10 s完成旋转时车辙的最大速度与加速度

图5 马达力及功率-时间曲线

从运动仿真结果表明可旋转多向组合接头机架设机构可满足门桥结构要求，但10 s的架设时间是比较短的，下面模拟15 s、20 s、25 s、30 s旋转架设时间，其速度-时间曲线如图6，马达力-时间曲线如图7，马达输出功率-时间曲线如图8。

为了方便查看各种数据，表1中列举了不同旋转架设时间下，最大与最小速度、马达力和马达输出功率。以及将对比数据归一化，分析各仿真计算结果随旋转时间变化趋势，如图9所示。

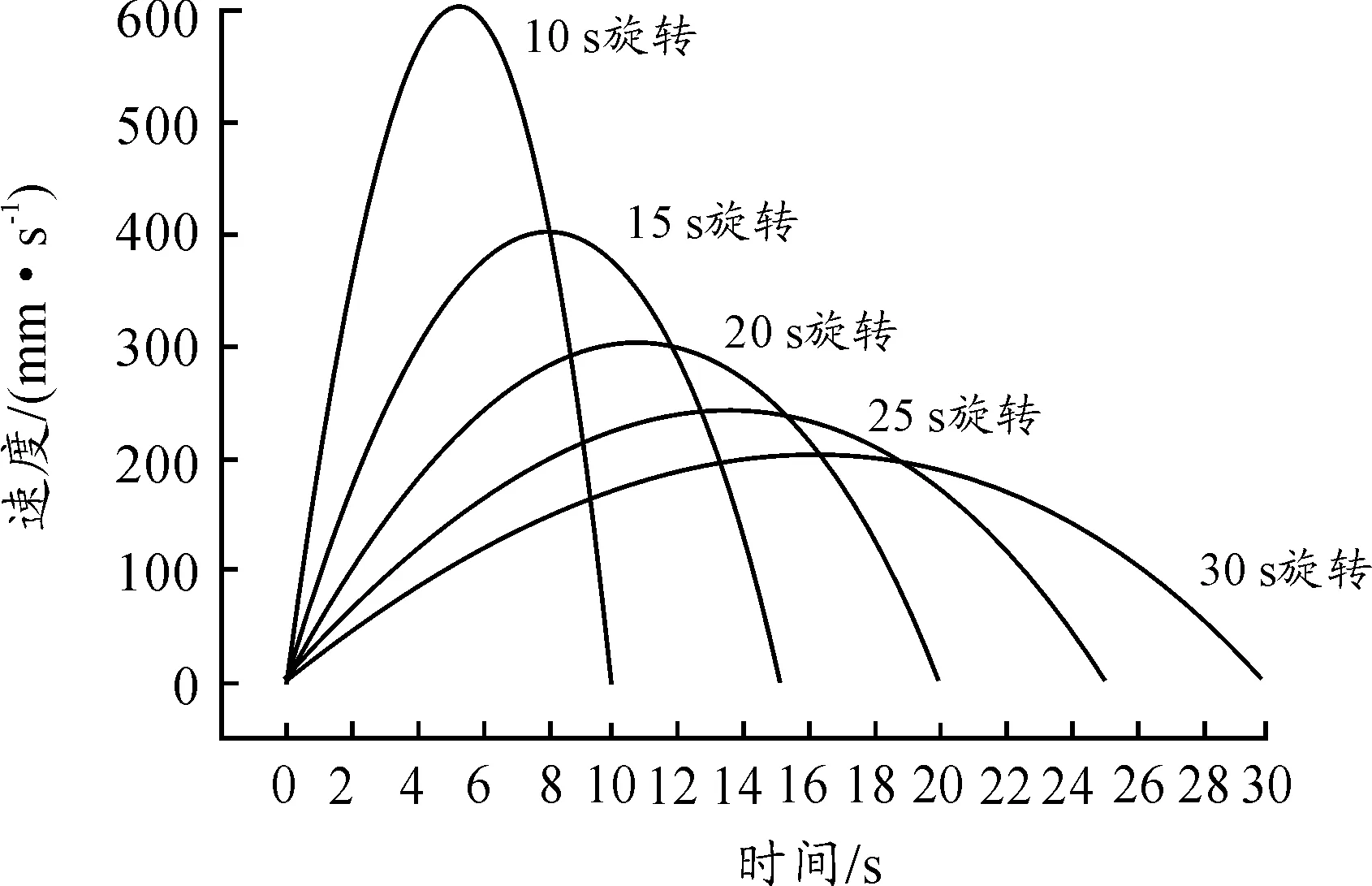
图6 多种旋转时间下的速度-时间曲线

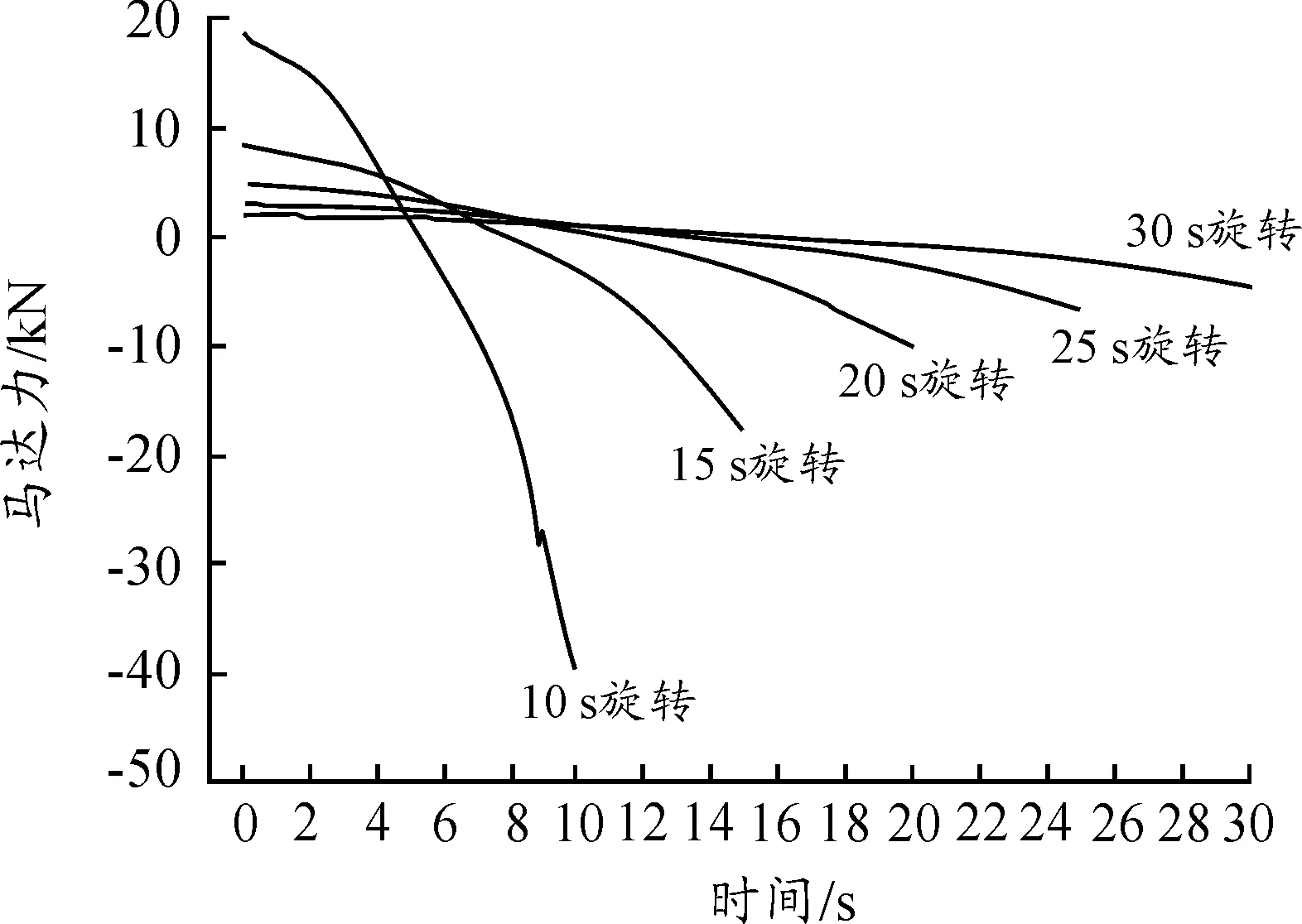
图7 多种旋转时间下的马达力-时间曲线

图8 多种旋转时间下的马达输出功率-时间曲线

旋转时间/s最大速度/(mm·s-1)最大马达力/N最小马达力/N最大功率/W1060418 776-39 852210232154038 379-18 10164-74203014 739-10 18126-31252323 039-6 51613-16302012 113-4 5258-9

图9 不同旋转时间下仿真计算曲线

从图9可以看出，随着架设时间的增加，车辙的马达力与马达输出功率的峰值都迅速减小，且减小的程度呈指数形式；而最大速度呈接近线性的程度下降。说明当架设时间有较小的减小时，对油缸的要求会有较大的提高；相反，当架设时间有较小的增加时，油缸的要求会有较大的降低。

4 旋转连接接头的力学仿真

为了简化力学分析中的几何模型，集合模型只有一组旋转立柱和一组车辙。模型在Solidworks中建立。为了考虑到模型的安全，模型的应力计算是以10s完成旋转的最大的角速度或者最大速度为力学计算的条件。在网格划分时，在零件接触表面能够共用节点，不用建立接触，这样可以减小计算量。车辙旋转连接块和车辙之间的接触设置为绑定模式，旋转接头与车辙旋转连接块之间的接触设置为摩擦，摩擦系数设置为金属摩擦常用的系数：0.18。立柱的底部和顶部都设置为固定，模拟车身和旋转顶板对立柱位移的限制作用。立柱和旋转接头材料采用30CrMnSiA，旋转连接块的材料采用DB685，车辙材料为铝合金。在实际情况中，垫块的材料也是DB685，为简化模型采用铝合金。

首先计算仅在重力作用下，旋转接头的受力大小。在荷载中添加初始重力荷载。仿真计算结果如图10所示。

图10 重力作用下模型部分仿真计算结果

从应力云图10中可以看出，仅重力作用下，模型受力最大处为下部旋转接头与立柱连接处，大小为500.6 MPa。最大位移为9.426 mm。两节桥跨整体质量为1 400 kg，则产生切向加速度的惯性力大小为400 N，远小于重力的大小。当模型在重力和切向加速度双重作用下时，模型的最大等效应力为182.35 MPa，出现在下部旋转接头与立柱相连接的位置。其最大位移达到了11.605 mm。当模型在重力和速度双重作用下时，模型的最大等效应力为500.02 MPa，出现在下部旋转接头与立柱相连接的位置，其最大位移达到了11.305 mm。

当3种荷载同时作用，模型的最大等效应力为482.32 MPa，同样出现在下部旋转接头与立柱相连接的位置，最大位移为12.415 mm。四种不同荷载作用情况下，各构件的最大等效应力见表2所示。

表2 不同荷载组合下各构件的最大等效应力 MPa

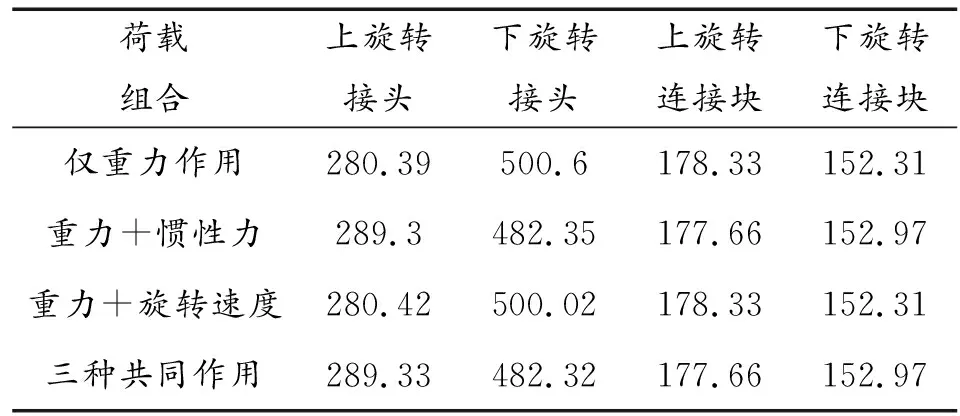
从表2的数据中可以看出，重力作用以外的荷载对旋转接头和旋转连接块的受力影响不是很大。桥跨结构的旋转速度对受力几乎没有影响，但当桥跨存在加速度时，下旋转接头的力减小，上旋转接头的力增加，一定程度上使受力更加均匀。之前计算时的加速度为0.05 m/s2，再分别计算0.1，0.15，0.2和0.25 m/s2时车辙的受力，探究在重力的基础上，旋转的加速度对于车辙桥跨受力的具体影响，计算结果如表3所示。

表3 不同加速度各构件的最大等效应力 MPa

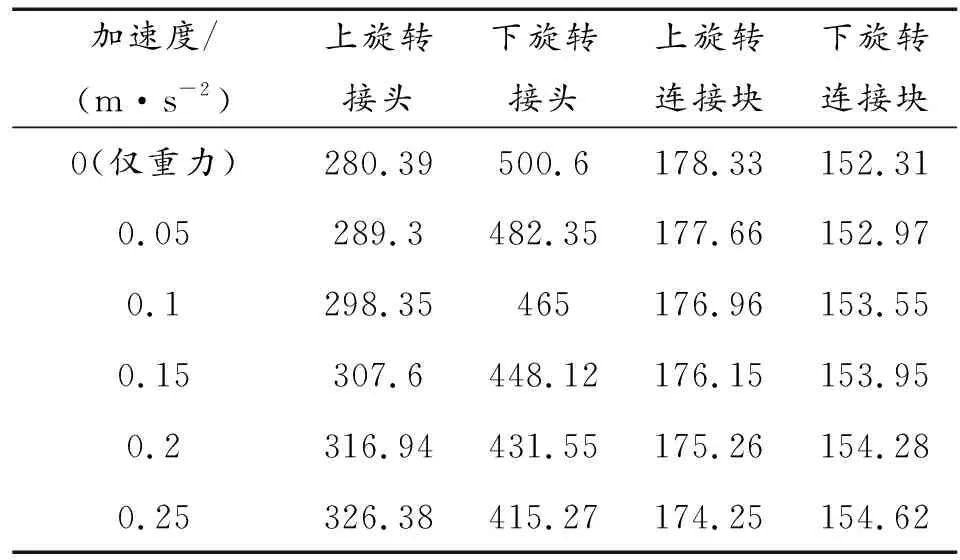
从表3中可以看出，在重力作用的情况下，随着加速度的增大，上下旋转接头与上下旋转连接块的受力趋于一致。仅在重力作用时，上旋转接头主要受到竖向的剪切和轴向的拉力。拉力主要是车辙的重力产生的弯矩造成的。下旋转接头主要受到竖向的剪切和轴向的压力。当车辙存在加速度时，车辙的纵向与水平方向的夹角变小，一定程度上使得上下旋转接头在各自轴向上的受力变得一致，所以其受力也更加一致。但从这个角度考虑，旋转架设的时间应该越短越好。