基于二维切片的同态滤波实现三维图像增强

李媛淼，孙华燕，郭惠超

(航天工程大学 电子与光学工程系, 北京 101416)

基于距离能量原理的激光三维重建技术思想最早由法德圣路易斯研究院(French-German Research Institute of Saint-Louis)的Martin Laurenzis等[1]为提高成像速度而提出，通过利用高质量的矩形激光脉冲和距离选通门来获得距离-能量的关系，从而至少只需要2幅二维切片即可得到一幅三维图像。这种方法有效的减少了需要处理的像素数据量，解决了传统“切片式”三维重建数据量大的困难。为了有效利用获取到的强度信息并提高成像精度，2011年，张秀达等[2]提出基于三幅时间切片的指数编码体制，并将这一理论应用于实验中。2014年，中科院半导体研究所[3]提出了基于三角形距离能量相关算法的编码超分辨率三维成像，实现了三幅切片图像7码道超分辨率成像。以上方法基于原始数据在三维成像的距离精度上做出了很大贡献，但由于激光成像的过程中受到各种因素影响，使得采集到的激光图像被噪声的污染，导致三维重建结果的人眼可视化效果往往不及强度图像。激光主动图像中的噪声主要包含高斯噪声和散斑噪声[4]，其中噪声的主要成分为近似于乘法模型的散斑噪声[5]。抑制激光主动图像中的散斑噪声的方法包括基于空域滤波的传统降噪法、变换域(频率域滤波、小波滤波等)降噪法以及基于硬件系统优化结合后期图像处理的降噪法。传统降噪法使用条件受限，效果不明显[6]；变换域降噪能够去除多种散斑噪声，实现目标与噪声分离的同时保护目标区域边缘信息和结构信息。以上降噪方法均可抑制二维图像的散斑噪声污染，提高二维图像的分辨率、清晰度，但也在一定程度上改变了二维图像像素信息的分布。本文针对目前得到广泛实践的基于三角形距离能量相关算法对二维切片中原始像素信息的需求，将频域滤波中具有代表性的同态滤波算法应用于二维切片序列的降噪中，实现在三维重建中确保三维信息准确性的同时完善三维图像细节信息，提升三维图像可视化效果。

1 基于距离能量的三维成像

1.1 成像过程

基于距离能量的三维成像与传统的通过二维切片序列堆叠的“切片式”三维成像不同，这一方法利用高质量的矩形激光脉冲和距离选通技术获得距离与接收光强的关系，从而至少需要两幅二维切片即可获得三维信息。

理想的成像过程：计时器开始时，脉宽τp的矩形激光脉冲照亮目标区域，距离选通门经延迟时间τD,N后开始对回波信号进行接收，距离选通门门宽为τg，通过距离选通门的回波信号生成第N张二维切片，这一过程即为一个成像周期。通过改变延迟时间τD,N可得到一系列二维切片，图1显示了相邻两个成像周期(N=1,N=2)的时序图。

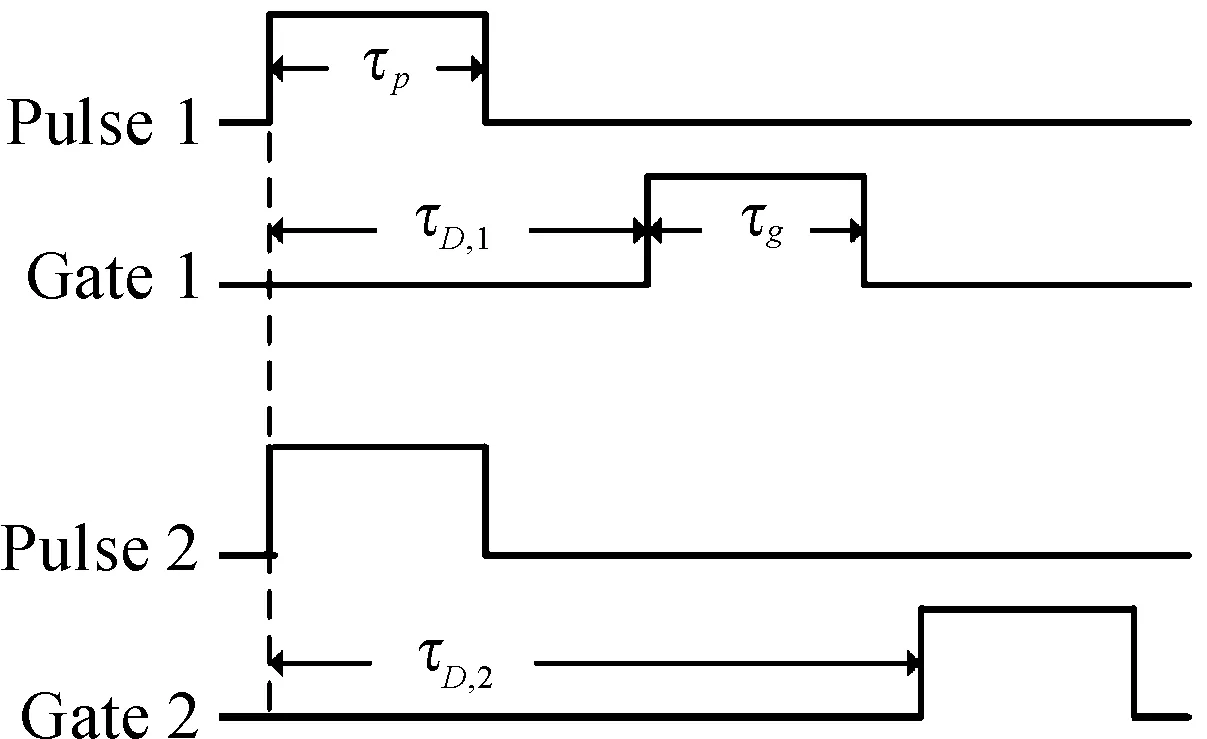
图1 门选通成像时序图

1.2 距离公式

在一个成像周期内，通过距离选通门的回波信号能量表示为

(1)

其中P(t)为矩形激光脉冲函数，G(t)为矩形距离选通门函数。二维切片的像素灰度值L(z)与回波信号的强度Q(z)为正相关，因此，二维切片的灰度值分布可以用来表示距离选通门接收的回波信号能量。为便于计算，引入函数I(z)，表示生成二维切片时，实际可积分的回波能量与可积分的最大能量之比[7]，即对通过距离门的回波信号能量进行归一化，进而得到与距离信息相关的能量包络，表达形式为

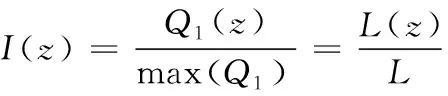
(2)

L为二维切片图像的最大灰度值，I(z)的最大值Imax=1，这一函数称为距离能量分布函数(Range-Intensity Profiles,RIP)[8]，当τp=τg时，函数包络形如图2所示。

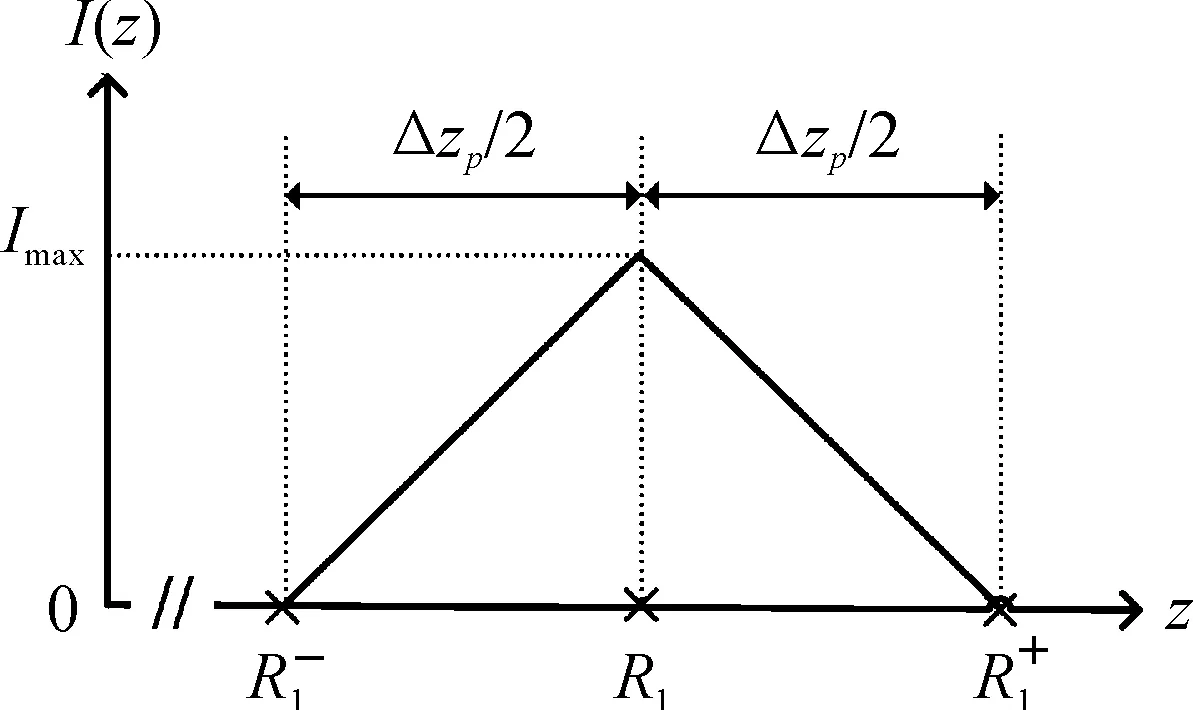
图2 三角形距离能量分布函数包络形

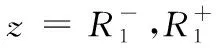
τD,2-τD,1=τp

(3)

的两个成像周期的距离能量分布函数获取距离信息，这两组成像周期的距离能量分布函数I(z,1)、I(z,2)如图3所示。

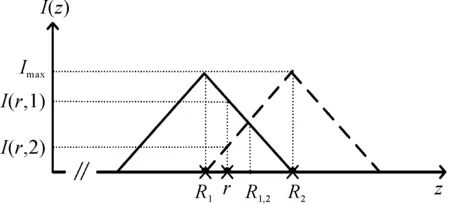
图3 用于获取距离信息的两组距离能量分布函数

令：

(4)

(5)

分别表示第一张二维切片RIP下降沿、第二张二维切片RIP上升沿包含的距离-强度信息。通过两张二维切片图像，可得到待求距离信息r(r∈[R1,R2])为

(6)

2 同态滤波

2.1 同态滤波

在图像入射-反射模型中，图像可由入射分量i(x,y)与反射分量r(x,y)的乘积表示，表征形式为

f(x,y)=i(x,y)r(x,y)

(7)

通常情况下在空间域，入射分量变化缓慢，反射分量会在目标分界处引起突变。根据式(7)的表征形式，实现空间域中乘性噪声的滤除并不容易。

同态滤波是将乘性噪声转化为加性噪声并抑制噪声的滤波方法，该过程通过同时压缩灰度范围和增强对比度来改善一幅图像的表现。图4对一般意义上的同态滤波流程进行了描述。

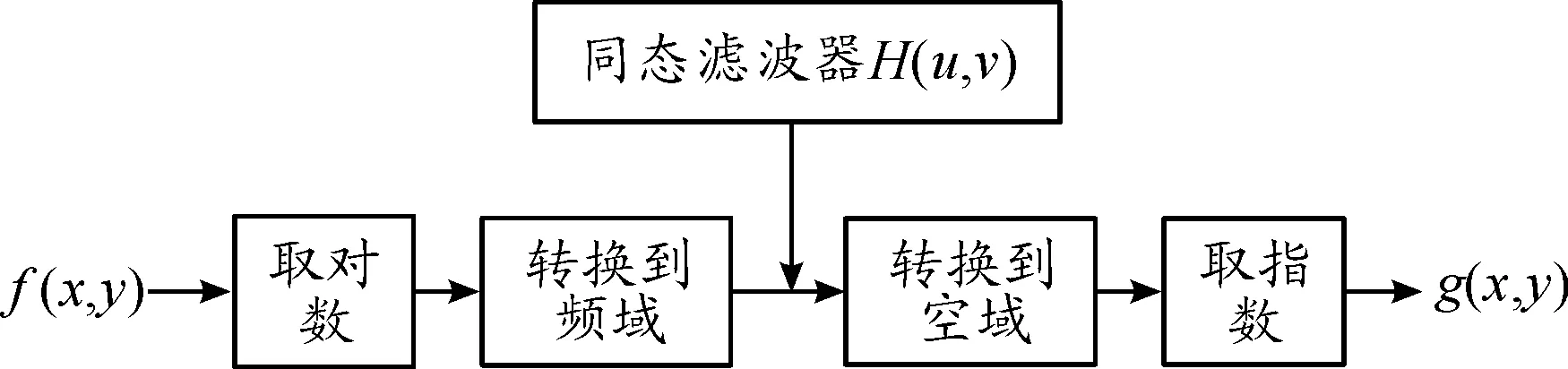
图4 同态滤波流程

激光主动成像生成的二维切片序列中，反射分量r(x,y)中包含以高频形式存在着的目标的边缘信息、结构信息，以低频形式存在的平面目标的平滑区域信息；入射分量i(x,y)中主要为低频形式存在的背景噪声等[9]。为完善三维图像细节信息，提升三维图像可视化效果，需去除低频分量保留高频分量，从而实现背景噪声与目标的有效分离。

2.2 高通滤波器的设计

根据上述滤波的目的，应设计高通滤波器H(u,v)进行降噪处理。考虑距离能量三维成像的特殊性，为更好的保持图像的原始灰度，选取传统的同态滤波增晰法[9]。目前，频率域内常用的传统高通滤波器有高斯型高通滤波器、二阶巴特沃斯型高通滤波器、指数型高通滤波器[10]，表达式分别为

高斯型高通滤波器(GHPF)：

(8)

二阶巴特沃斯型高通滤波器(BHPF)：

(9)

指数型高通滤波器(EHPF)：

H(u,v)=(γH-γL)e-c(D0/D(u,v))2+γL

(10)

对于高通滤波的高频增益γH>1，低频增益γL<1，锐化参数介于高频增益与低频增益之间。D0为截止频率，由于激光主动图像的频域范围较窄，经大量实验，针对本文的激光主动图像，D0值的选取在区间[3,6]较为合适。

本文通过将同态滤波引入基于距离能量的三维成像中，用来提升三维成像质量。算法的流程如图5所示。

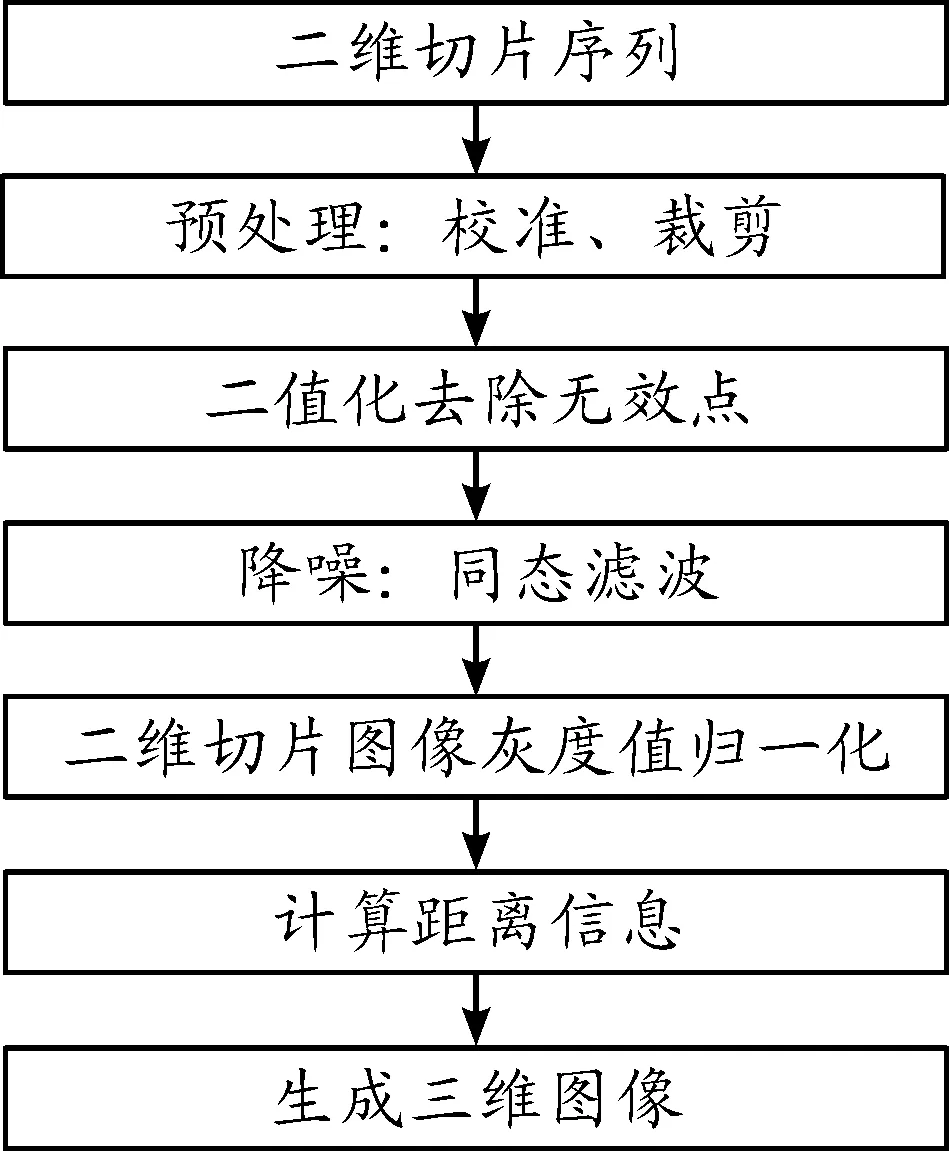
图5 基于两张二维切片的三维重建流程框图

3 实验与分析

3.1 二维切片质量

选取文献[11] 针对距离约500 m楼房的成像实验中的一组二维切片[11]，距离选通门的门宽与激光脉冲脉宽均为100 ns，选取延时步进为100 ns[满足本文式(3)的条件]的两张二维切片，有效距离深度15 m，进行基于距离能量的三维重建。选取的两张原图切片如图6(a)所示。分别采用式(8)、式(9)、式(10)的3种同态滤波器，并选择可以有效增强图像可视化的参数进行滤波处理，具体实验参数如表1所示，图6(b)为在选取参数(1)的高斯型同态滤波后的两张二维切片结果。

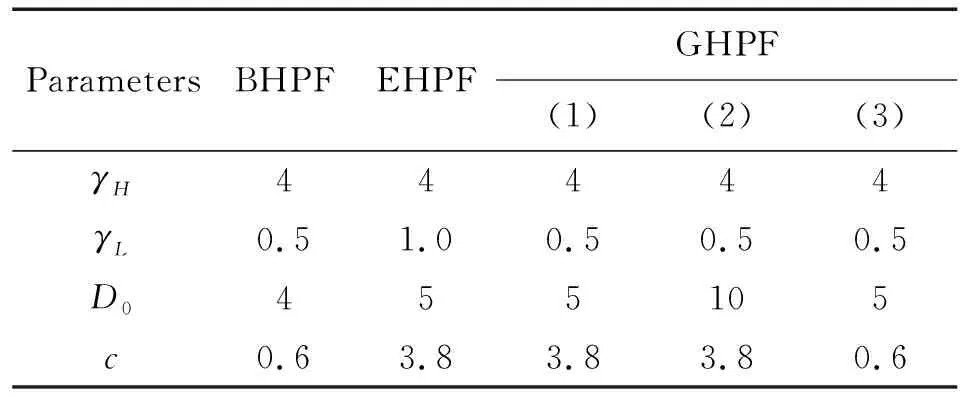
表1 实验参数

图6 原始切片序列与高斯滤波后的切片

皮尔森相关系数(Pearson correlation coefficient)可用于反映两个变量的线性相关程度。根据距离信息计算可知，I(r,1)与I(r,1)+I(r,2)的相关性将直接影响距离信息的计算[12]。将皮尔森相关系数用于评价二维切片的滤波后质量，具体的计算步骤为

1) 分别提取两张二维切片第n行，包含有距离信息的区间[a,b]的灰度值，即选取第n行第a列至第n行第b列的两组灰度值(m=b-a+1)，表示为

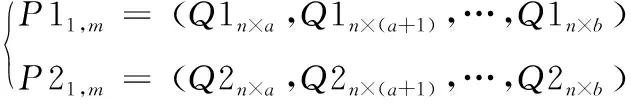
(11)

2) 根据提取到的两个行向量，计算第n行数据的相关性，SCOCC的计算公式为

(12)

选取切片序列中第270行90列至325列(目标主要为墙面，因此反射率在这一区间可视为相等)、380行90列至325列(目标中包含有玻璃部分，其反射率与墙面相差较大，因此反射率在这一区间存在较大变化)作为待计算的行向量，具体位置如图6(a)所示。计算未经滤波的原图、经二阶巴特沃斯型同态滤波器滤波后的图像、经指数型同态滤波后的图像、经高斯型同态滤波后图像的皮尔森相关系数，列于表2中。

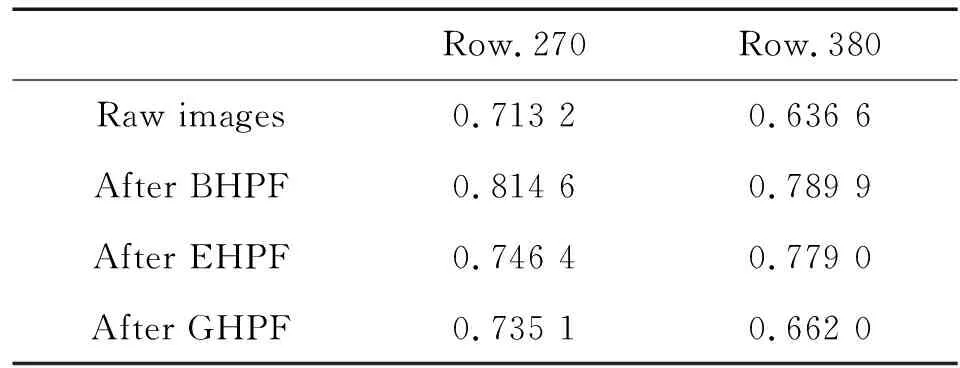
表2 原图与3种滤波后图像行的皮尔森相关系数

4组数据的取值均在0.6～0.8，均为强相关。在成像过程中，由大气湍流、背景噪声和传感器引起的噪声是随机的，因而不具有相关性。经滤波后的3组图像，线性相关程度均比原图有所提升，这一结果验证了同态滤波可有效分离噪声的结论。

在基于距离能量进行三维重建的过程中，二维切片图像中像素点的灰度值用于三维重建中距离信息的计算，因此为保证距离信息恢复的准确性滤波前后目标区域的灰度值大小不应有过大变化。本文采用峰值信噪比(PSNR)用来描述处理后图像与原始图像的相似程度、衡量图像失真情况。计算公式为最大可能功率与破坏性噪声功率的比值，对于区域大小为M×N的表达式为

(13)

L为二维切片图像的最大灰度值，在本文中L=255。使用不同的采样率计算3种同态滤波后图像的峰值信噪比，切片一与切片二的计算结果分别如图7(a)、图7(b)所示。根据计算结果，指数型同态滤波、二阶巴特沃斯型同态滤波对原始图像灰度信息有较优的保留能力，而高斯型同态滤波后的图像灰度值的失真情况较前两者严重。

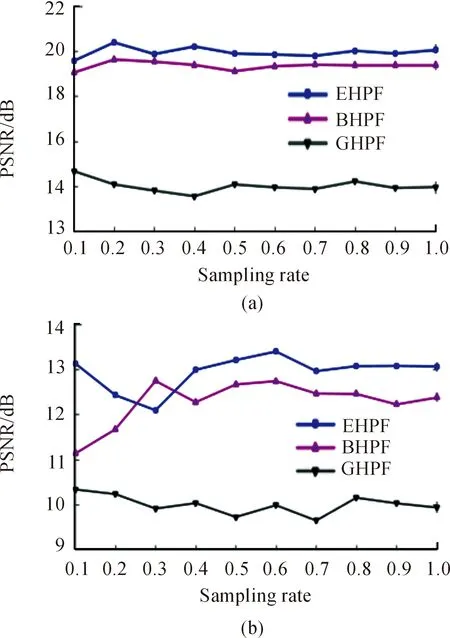
图7 PSNR计算结果

将3种方法滤波后的(第270行)I(r,1)+I(r,2)值进行对比，如图8所示。经高斯型同态滤波后的图像，对包含有目标区域的增强效果更好，较大的提升了目标区域的灰度值，实现了与背景噪声和无效点的有效分离。

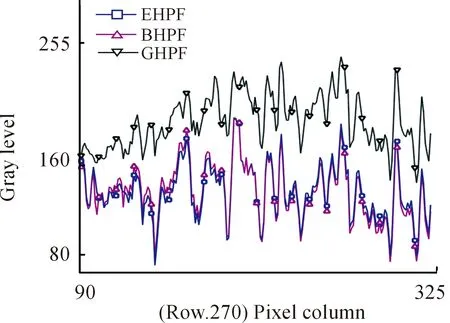
图8 3种方法I(r,1)+I(r,2)灰度值

3.2 同态滤波对三维图像的距离精度的影响

将未经处理的切片序列与同态滤波后的切片序列进行重建，重建结果如图9所示。在有效的距离深度15 m范围内，采用原始图像的重构结果距离深度被压缩至约8 m，滤波后的3组切片序列重建结果保留了约11 m的距离信息，距离分辨率小于1 m。

(b)(c)(d)(e)(f)分别对应采用表1参数的三维重建结果

图9 三维重建结果

通过结合强度图像的信息，可以看出，同态滤波后的三维重建图像细节信息更加明显。例如，左上楼房顶角部分由于激光照射不足，在使用原图重建时，这部分的信息没有得到恢复，在经同态滤波消除激光照射区域受限的影响后，左上信息得以恢复，其中GHPF在参数(1)的情况下重建效果较优；楼房主体部分的窗户区域具有材质多(导致反射率不均匀)、面积小、间距小的特点，在原图的重建过程中窗户区域的细节信息极为模糊，可视化效果较差。同态滤波后，窗户区域的细节基本得以重建，其中BHPF的重建效果较优。从整体情况来看，滤波后的图像均匀度下降，出现大量明显的无效点。

同样取第270行区间AB的三维重建数据比较各种方法的距离精度[11]，滤波后的重建结果比较如图10所示，数据均匀度较好的是采用GHPF的数据，这一结果与观察图9得到的结果是一致的。

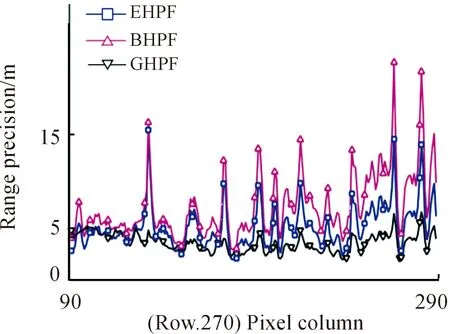
图10 3种方法的距离精度

取GHPF滤波后的三维重建数据与原图的三维重建数据，如图11所示。原图重建的三维数据突变值小，数据的稳定度更好，经GHPF滤波后得到的三维重建数据突变值更多且数值较大，这样的数据分布情况导致了滤波后重建图像的均匀度下降。

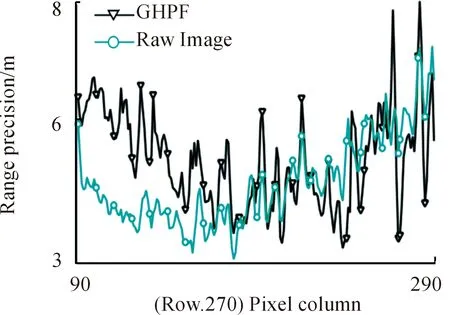
图11 原图与GHPF滤波后三维成像的距离精度

4 结论

基于距离能量的三维成像与传统的“切片式”三维成像相比所需数据量更少，在远距离、大景深目标的三维成像中具有很大的优势。本文将同态滤波应用于二维切片序列的滤波降噪处理过程中，通过应用到实际图像的处理，验证了同态滤波能偶在保证一定距离精度的条件下，有效减少由于激光照明不均匀、大气散射与背景杂散光引起的噪声，并有效完善了三维重建图像细节信息，提升了三维图像的可视化效果。这一应用能够为人眼有效识别目标类型、消除目标本身反射率不均匀的影响提供指导方向。同时，经同态滤波后重建的三维图像均匀度较差，存在大量无效点，后续将就三维图像均匀化问题、研究保证距离精度的同时增强三维图像的算法。