2018年天津市中考网格作图题的多角度探究

（天津市东丽区教师进修学校；天津市河东区教育中心）

天津市近几年数学中考的网格作图题从静态图形的作图问题，已经发展到结合图形变换的作图问题.笔者通过对2018年天津市中考试卷第18题的命题立意、几何原理、解法剖析等方面进行研究，感悟到此题承载了给学生提供经历观察、实验、猜测、计算、推理、验证等活动过程，叹服于命题人的匠心独运.下面笔者从不同角度对此题进行探究，并仅以此与读者共享.

题目如图1，在每个小正方形的边长为1的网格中，△ABC的顶点A，B，C均在格点上.

（1） ∠ACB的度数为_____；

（2）在如图所示的网格中，P是BC边上任意一点.以点A为中心，取旋转角等于∠BAC，把点P逆时针旋转，点P的对应点为P′.当CP′最短时，试用无刻度的直尺，画出点P′，并简要说明点P′的位置是如何找到的（不要求证明）.

图1

这是一道将基本几何图形放置在网格中，将图形绕某定点旋转，并研究满足一定条件的对应点位置的作图题.题目将图形变换基本思想与网格作图有机融合，是一道培养学生思维、开启学生智慧的好题.下面从几个方面加以研究.

一、思细理，变换之中自有深意

这道题的几何模型源于人教版《义务教育教科书·数学》七年级下册第五章“相交线与平行线”中的“垂线段最短”.剥离开旋转看这道题，即为：若P为线段BC上的一个动点，D为线段BC外的一个定点，则当PD取得最小值时，确定点P的位置及线段PD的长度.

将一个简单的几何原理增加了旋转的因素后，凸显出了动态观点下解决问题的思维品质，能够充分展现学生运用已有的学习经验解决问题的能力.

要解决这个问题，首先需要确定解决问题的策略.根据旋转的性质，可以将题目分成两个不同的方向.为研究问题的方便，我们给出如下引理.

引理：如图2，在△ABC中，∠ACB=90°，P为边BC上一个动点，以点A为中心，取旋转角等于∠CAB，将点P逆时针旋转，点P的对应点为P′.

（1）若将△ABC也作同点P一样的旋转得到△AB′C′，则边B′C′为点P′运动的轨迹；

（2）若AB边上的一个定点D满足AD=AC，则当DP⊥BC时，CP′取得最小值，且该最小值等于线段PD的长度.

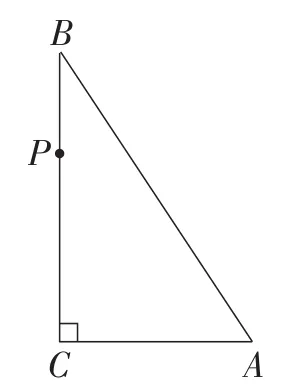
图2

证明：（1）如图3，取旋转角等于∠CAB，将△ABC绕点A逆时针旋转得到△AB′C′.因为点P在边BC上，所以其对应点P′一定在边BC的对应边B′C′上.因为P为边BC上一动点，所以点P′的运动轨迹为边B′C′.

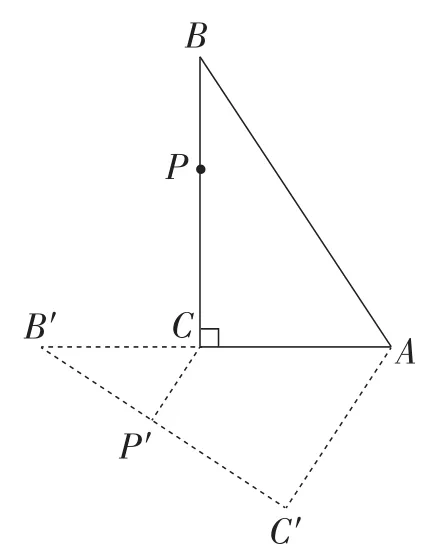
图3

图4

（2）如图4，连接PA，以点A为中心取旋转角等于∠CAB，将△APD逆时针旋转，由AD=AC，故得△AP′C.由旋转得△PAD≌△P′AC.从而得P′C=PD.因为点D为定点，显然当DP⊥BC时，DP最小，此时CP′也最小，这个最小值就是当DP⊥BC时PD的长度.

从上面的分析可以看出，2018年天津市网格作图题蕴含着极其丰富的几何变换的数学原理，一方面，是在“动中寻矩”；另一方面，是在“变中求恒”，弄清楚这其中的几何道理，是破解这一网格作图题的第一步.

二、研解法，网格构图大显神奇

1.借助网格的几何特性构图

（1）动中寻矩.

按照“动中寻矩”的思路，题目中确定点P′的关键是确定点P′的运动轨迹，即只需要作出边BC绕点A逆时针旋转得到的边B′C′.根据旋转前后图形全等的特点，由引理（1）可知，借助△AB′C′≌△ABC的想法更容易作出边B′C′.

为了更好地理清△AB′C′的网格作图方法，我们先提出如下问题：若取旋转角等于∠CAB，将△ABC绕点A逆时针旋转得到△AB′C′，如何借助网格画出△AB′C′？

下面我们给出两种不同的思路.

思路1：虚格点构图法.

如图5，考虑到点C′一定满足∠C′AC=∠BAC，于是点C′一定落在线段AB关于直线AC对称的对应线段AK上.要作出点C′，我们需要作出线段AK.但实事上，此时的点K落在了给定的网格区域外，为准确找到点K，可以取格点T，E，H，I，分别作线段TE，HI的延长线，它们的交点就是点K，连接AK.取格点B′，下面要过点B′作线段AK的垂线.取格点D，G，M，N，线段DG，MN的延长线相交于点F，连接B′F，B′F与AK相交于点C′，则△AB′C′即为所求.

图5

若两条格点线段的延长线在给定网格区域外相交，且交点恰好为与原网格相匹配的某一格点的位置，那么我们不妨称这个位置为“虚格点”，如图5中作出的点F和点K.

网格作图问题必须都是要在给定网格区域内完成的，但是为了作图或研究问题的方便，有时我们需要借助原有网格中的格点，以及这些格点所具有的内在的数学逻辑关系，构造出我们需要的虚格点.这里给出的作虚格点的方法是准确作图，可以视为作辅助线或辅助点.

思路2：格点缩进构图法.

在虚格点构图法中，我们构造了虚格点K，F，最终作出了点C′，得到了△AB′C′.在作图中我们发现，线段B′F与AK分别经过了两个小正方形的中心，所以这里给出如下新的作图思路.

如图6，连接小正方形TRFS与EMDN的对角线，交点分别为点G，J，取格点B′，连接AJ，B′G并延长，相交于点C′，从而得到△AB′C′.

图6

当我们要在网格中画一条线，而又觉得网格的区域不够使用时，可采取先确定这条线上的特殊点（如一个小正方形的中心），再把这个特殊点和其中容易确定的端点（格点）连接起来即可，这种方法我们不妨叫做格点缩进法.

（2）变中求恒.

按照“变中求恒”的思路，对于点P′的确定，事实上存在两种不同的解决策略.

思路1是在作出B′C′的基础上，考虑过点C向线段B′C′作垂线，垂足即为点P′；

思路2是在作出B′C′的基础上，先利用引理（2）确定点P，进而确定点P分线段BC所成的比，再利用比例作出点P′.

下面分别给出基于这两种不同策略下的作图方法.为叙述起来方便，下面求作点P′的作图过程，都假设已经作出了△AB′C′，即作法中均省略作△AB′C′的过程.

思路1：根据前面的引理知道点P′一定在线段B′C′上，只需过点C作B′C′的垂线，垂足即为点P′.

作法：如图7，取格点T，S，连接TS交AB于点L，连接LC并延长，交B′C′于点P′，点P′即为所求.

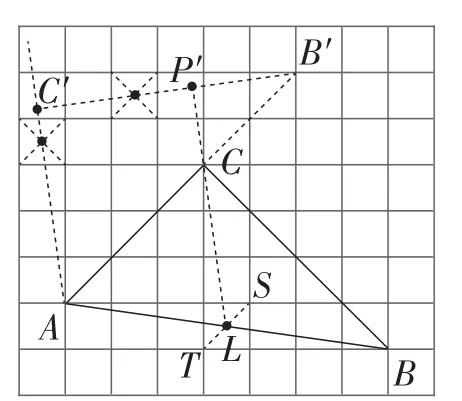
图7

图8

思路2：如图8，取AB边上的点D，使得AD=AC.由引理知，当DP⊥BC时，DP的值最小，即CP′的值最小，这个最小值就是当DP′⊥BC时PD的长度.由题意有BD∶DA=B′P′∶P′C′=2∶3.故只需在线段B′C′上作出满足B′P′∶P′C′=2∶3的点P′即可. 同时，因为可得

作法1：如图9，取格点E，D，M，连接ED，AM，它们相交于点F，连接FC并延长，与B′C′相交于点P′，则点P′即为所求.

作法透析：

由作图得MF∶FA=DM∶AE=2∶3，B′C∶CA=2∶3.

又因为AC′∥FC∥B′M，

所以B′P′∶P′C′=2∶3.

故点P′即为所求.

图9

图10

作法2：如图10，取格点M，N，连接MN交B′C′于点P′，则点P′即为所求.

这一作图过程看上去非常简洁，但其中蕴含的道理却极其丰富，下面我们给出证明.

作法透析：

如图11，取格点Q，Q′，连接B′Q′，BQ，容易证明△B′Q′A≌△BQA.

所以线段CQ旋转后的对应线段为C′Q′.

因为CQ平分∠ACB，

所以C′Q′平分 ∠AC′B′.

取格点Y，连接B′Y，AY，

由 ∠AC′B′=∠AYB′=90°， 得A，Y，B′，C′四点共圆.

又因为YA=YB′，

所以线段C′Y平分∠AC′B′.

所以C，Q′，Y三点共线.

因为Q′Y∥MN，B′P′∶P′C′=B′N∶NY=2∶3，

所以点P′即为所求.

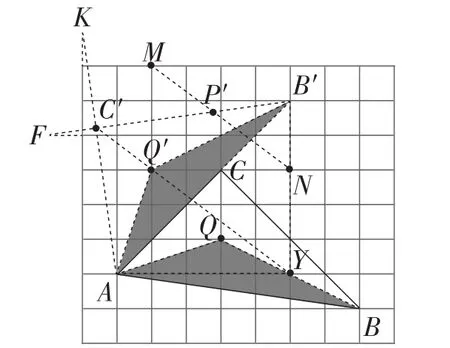
图11

按照思路2，此题还可以有其他作法，在此不再赘述.

此题亦可借助网格的坐标特性，先求出点P′的坐标，再通过构图确定点P′的位置.

三、究延伸，拓展之后风光无限

抛开网格，我们将问题进一步研究，可得到如下拓展推论.

拓展：如图12，在△ABC中，∠ACB=90°，BC=a，AC=b，AB=c，P为边BC上一动点，以点A为中心，取旋转角等于α，且满足∠CAB+α=180°，将点P逆时针旋转，点P的对应点为P′.

（1） 若将△ABC也作同点P一样的旋转得到△AB′C′，则边B′C′为点P′运动的轨迹；

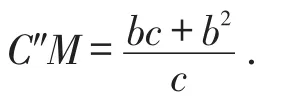
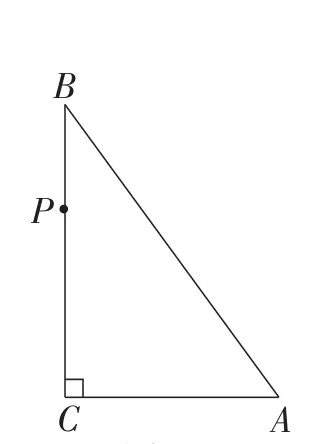
图12

图13

证明：（1）如图13，取旋转角等于180°-∠CAB，将△ABC绕点A逆时针旋转得到△AB′C′.

因为点P在边BC上，

所以其对应点P′一定在边BC的对应边B′C′上.

因为P为边BC上一动点，

所以点P′的运动轨迹为边B′C′.

（2）在图13中，连接PA，P′A，CP′，C″P，

由题意，得∠PAP′=∠CAC′，

即∠PAC+∠CAP′=∠P′AC′+∠CAP′.

所以∠PAC=∠P′AC′.

又因为点C″为点C′关于直线AC的对称点，

所以∠C″AO=∠C′AO.

又因为 ∠PAC″=180°-∠PAC-∠C″AO， ∠P′AC=180°-∠P′AC′-∠C′AO，

所以∠PAC″=∠P′AC.

又由题意有PA=P′A，AC=AC′.

因为点C″为点C关于直线AC的对称点，

所以AC′=AC″=AC.

所以△PAC″≌△P′AC.

所以CP′=C″P.

因为点C″是定点，

所以当C″P⊥BC时C″P的长度最小，即CP′的最小值等于C″M.

因为点C″为点C′关于直线AC的对称点，

所以OC″=OC′，C″M⊥BC.

所以C″M∥CA.

所以AT=AC′=AC=b.

下面给出2018年天津市中考试卷第18题的一个变式.

变式：如图14，是由边长为1的小正方形组成的网格，点A，B，C均为格点.若P为边BC上一点，以点A为中心，取旋转角等于α，且α+∠CAB=180°，将△ABC逆时针旋转，点B，C，P的对应点分别为点B′，C′，P′.

（1）画出△AB′C′；

（2）当CP′最小时，画出点P′，并简要说明你是怎样找到点P′的.

图14

图15是该变式的一个答案，其构图思路与作法可效仿前面的思路与作法.

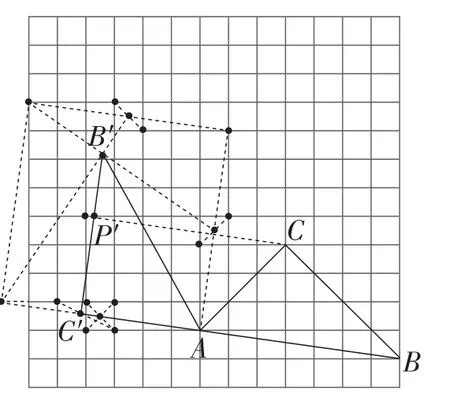
图15

四、品物化，核心素养落地生根

《义务教育数学课程标准（2011年版）》要求：通过对有关问题的探讨，了解所学知识（包括其他学科知识）之间的关联，进一步理解有关知识，发展学生的应用意识和能力.

此题中，在寻求点P′轨迹的过程中，需要沟通三角形、旋转及全等三角形等相关的内容；在确定点P′位置的过程中，还需要进一步沟通“垂线段最短”等内容.这些需要沟通的内容对学生来讲是耳熟能详的，而把这些内容综合在一起，在不同于寻常的解决几何问题环境的网格中，以“确定点P′的轨迹及点P′的位置”为目标，从不同的角度进行切入，构建思维起点.

灵活运用所学知识及方法，形成思维去向，进而实现用不同的策略解决问题，这种探究和解决问题的过程其实正是数学核心素养在日常教学中的落实与物化.