一道中考压轴题的拓展

（湖北省武汉市第一初级中学）

2017年湖北省武汉市中考试题第24题是以抛物线为背景的综合题，此题的第（2）小题研究了两条直线的位置关系，直线与抛物线的结合浑然天成，蕴含着数学的自然之美.本文将对此题做以拓展，得出一个与抛物线相关的几何性质，并将该性质应用于数学题目的编写中.

一、试题呈现

题 目已知点A(-1，1)，B(4，6 )在抛物线y＝ax2＋bx上.

（1）求抛物线的解析式.

（2）如图1，点F的坐标为(0，m)(m＞2)，直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为点H，设抛物线与x轴的正半轴交于点E，连接FH，AE.求证：FH∥AE.

（3）略.

图1

二、分析与解答

第（1）小题中，抛物线解析式中的两个基本量a和b，由条件中两个已知点确定，考查学生求函数解析式的最核心、最基本的技能——待定系数法.

解：因为点A(-1，1)，B(4，6 )在抛物线y＝ax2＋bx上，

在第（2）小题中，点E是抛物线与x轴的交点，属于抛物线上重要的特殊点之一，AE是定直线；点F是y轴上的动点，它的运动使得直线AF绕点A旋转，直线AF的旋转改变了它与抛物线交点G的位置，而点H则是动点G在x轴上的正投影，点F和点H的共同运动决定了直线FH的运动方式.

从结论看，直线AF的旋转运动通过抛物线这个桥梁的过渡，转变成了直线HF的平移运动，让人联想到机器中机械零件之间巧妙的联动，十分神奇、有趣.

上文描述的图形的变换可以用数和符号来描述，图形中的点与线之间的各种联动反映在数与式上就是代数式的运算.详细的过程可以描述成如图2所示的思维导图.

图2

证明：如图3，过点A作AN⊥Ox于点N，

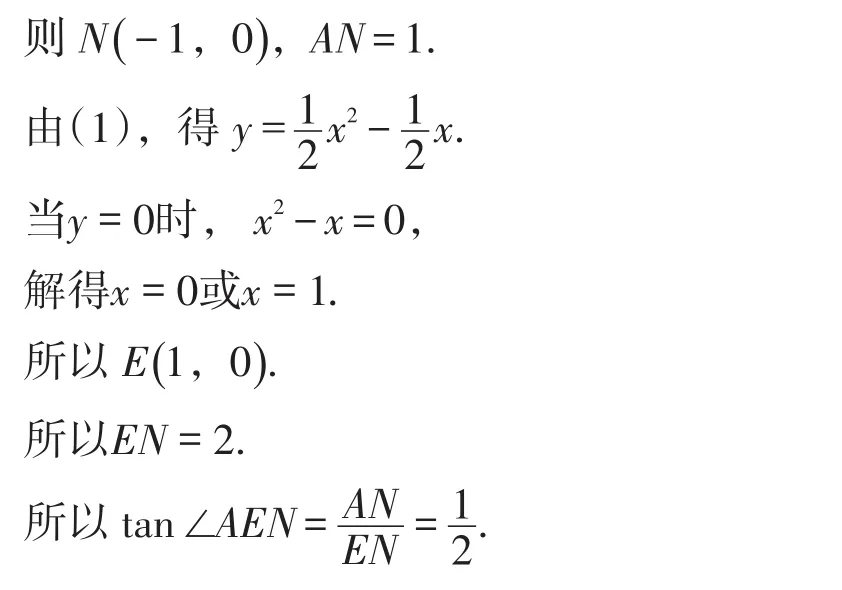
设直线AF的解析式为y=kx+m.

所以∠FHO=∠AEN.

所以FH∥AE.

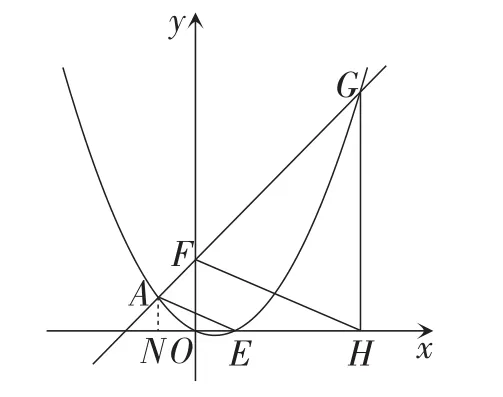
图3

三、更一般的结论

结论：如图4，A，C为抛物线y=ax2+bx+c上任意两点，点B为直线AC上异于点A，C的任意一点，过点B作抛物线对称轴的平行线交抛物线于点E，过点E作BE的垂线交抛物线于点D，过点C作DE的垂线，垂足为点F，则AD∥BF.

图4

显然，上述第（2）小题只是这个结论的一个特例.

不失一般性，我们只证明点B在A，C之间的情形.分两种情况.

情况1：AC∥DE.

如图5，过点A作AH⊥DF于点H，由抛物线的对称性，容易得到HD=EF.所以AB平行且等于DF.所以四边形ABDF为平行四边形.所以结论成立.

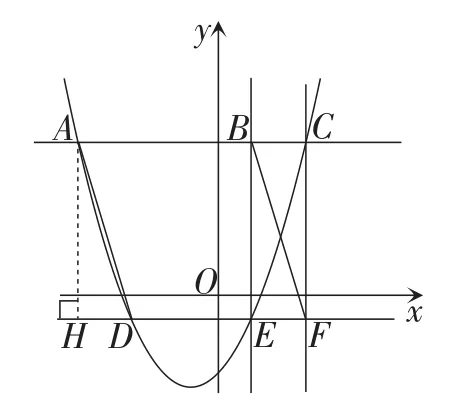
图5

（2）AC与DE相交于点P.

如图6，过点A作AH⊥DF于点H.

设点A，B，C的坐标分别为A(x1，y1) ，C(x2，y2)，B(x3，y3)，直线DE的解析式为y=m.

则可设点E，D，P，F，H的坐标分别为E(x3，m)，D(x4，m)，P(x5，m)，F(x2，m)，H(x1，m).

则可证明AD∥BF成立.

设直线AC的解析式为y=kx+p.

联立抛物线方程与直线AC的方程，得

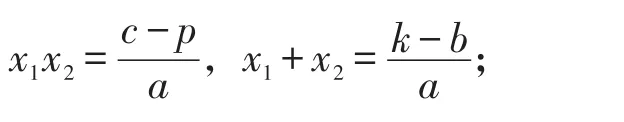
联立抛物线方程与直线DE的方程，得

联立直线AC与直线DE的方程，得

图6

四、编拟相关练习题

利用上述结论，我们可以结合一些具体的、特殊的图形来编拟练习题，作为训练学生思维的材料.

（1）求抛物线的解析式；

（2）B为y轴正半轴上的一个动点，直线AB交抛物线于点C，过点C作CF⊥Ox于点F，求证：BF∥AO.

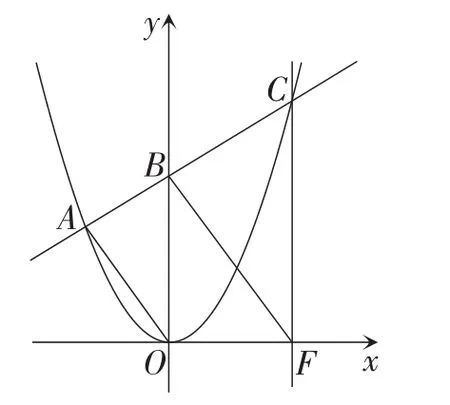
图7

此题将点B放在抛物线的对称轴上，利用坐标轴的特殊地位，将结论中的点D，E整合成坐标原点，使问题特殊化.

我们关注到在点B运动的过程中，∠BFC=30°的结论不变，在此基础上，结合几何图形，我们有比较广阔的编题空间.

练习2：如图8，抛物线y=-x2+3x与x轴相交于点D，直线y=(3-m)x+m2与y轴相交于点B，与抛物线有公共点A.

（1）求证：直线AB与抛物线只有唯一的公共点；

（2）过点A作AF⊥Ox于点F，求证：AD∥BF.

图8

此题将点B放在y轴上，同样巧妙地利用了坐标轴.将直线AB与抛物线相切，公共点重合，将结论中的AH和CF整合成AF，使问题特殊化.

我们关注到此题中△OBF∽△FAD，在此基础上也会有较广阔的编题空间.

以上两个例子是从不同角度将上述结论特殊化，例证了上述结论用于编题的可行性，同时也为我们遍拟相关题目提供了一些思路.

近年来，几乎全国所有地区中考试卷的最后一道试题都是以抛物线为背景的综合题，其中蕴含了大量的几何因素.但仔细研读，发现在很多综合题中，几何部分是硬植入进去的，把抛物线的背景移除，不影响解题.如何将几何图形融入抛物线之中，使综合题浑然一体，是值得研究的课题.