以“点”为核 感悟本质
2021-02-08林志辉朱昭伟
林志辉 朱昭伟

【缘起】
方向和距离是图形平移的两个要素,图形平移是指图形上所有的点都向同一个方向移动了相等的距离,本质上可归结为点的平移,主要特征是对应点之间的连线平行且相等。第二学段的“平移”教学主要是在第一学段整体感受平移现象、直观认识平移的基础上进行再认识。笔者通过前测发现,学生已能较好地辨别平移现象,但对平移的距离是对应点之间的距离的认识不到位,错误地将平移前后图形间的空格作为平移的距离。由此,笔者将“点的平移”作为本课知识技能的核心,促使学生感悟平移的本质特征——“对应点之间的距离相等”,丰厚平移的概念和表象,发展空间观念。教学目标如下。
1.进一步认识图形平移,理解图形平移的特征。能在方格纸上判断一个图形平移的方向和距离,会在方格纸上画出图形按水平或垂直方向平移后的图形。
2.经历图形平移特征的探索、发现过程,积累活动经验,发展空间观念。
3.感受数学知识间的联系,收获成功的体验,激发学习数学的兴趣。
【教学实录】
一、创设冲突情境,初探平移本质
(一)“蚂蚁争吵”,直指核心
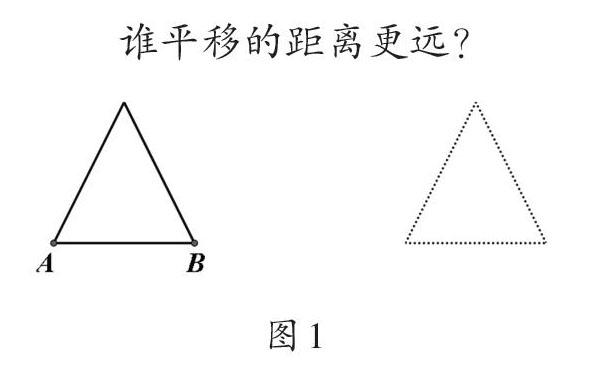
师:一群蚂蚁想把一块三角形的饼干平移到这里。还没开始移,A、B两点的蚂蚁为谁走的路多发生了争吵(如图1)。
谁平移的距离更远?
师:你们觉得呢?
(生争论,回答略)
师:好像说不清楚,你有什么好办法?
生:如果有格子图就方便比较了。
(课件出现格子图)
(二)解决争吵,初感“对应”
师:现在呢?
(生独立思考,小组交流)
生:A点移动10格,B点移动10格,一样多。
(课件演示两点动态平移过程)
师:我们一般把点A移动后的对应点记为点A ',那么点B的对应点就记为点B '。
(设计意图:通过将“两只蚂蚁争吵”的情境引入教学内容,既生动有趣,符合小学生的心理特点,又直指平移的核心——“点的平移”。通过“无格子图”和“有格子图”的对比分析,学生对平移从感性认识逐步走向理性分析。)
(三)明晰“对应”,感悟“等距”
1.再找“对应点”。
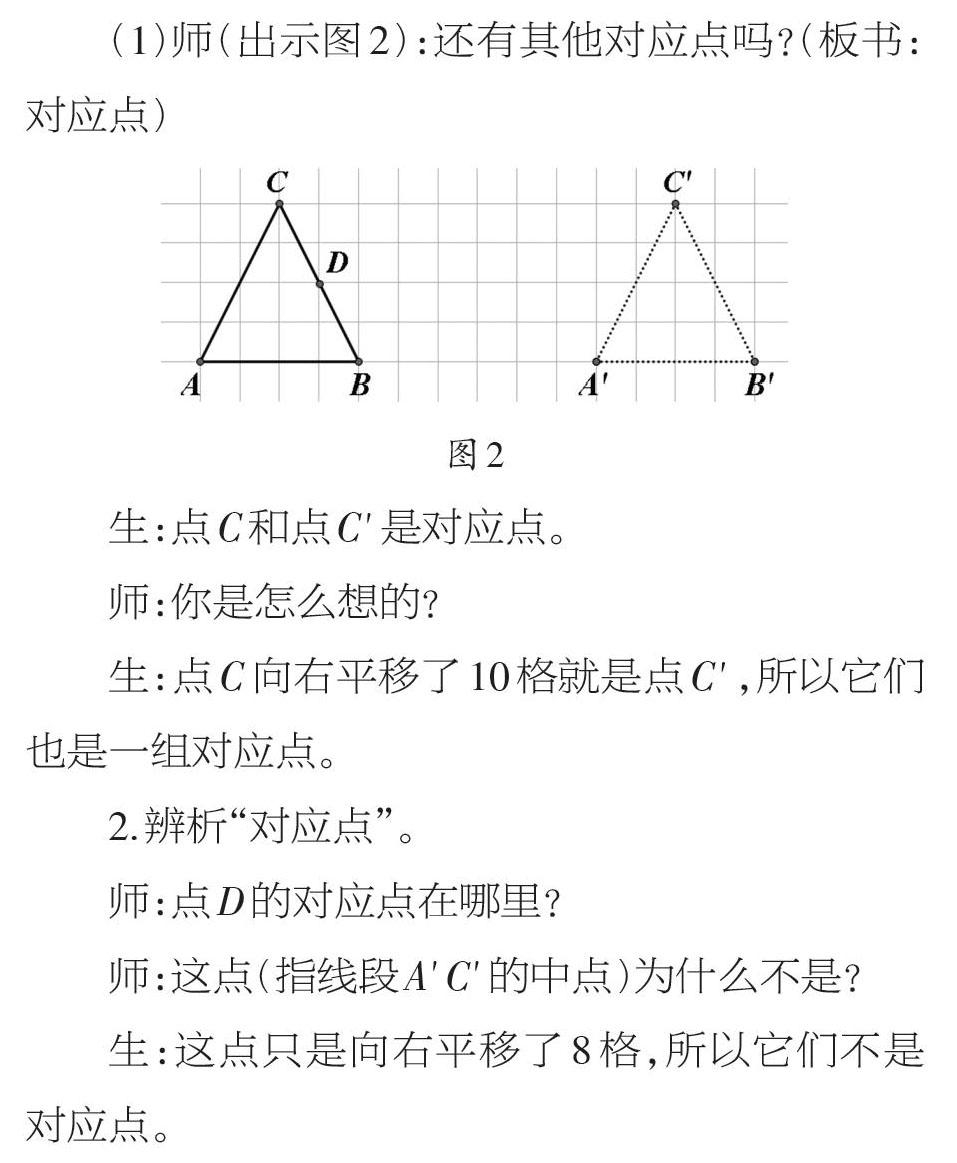
(1)师(出示图2):还有其他对应点吗?(板书:对应点)
生:点C和点C '是对应点。
师:你是怎么想的?
生:点C向右平移了10格就是点C ',所以它们也是一组对应点。
2.辨析“对应点”。
师:点D的对应点在哪里?
师:这点(指线段A 'C '的中点)为什么不是?
生:这点只是向右平移了8格,所以它们不是对应点。
3.观察“对应点”。
(1)师(出示图3):观察每组对应点,你有什么发现?
生:所有对应点之间的距离都是10格,距离相等。
(2)师:是不是所有对应点之间的距离都是10格?(师课件演示)
(3)师(小结):这里所有对应点之间的距离相等,都是10格,也就是这个三角形向右平移了10格。(师板书:距离相等)这节课我们继续来认识平移。(板书课题:平移)
(设计意图:“再找对应点”“辨析对应点”“观察对应点”,从同一层次的正例寻找,到正误例子的辨析,最后到多个对应点的观察归纳,各环节一气呵成又层次分明,指向平移本质,使学生对平移的认识更进一步,为画平移图形奠定基础。)
二、画平移说平移,再感本质
(一)画平移图形
师:还是这个三角形,如果向下平移5格,想一想,怎样画才能又对又快?(生自主尝试后全班交流)
1.展示错例(出示图4)。
师:都是向下平移5格,怎么不一样?
生:图4是把三角形向下平移了9格,而不是5格,从C点到C '点是向下平移了9格。
师:还可以从哪里很快看出是向下平移9格,而不是5格?
生:从点A到点A ',点B到点B '看出。
2.展示正例(出示图5)。
师:这位同学画得又对又快,猜猜看,他是怎么画的?
生:他可能是先找出点C ',再看着形状画出整个三角形的。
生:他可能是先把A向下平移5格找到A ',再把B向下平移5格找到B ',把C向下平移5格找到C ',最后把这三个点用线段连起来。
师:请作品的主人来说说看。
生:我是先把三个点都向下平移了5格,找到对应点,再连上线段。
(师板书:找点、连线)
3.画错的学生自主修正。
4.小结:(课件动态演示)向下平移5格,也就是每个点都向下平移了5格,可以通过“找关键点,再连线段”的方法来完成平移。
(二)说平移
1.初说平移。
师:把这个三角形再向左移动6格,想一想会怎样。(学生说一说,指一指。课件动态演示)
2.多次平移。
师:把三角形A 'B 'C '平移到原来的位置,该怎么平移?(学生说一说,指一指。课件动态演示)
3.小结:对应点帮助我们既能快速“找点、连线”画平移,还能比较容易地说出是怎么平移的。
(设计意图:此環节是本节课的重点,画平移、说平移是密不可分的两个部分。画平移反馈环节的两次展示,既有图像和文字表述,又有正例和错例、一般方法和“找点、连线”方法的对比。说平移环节,层次分明,快速推进,亦算巩固环节。)
三、已知对应点画平移,三悟本质
(一)再画平移图形
师:这是一个直角三角形(出示图6左半边),想象一下,它平移后会怎样?(学生只想象不回答)
师(出示完整的图6):如果这是它平移后三角形的一个顶点,想象一下平移后的图形会怎样。
(二)交流反馈
1.作品1(出示图7)。
师:猜猜看,他是怎么想的?
生:他是把这个点看成B的对应点B ',向右平移了5格,其他点也向右平移了5格,再连上线段。
2.作品2(出示图8)。
师:我这里有个作品写着向右平移了7格,他是不是搞错了?
(师展示作品)
生:他可能是把这个顶点看成A的对应点A ',就应该向右平移7格。
师:一会向右平移5格,一会向右平移7格,为什么都可以?
生:对应点不同。如果它是B ',和B成为对应点,距离是5格,其他点也要向右平移5格,三角形就向右平移5格。如果它是A ',和A成为对应点,距离是7格,其他点也要向右平移7格,三角形就向右平移7格。
3.作品3(出示图9)。
师:还可以怎样?
生:把它看成C ',和点C成为对应点,先向右平移7格,再向下平移4格。
生:还可以先向下平移4格,再向右平移7格。
(三)异中求同,再悟“对应”
师:仔细观察这三个作品(出示图10),你有什么发现?
生:当它是B的对应点B '时,距离5格,三角形都要向右平移5格;当它是A的对应点A '时,距离7格,三角形都要向右平移7格;当它是C的对应点C '时,就要向右平移7格,再向下平移4格。关键看和谁成为对应点。
生:无论这个顶点是谁的对应点,每次平移后,对应点之间的距离都是相等的。
师:如果已知的这个点不是顶点呢?
生:无论怎么平移,对应点之间的距离都相等。
(设计意图:给对应点画平移,是开放的练习设计,学生一次次突破思维定式。从同中求异到异中求同,既发展了学生的创新意识,又时刻指向平移的本质。)
四、课堂小结(略)
(浙江省溫州市滨江外国语小学 325000)
