指向数学核心素养的问题情境策略——以“圆”的教学为例

（浙江省宁波市镇海蛟川书院）

一、问题的提出

什么是情境？裴亚光先生认为，情境就是为了实现教学目标而营造的特定背景，是数学学习、数学思维、数学活动得以产生的具体条件.《义务教育数学课程标准（2011年版）》（以下简称《标准》）中指出，初中生要初步学会在具体的情境中从数学的角度发现问题和提出问题，并综合运用数学知识和方法解决简单的实际问题，增强应用意识，提高实践能力.问题是数学的核心，情境是问题的载体.学生的已有认知准备与面临的问题发生认知冲突就形成了问题情境.在教学中，如何关注知识的发生、发展过程，突出数学主线，凸显数学的内在逻辑联系和思想方法，落实数学核心素养的培养，是我们的当务之急.笔者以浙教版《义务教育教科书·数学》九年级上册“3.1圆”（第1课时）的教学为例进行探索，谈谈自己在平时的教学过程中，以指向核心素养为目标，设置问题情境的一些做法与体会.

二、问题的设计——问题情境策略举隅

1.趣味性问题情境策略——指向学生经验，经历思维抽象过程

章建跃教授在《数学教育心理学》一书中指出，学生获得概念的能力，随年龄、经验、智力而发展，研究表明，三者中经验的作用更大，丰富的经验背景是理解概念本质的前提.因此，我们引导学生从自己的日常生活中积累有利于概念学习的经验，并激活这些经验，让学生进行分析、比较，发现旧知的局限性，探索新知的合理性，直接指向数学抽象思维.

教学片断1.

师：同学们，你们玩过套圈游戏吗？套圈游戏就是把一个圆圈套到玩具上.如果几位同学按如图1所示的位置站列，你认为游戏公平吗？

生1：不公平，因为他们距离玩具的远近不同，有的远，有的近.

师：那怎么站才公平？

生2：站成一个圆圈.

师：这个圆该怎么画呢？

生3：以玩具为中心，用一根绳子的一头套在玩具上，拉直绳子，另一头旋转一周，就能得到一个圆.

师：根据刚才的画法，如果我们把拉直的绳子看成线段OP，在同一平面内，线段OP绕它固定的一个端点O旋转一周，则另一端点P所经过的封闭曲线叫做圆.固定的端点O叫做圆心，线段OP的长叫做半径，通常用r表示，以O为圆心的圆记作“⊙O”，读作“圆O”.

师：以点A为圆心画圆，可以画几个圆？以3 cm为半径画圆，可以画几个圆？

通过学生动手操作画图，得出等圆和同心圆的概念，并进一步明确了圆心和半径是圆的两个要素：圆心确定圆的位置，半径确定圆的大小.

【设计意图】兴趣是最好的老师.以游戏为载体引入新课，能充分调动学生的知识储备和学习积极性.从教育心理学角度来看，概念是思维的基本单位，概念增加了经验的意义.看到“圆”这个词，学生的大脑中从一般的圆的表象抽象出平面图形、封闭的、圆心到圆上各点的距离相等（定义）等.学生对概念的理解就从具体水平向抽象水平发展，从日常概念向科学概念发展.

2.探究性问题情境策略——指向数学直观判断，获得“精致”过程

史宁中教授认为，数学知识的形成依赖于直观，数学知识的确定依赖于推理.也就是说，在大多数情况下，数学的结果是“看”出来的，而不是“证”出来的，所谓“看”，是一种直觉判断，这种直觉判断建立在长期有效的观察和思考的基础上.在教学中，我们要精心设置探究性问题，引导学生观察和思考，使其在丰富的教学活动中积累直观判断的经验，“悟”出门道.

教学片断2.

师：除了圆心、半径，你还学过哪些有关圆的概念？

生4：圆的直径、周长、面积.

师：很好，除此之外，这节课我们将对圆有一个新的认识.如图2，在圆上任取两点A，B，这两点将圆分成了两部分，我们把圆上任意两点间的部分叫做圆弧.图2中的两条弧有什么不同？

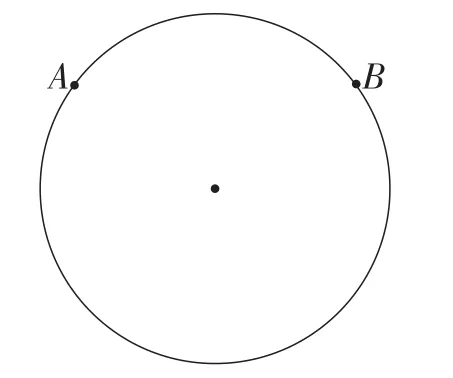
图2

生5：一条弧长，一条弧短.

师：如果点A固定不动，沿圆周移动点B，在点B移动的过程中，两条弧会不会相等呢？点B移动到什么位置时两条弧相等？

生6：当点B运动到点C，即AC恰好是圆的直径时（如图3），这两条弧相等.

图3

师：两条弧相等时，这两条弧都叫做半圆.我们把比半圆小的弧叫做劣弧，比半圆大的弧叫做优弧.那么，是如何知道这两条弧（半圆）相等的呢？

生7：圆是轴对称图形，沿直径AC折叠，直径两旁的部分能完全重合.

师：在同圆和等圆中，我们把能够完全重合的弧叫做等弧.

师：如图4，连接AB两点得到一条线段，我们把连接圆上任意两点的线段叫做“弦”.当点A固定不动，点B沿圆周移动的过程中，观察弦AB的长度，大家有什么发现？

图4

生：当AB为直径时，弦AB最长.

师：通过刚才的操作，大家能说说直径和弦的关系吗？

生：直径是最长的弦，但弦不一定是直径.

【设计意图】学生在学习某个概念时，可能会利用自身的生活经验对所学概念进行拓展延伸，有时甚至会做出某种推论，这个过程被心理学家称为“精致”，精致的实质是对数学概念的内涵与外延进行详细的加工.与圆有关的概念很多，教师要在课堂上充分挖掘其内在的必然联系，从弧入手，通过连接得到弦，并以此为主线，将看似杂乱无章的概念有机地串联起来，将运动观念、极限思想和特殊与一般的转化融入其中，使静态的内容变得灵活生动.

3.思辨性问题情境策略——指向理性思维，对话概括和表达能力

理性思维是在数学学习过程中，通过观察、体验、经历及内化等过程逐步形成理性的思考问题、分析问题、解决问题的思维方法和价值观，是数学核心素养的灵魂所在.在初中数学教学中，根据教学内容设置合理的思辨性问题，有助于学生明晰知识内涵，完善认知结构，促进数学理性思维的有效形成.

教学片断3.

师：为什么站在圆上进行套圈游戏就公平了呢？

生8：因为他们到圆心的距离都相等，都等于半径.

师：如果点到圆心的距离为d，圆的半径为r，当点在圆上时，d=r.

问题1：如图5，同学甲站在图中点A处，同学乙、丙两人也想来参加比赛，他们分别站在图中的点P，Q处，如果你是甲同学，你会有什么看法？

图5

学生经过思考得出这样游戏不公平，丙更占优势，因为乙到圆心的距离大于半径，丙到圆心的距离小于半径，即点在圆外→d＞r，点在圆内→d＜r.

问题2：后来学生丁也来参加游戏，他站在图中的点M处，但是地上的线已经模糊了，问同学丁怎样才能知道自己恰好站在圆上呢？

学生小组交流后得出当点M到圆心的距离等于半径时，同学丁恰好站在圆上，即d=r→点在圆上，另外，d＞r→点在圆外，d＜r→点在圆内.

师：好，也就是说由点与圆的位置关系能得到d与r的数量关系.反过来，又可以由d与r的数量关系来刻画点与圆的位置关系.

【设计意图】紧扣情境引入主题，适时进行追问，引导学生总结、归纳出用点到圆心的距离与半径之间的数量关系来刻画点和圆的位置关系.通过游戏的方式设置问题情境，既符合知识的逻辑顺序和学生的认知规律，也使得学生在轻松愉悦的环境中加深了对知识的理解，教学环节更加自然顺畅，水到渠成.

4.实际性问题情境策略——指向数学模型的建立，深加工应用与拓展

数学建模是指对现实生活问题、科学问题或数学问题建立数学模型.数学建模是一种数学的思考方法，是运用数学的语言和方法，通过抽象、简化建立能近似刻画并解决实际问题的强有力的数学手段，不仅可以帮助学生发现解决问题的途径，而且能够优化问题的解决过程，为数学知识的发现与形成提供有效的思路.

教学片断4.

问题3：如图6，在A地正北80 m的B处有一幢民房，正西100 m的C处有一变电设施，在BC的中点D处是一古建筑.因施工需要，必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏，问爆破影响面的半径应控制在什么范围内？

图6

问题4：BC是一条街道，为了保障街上行人的安全，问爆破影响面的半径应该控制在什么范围内？

【设计意图】以实际问题为载体，初步构建数学模型，引导学生利用点到圆心的距离d与半径r的大小比较，来判断点与圆的位置关系.培养学生用数学的眼光观察世界，用数学的语言表达世界，增强学生的数学应用意识，从而促进学生数学抽象、数学建模能力的发展.

5.螺旋式问题情境策略——指向数学逻辑推理，感悟隐性的思想方法

《标准》指出，推理能力的发展应贯穿在整个数学学习过程中.推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式.推理一般包括合情推理和演绎推理.虽然数学学习并不是纯粹的逻辑过程，但是逻辑推理是公认的数学核心素养之一.章建跃教授曾说，推理是数学的命根子.通过多角度的螺旋式问题探究，可以加深学生对知识内涵的了解，进而帮助其巩固所学知识.

教学片断5.

问题5：如图7，四边形ABCD为矩形，对角线AC，BD交于点O.则A，B，C，D四点在以点O为圆心的同一个圆上吗？

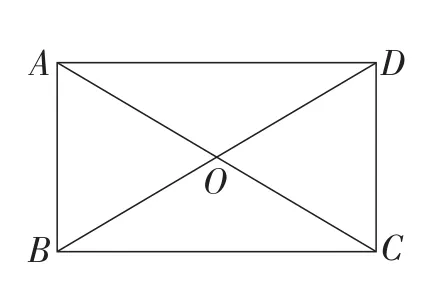
图7

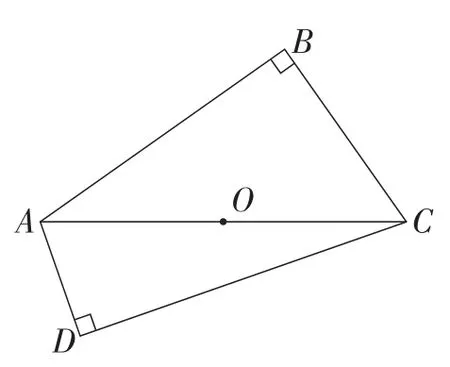
图8

问题6：如图8，在四边形ABCD中，∠B=∠D=90°，O为AC的中点.则A，B，C，D四点在以点O为圆心的同一个圆上吗？

问题7：如图9，让同学站列在三角形的三个顶点处进行抢凳子游戏，凳子放在何处游戏公平？

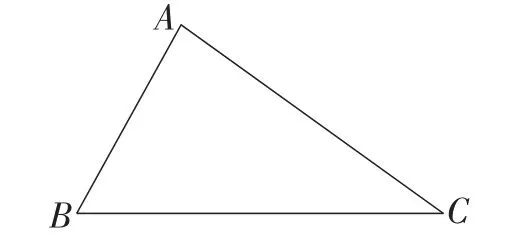
图9

【设计意图】通过层层递进的问题串，由浅入深，螺旋上升，帮助学生进一步巩固了所学的知识，同时也将本节课的知识进一步升华.通过多途径、多角度螺旋上升的问题，深入挖掘题目之间的本质内涵和联系，有助于学生实现自我突破和逻辑推理素养的发展.

三、问题的解决——基于课例的几点思考

课堂教学是核心素养落地的重要阵地.问题情境作为课堂教学的重要支点，它承担了激发学生学习兴趣、引发认知冲突、开放启迪思维等重要作用.现代理念的教学倡导这样的模式：问题情境—建立模型—解决模型—回归问题—调整优化—应用拓展.从中不难看出，问题情境是教学的必要环节，是课堂教学的驱动力所在.在数学教学中创设有效的问题情境，笔者认为有如下一些基本策略.

1.构建生活化的问题情境，为培养学生的核心素养接力

数学学习离不开生活.构建生活化的问题情境就是从学生的生活经验和已有的知识出发，构建与学生生活紧密联系的、符合知识需要的问题情境，使学生置身于实际生活中去发现问题，然后用数学的眼光观察生活，用数学的思维思考现实问题，进而用数学的方法解决问题.让学生在发现问题、分析问题、解决问题的过程中，增强“用数学”的意识，提高“用数学”的能力，体验“用数学”的乐趣，从而发展核心素养.

2.创建多元化的问题情境，为培养学生的核心素养发力

陈鹤琴先生在他倡导的“活教育”理念中提出“大自然、大社会都是活教材”.因此，为了激发学生的积极参与，唤醒学生思考的内在动力，除了把数学问题生活化以外，我们还可以借助其他手段，激发学生的求知欲，促使学生愿学、乐学，实现最佳的学习效果.例如，我们熟悉的变式教学，就是在统一的问题情境下，多角度改变学生的认知条件，让学生多层次理解问题的本质，达到举一反三、触类旁通的效果.

3.搭建阶梯性的问题情境，为培养学生的核心素养添力

阶梯性的问题设置就是把某个较为复杂的问题分解为若干个相互独立，但又循序渐进、难度逐渐增加的问题串，通过设置一系列有针对性的问题串，启发学生思维、突破教学难点，进而促进学生不断达成探究目标的一种有效方法.在问题串的设计过程中，根据学生已有的生活经验和知识水平，创设彼此关联、由易到难、富有层次性的问题情境，激活学生的思维，培养其科学探究的能力.

4.营造开放性的问题情境，为培养学生的核心素养助力

开放式问题是一种探索性的问题，探索性问题的设置能够引导学生依托所学知识多角度去思考与解答问题.数学探究和数学建模是新课程中的一大亮点，尤其是各种数学探究活动，在整个教学体系中，贯穿于教学活动的始终.教师在教学中通过对开放式问题情境的创设，引导学生主动去探究不同的策略，努力去求解目标问题，促进学生打开思路，提高自身的探究能力与创造能力，深化数学思维.

总之，数学教学要掌握学生的思维之道、心理之门，善于选择合适的问题情境创设策略，创设基于核心素养、形式多样、内涵丰富的问题情境，培养学生的问题意识，让学生不断经历情境、问题及问题解决的过程，提高学生的综合能力，使核心素养的培养落到实处.