挖掘真题价值 引领教学方向——以2017年北京市中考一道几何综合题为例谈几何教学

（清华大学附属中学朝阳学校）

中考试题是命题专家智慧的结晶，具有典型性和示范性，如何最大化的发挥中考试题在教学中的功效，值得一线教师深入思考和研究.近几年，北京市中考的几何综合题基本都以正方形为背景.实际上四边形的研究过程就是平面几何研究过程的微缩，是对平面几何研究方法的全面展示.笔者以2017年北京市中考试卷第28题第（2）小题为例，谈谈平面几何研究方法，引发几何问题的教学思考，并给出一些教学建议.

题目如图1，在等腰直角三角形ABC中，∠ACB=90°，P是线段BC上一动点（与点B，C不重合），连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M.

（1）若∠PAC=α，求∠AMQ的大小（用含α的式子表示）；

（2）用等式表示线段MB与PQ之间的数量关系，并证明.

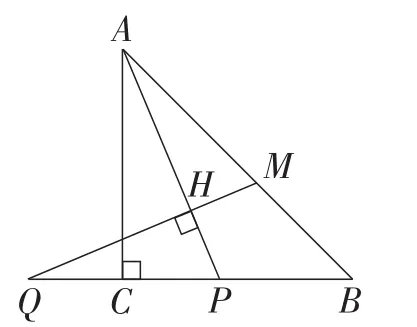
图1

一、试题解析

此题是一道以基本图形为载体的探究题，主要考查轴对称变换、等腰直角三角形等有关知识，考查运用图形变换分析图形中基本量之间的数量关系的探究过程，考查几何直观、推理能力、分析和创造性解决问题的能力.通过调查北京市某区约14 000名学生的得分情况，可知：此题第（2）小题的平均分为1.09分（满分为5分），得分率只有22%.

笔者针对所授课班级35名学生进行了全面调查，给每名学生20分钟进行独立思考去做这道题.在实际操作过程中，很多学生很难猜出PQ和BM是倍的关系.猜出来是倍关系的学生也很难找到有效的作辅助线的方法，即使通过种种方法构造出了全等三角形，找到PQ和BM的联系，学生却被困在了如何证明AQ=QM上，这也是导致很多学生伪证的原因.通过调查学生的实际情况，学生提出如下困惑：有的提到文字叙述烦杂，不知如何利用好已知条件；还有的提到图形复杂，图形的边角关系混乱让人无从下手.

在对这些学生的调查过程中，发现存在如下需要解决的问题.

问题1：会猜想PQ和BM的数量关系；

问题2：想到连接AQ，以及利用AP=AQ得到其他可用的结论；

问题3：能联想到第（1）小题中∠AMQ=45°+α对第（2）小题的作用；

问题4：通过有效的手段找到线段PQ和线段BM之间的联系.

上述调查结果反映出：一方面，大部分学生通过两年半的学习，已经初步掌握了解决几何综合问题的知识储备；另一方面，虽然学生基础较好，但是由于几何综合题具有信息量大、字母符号多、图形复杂等特点，学生的推理能力还比较薄弱，面对探索性、存在性等问法，缺少明确的解题目标，难以找到解题方向.此外，由于时间紧、任务重，这就需要教师在中考复习阶段，最大限度地挖掘历年中考试题的价值，借“题”发挥，借“力”拓展，灵活进行变式训练，激发学生的好奇心和求知欲，促使学生的思维向多方向、深层次发散.因而教师如何引导学生获得解决几何证明题的一般思路，甚至在变化的过程中通过动中求静找到不变量的解题策略，从而解决一类题，就变得尤为重要了.

二、解题策略研究

1.合理猜想

为了让不同层次的学生都有收获，猜想MB与PQ两条线段的数量关系无非是通过度量，或通过找特殊位置将动态化静态，大胆假设，精心求证，从而发展学生的合情推理能力.

方式1：度量猜想.通过测量MB与PC的长度猜想结论；

方式2：特殊角度验证.如图2，过点M作MN⊥QB，交QB于点N.若 ∠Q=∠PAC=30°，设PC=QC=1，则在△BQM中，由∠Q=30°，∠B=45°，设MN=x，则可得解得x=1.因此MB=2.所以

图2

【点评】上述方法从特殊到一般发展学生的合情推理能力，也解决了上述问题1.此外，如图3，当点P与点B重合时，在这种特殊端点情况下，也能得到实际上根据经验可知，出现等腰直角三角形一般会有倍的数量关系，出现等边三角形或者含30°角的直角三角形，则一般会有倍的数量关系.

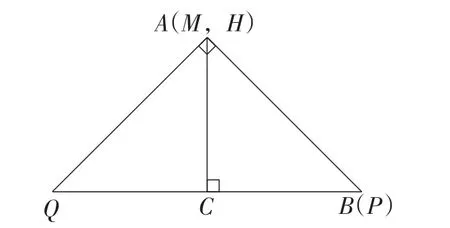
图3

2.审图形或结论明确解题目标

从图形出发思考问题，由图1可直观联想到正方形中的基本图形.如图4，在正方形QNEF中，若QM⊥AP，可证明出△ACP≌△QNM.从这个基本图形出发，可自然而然地想到原题目的辅助线作法.原题目中，可以过点M作MN⊥BQ于点N，将问题转化成证明△ACP≌△QNM.或者从结论出发思考问题，通过合理猜想获得后明确解题目标，通过过点M作MN⊥BQ于点N，从而将结论转化为MN=PC，进而去证明△ACP≌△QNM.

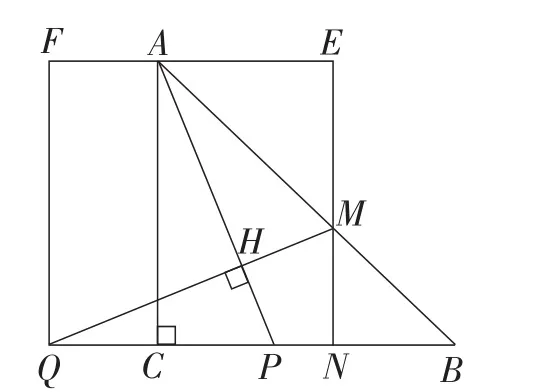
图4

【点评】借助图形直观，先把研究对象抽象为基本图形，再把对象之间的关系转化为图形之间的关系，使问题变得简明，从而解决了上述问题4.在几何直观结合边角关系的引导下，可分别以△ACP和△QNM为目标构造全等三角形，进而解决问题.

3.审条件获得轴对称下的边角关系

结合此题条件，已知CQ⊥AC，CQ=CP，指向线段QP的垂直平分线为AC.由垂直平分线的性质，想到连接AQ.事实上，由于AC垂直平分PQ，可知点P和点Q关于直线AC是成轴对称的，那么△QAC≌△PAC.进而得对应角 ∠APQ=∠AQP，∠PAC=∠QAC=α. 得到轴对称的相关边角关系，即AQ=AP.

【点评】事实上，由于AC垂直平分PQ，可得点P和点Q关于直线AC是互为对称点的，这就解决了上述问题2.如果仅仅体现垂直平分线而不上升到轴对称，学生很难联想到连接AQ，并得到一系列的边角关系.

4.联系第（1）小题的结论

如图5，连接AQ后得到轴对称图形的相关边角关系，即∠CAQ=∠PAC=α.因此∠MAQ=45°+α.在第（1）小题中，有∠BAP=45°-α，从而在Rt△HAM中求出∠AMQ=90°-∠BAP=α+45°. 联系第（1）小题的结论，可知∠AMQ=α+45°=∠MAQ.综合角的关系，得出AQ=QM.因此MQ=AP.由此可得△ACP≌△QNM.

图5

【点评】审清题意、找到解题的入口是解题的前提.全面审题要做好“三审”，即审条件，审结论，审图形，并注意隐含条件.要对照图形找到它们之间的关系（若题目没有给出图形，要边读题边画出图形），通过审结论明确解题目标.但是，由于条件和结论距离甚远，很可能找不到解题的方向，那么，就要对条件逐一进行转化，向着结论指示的解题目标转化，同时也转化结论，一旦对接，就找到了问题解决的突破口.此外，前一问的解题策略可以启发或影响后一问的思路获得.当学生挑战到最后一问时，如果解题思路遇到困难，则需要退回上一问，将上一问的问题结构看清，成果扩大，这样就能获取更多的思路.

三、教学建议

1.重视基本图形分析，提升直观想象能力

史宁中教授在《数学思想概论》中说到，直观是一种判断能力，是凭借直觉对事物做出直接判断的能力，包括从条件预测结果的能力，也包括由结果探究成因的能力，这种能力依赖于专业知识，更依赖于经验的积累，依赖于经验的浓缩，依赖于经验的升华.

教师要在不断持续的教学过程中，引导学生积累活动经验，直观感受基本图形，形成解决几何综合题的直观能力.要让学生掌握一些重要的基本图形，除了三角形、平行四边形、圆等，还有数轴、网格纸、直角坐标系等.在教学中要有意识地强化学生对基本图形的运用，引导学生运用基本图形去发现、描述问题，理解、记忆结果，这应该成为教学中关注的目标.

如图6，重新认识此题图形时，可以在头脑中让图形动起来，看成是三角形通过平移得到的图形.在几何直观的背景下，运用图形变化去研究图形各要素之间的位置关系与数量关系.

图6

2.多维数据提取，合理实施猜想，科学验证猜想，培养学生的推理能力

从几何直观到逻辑推理可以培养逻辑思维的严密性，体验思维的形成过程.我们在教学中应该着重培养学生用正确的思维方法思考问题，让学生合理地、合乎逻辑地思考问题，在过程中感悟数学基本思想，积累数学活动经验，从而培养学生的逻辑推理能力.

如图3，在探索线段PQ与BM数量关系的过程中，引导学生通过合情推理发现结论通过等腰直角三角形MNB把结论转化为证明MN=PC后，可借助图形直观进一步将结论转化为证明△ACP≌△QNM.在这个过程中明确解题目标，并培养学生从结论到需知的思维过程.

在证明全等的过程中，由已知CQ⊥AC，CQ=CP，可连接辅助线AQ得到轴对称图形的相关边角关系，即∠APQ=∠AQP，∠PAC=∠QAC=α，AQ=AP，进而可联系第（1）小题的结论得到△AQM是等腰三角形，从而得到证明三角形全等的关键条件，即AP=MQ.在这个过程中注重培养学生从图形形成开始，从已知到可知的思维过程.

从已知到可知，从结论到需知，脚踏实地的在每一个地方都给学生提供思维训练的机会，让学生能够熟练地发现或推导图形中各元素之间的关系.究其原因是教会学生这样思考问题才能反映初中几何学习的本质问题，这是解决几何综合题的一般方法.

3.通过一题多解、一题多变，发展学生的创新思维能力

探寻一道题的多种解法，可以拓宽学生的解题思路，形成基本的解题方法，使学生对数学问题进行多角度、多方法、多层次的讨论和思考，自然得出每种解法，能帮助学生突破推理证明的难点.此题第（2）小题可以有如下解法.

解法1：从全等的角度.如图7，延长AC至点D，使得PC=CD，构造△APD，证明△APD≌△QMB.

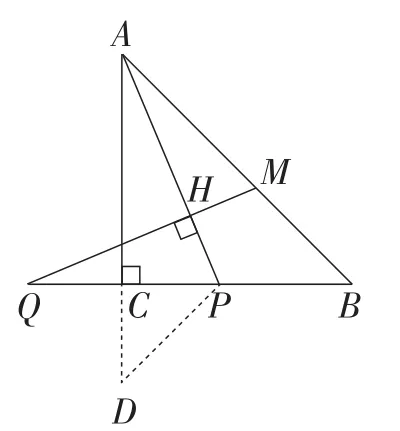
图7

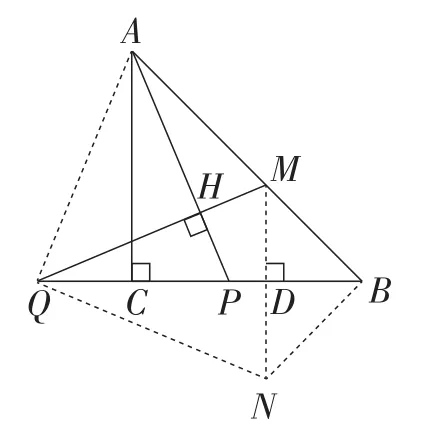
图8

解法2：从全等的角度.如图8，连接AQ，作点M关于BQ的对称点N，连接QN，BN，证明△QAP≌△NQM.

解法3：从计算的角度.如图9，连接AQ，过点M作MD⊥BQ，垂足为点D，设AP=QM=AQ=x，则PC=QC=MD=xsinα. 得问题得证.

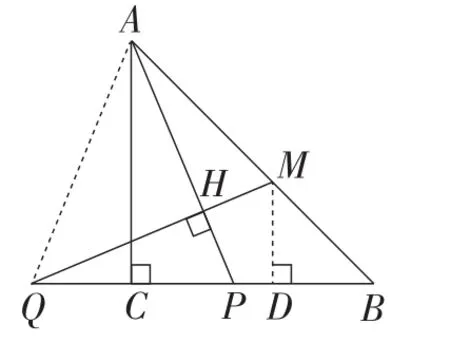
图9

解法4：从图形变换的角度.如图10，平移QM至PE，过点E作EN⊥BP，交QB的延长线于点N，连接BE.由AQ=QM=AP可证明全等，故AC=PN=BC.因此PC=BN=EN.△BEM为等腰直角三角形.问题得证.

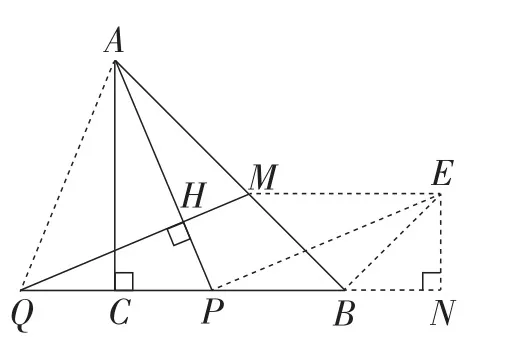
图10

解法5：从图形变换的角度.如图11，过点P作PD∥MB，交AC于点D，只要能证明DP=MB，就能达到平移的效果.取ME=MQ，交QB的延长线于点E，可证得△MBE≌△PDA.问题得证.

图11

充分地利用变换去认识、理解几何图形是培养学生的几何直观的好方法.从图形变化的角度看待图形，借助平移、轴对称图形变换感受直观，可以培养理性思维，获得解决此类问题的思路.鼓励学生运用多种不同方法进行解题，加强学生对于知识和方法的理解和变通，最大限度地挖掘中考试题的价值，从而可以达到培养学生良好思维方式和创新意识的目的.

教师可将题目精讲精练，并进行一题多变，引导学生进行更深层次的思考，经历动态变化过程，发现更一般的结论，通过对已知条件的分析，构造基本图形，感受图形运动变化中的不变量，进而发现解题思路.通过实施不同形式的多种变化，加强学生对于知识和方法的理解和变通.例如，2017年北京市中考试卷第28题可以进行如下变式.

变式1：在等腰直角三角形ABC中，∠ACB=90°，P是线段BC的延长线上的任意一点（与点B，C不重合），连接AP，Q是线段BC上一点，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M.用等式表示线段MB与PQ之间的数量关系，并证明.

变式2：在等腰直角三角形ABC中，∠ACB=90°，点P是线段CB的延长线上的任意一点（与点B，C不重合），连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M.用等式表示线段MB与PQ之间的数量关系，并证明.

以上两道变式题可以让学生根据题意自主画出图形（如图12、图13，其中虚线为辅助线），既培养学生的作图能力，又让学生在操作中直观领会运动的过程和图形的变化规律.

图12

图13

从一道题目的多种解法出发到不断改变题目的条件，进一步挖掘习题中蕴含的思维价值，达到深化价值引领、凸显数学思考的目的.在操作中直观领会运动的过程和图形变化规律.

在平时教学中，教师可以适当加强对典型中考试题的挖掘，精心设计教学问题，构建有价值的探索活动，通过拓展、探究，把问题分析透彻，展示数学知识发生、发展和应用的过程，有意识、有目的地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，帮助学生形成对几何研究方法的整体认识.