多角度思维，妙求离心率*——一道重庆高考模拟题的多解剖析

☉重庆市荣昌中学校 李海堂

在高中数学中，圆锥曲线离心率的求解一直是热点问题，也是近年来高考、竞赛、自主招生考试中比较常见的一类问题，处理这类问题的关键就是准确构建关于基本量a、b、c之间的等量关系.下面结合2019年重庆市高三一模第11题对有关双曲线求离心率问题加以剖析，通过多角度思维的切入，来巧妙地求解离心率.

题目（2019年重庆市高三一模第11题）已知双曲线（ ， ）的左右焦点分别为 、，双曲=1a＞0b＞0F1F2线C与圆x2+y2=a2+b2在第一象限的交点为P，∠PF1F2的角平分线与PF2交于点Q，若4|PQ|=3|F2Q|，则双曲线C的离心率为（ ）.

分析：本题把双曲线与圆的交点、角平分线及线段长度的关系、角度关系等问题加以交汇，结合了圆锥曲线与解析几何初步的相关知识，同时把三角函数的相关知识融合进来，有效地进行了知识的整合，如何巧妙地利用题目中的关系是解决问题的关键.根据本题条件，利用勾股定理、三角函数、直线与方程、平面向量、平面几何性质等不同知识模块中的方法来处理，通过从不同角度的思维来切入，可以收到不错的解题效果.

思维角度1：设∠QF1F2=θ，PF2=x，结合题目中的关系有∠PF1Q=θ，∠PF1F2=2θ，通过题目条件建立有关三角函数的等式，并求得tanθ的值，在直角三角形PF1Q中求出|PF1|和|PF2|与a的等量关系，再在直角三角形PF1F2中找出a与c的等量关系，从而求得离心率.

解法1：如图1所示，设∠QF1F2=θ，|PF2|=x，|F1F2|=2c，则∠PF1Q=θ，∠PF1F2=2θ. 因为在直角三角形PF1F2中，，

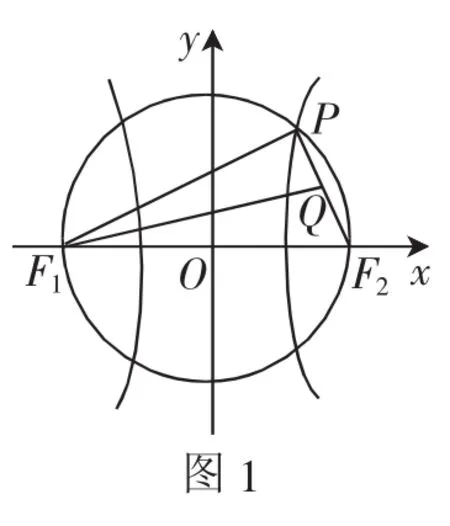
又在直角三角形PF1Q中，

又4|PQ|=3|F2Q|，Q在线段PF2上，所以.

又由双曲线的定义知|PF1|-|PF2|=2a，所以|PF1|=x+2a.

在直角三角形PF1Q中，tanθ以x=（7+3）a.

在直角三角形PF1F2中，，即（x+2a）2+x2=4c2，

所以答案选A.

思维角度2：由已知条件联立双曲线与圆的方程求出点P的坐标，根据题目条件可得→ → ，0），由向量的坐标运算求出Q点的坐标，又Q点在直线F1Q上，且直线FQ的方程为（x+c），进而得到a与c的1等量关系，从而求得离心率.

又b2=c2-a2，

故答案选A.

思维角度3：连结OP，由解法1知tan，根据题目中的已知条件可知|OF1|=|OP|，则∠POF2=4θ，从而可以计算出tan∠POF2的值，进而求得sin∠POF2、cos∠POF2的值，故可得P点的坐标为（ccos∠POF2，csin把P点的坐标代入双曲线方程，进而建立等式并得到a与c的等量关系，从而求得离心率.

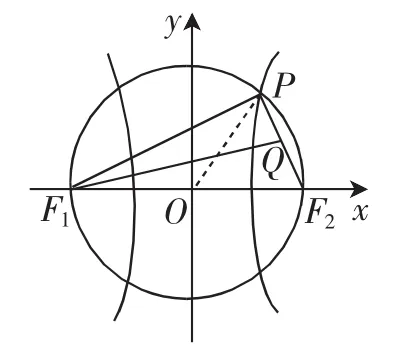
图2

解法3：如图2所示，连接OP，由解法1知tan，则

则c2＞64a2，所以e2＞64.故e2=64+24，即e=6+2.故答案选A.

思维角度4：连结OP，根据解法3求得P点的横坐标为c，又由解法2知P点的横坐标为，进而建立等式并得到a与c的等量关系，从而求得离心率.

解法4：由解法3可知P点的横坐标为，又由解法2可知P点的横坐标为

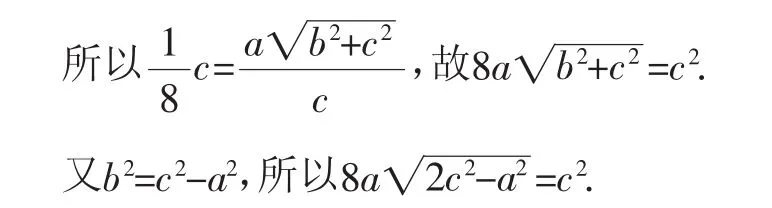
两边同时平方整理可得c4-128c2a2+64a4=0，

以下步骤同解法3.

思维角度5：连结OP，根据解法3可求得P点的纵坐标为，又由解法2可知P点的纵坐标为，进而建立等式并得到a与c的等量关系，从而求得离心率.

看似一道简单的双曲线离心率求值问题，选择方法不同，运算的难易程度就有较大的区别.通过认真分析，仔细研究，选择合适的方法和途径，从多个不同思维角度来切入，巧妙地把该题的底蕴充分挖掘出来，真正体现了对知识的融会贯通.通过一题多解，开拓学生的解题视野，有效地促进学生思维品质和创新能力的提升，从而提升学生的数学思想方法和核心素养.W