用“数学期望”来决策

☉江苏省启东中学 龚凯宏

离散型随机变量的数学期望是概率的自然延伸，离散型随机变量的“决策”类应用题，以其贴近实际生活的题目为背景，成为近年来高考的热点，这类试题的综合性强，应用性广，情景新颖，有力地考查了学生在新情境下分析问题和解决问题的能力.本文撷取几例，谈谈如何解决这类问题.

一、随机变量的数学期望与固定值比较

例1（江苏省启东中学2017高三模拟题）吕四渔港某渔船对下周是否出海作出决策，若出海后是好天气，可通过正常捕鱼获得收益8000元，若出海后天气不好，将因徒劳往返而损失2000元，若不出海不论天气好坏都要承担500元的损失费，据预测下周是好天气的概率为0.4，坏天气的概率为0.6，问该渔船应如何作出决策（即选择是否出海）？

分析：是否出海的决策，其主要依据是经济效益的高低，由题意知：不出海的收益是-500元，是确定的；而出海的收益取决于天气的好坏，只要求得出海的收益的数学期望（即均值）并作出比较，便能作出决策.

解：设X是出海的收益数，由题意可得概率分布为

可求得出海的收益的数学期望值为：

E（X）=8000×0.4＋（-2000）×0.6=2000（元）；

因为E（X）=2000元显然高于不出海的收益-500元，

故该渔船下周应选择出海.

评注：本题是一道基础题，主要考查学生对离散型随机变量的数学期望的实际应用能力，题目背景新颖.天气的好坏是一个不确定因素，合理的决策取决于最好的收益，利用求出收益的数学期望来解决实际问题.

二、两组随机变量的数学期望间比较

例2（2018南通市高三数学学科基地测试）某手机大卖场进行促销活动，促销方案是：顾客每消费1000元便可获得奖券一张，每张奖券的中奖概率为，中奖后商场返还顾客现金1000元.小李购买一台价格2400元的手机，只能得到2张奖券，于是小李与同事小王商量决定补偿50元给同事小王，让小王买了一台价格600元的天翼手机，这样小李可以得到3张奖券，同行的小张认为小李这样不划算.请问小李这样出资50元多得到一张奖券，到底是否划算？请说明理由.

分析：解决本题的关键是：小李若出资50元则得3张奖券，若不出资50元则得2张奖券，对小李实际出钱数这两组随机变量的数学期望进行比较.

解：设小李出资50元抽奖后的实际支出为X（元）；不出资50元抽奖后的实际支出为Y元.

那么X的可能取值为：-550，450，1450，2450；Y的可能取值为：400，1400，2400.

这样X的分布列为：

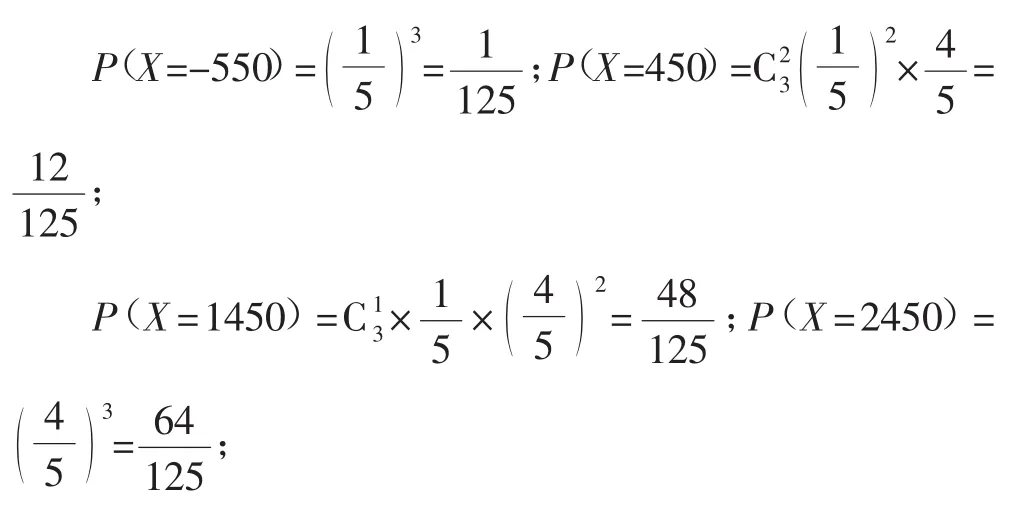
则小李出资50元抽奖后实际支出的数学期望为E（X），

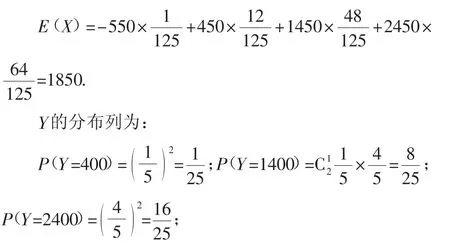
则小李不出资50元抽奖后实际支出的数学期望为E（Y），

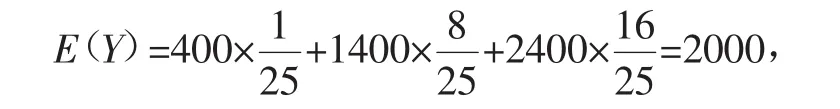
显然E（X）＜E（Y），

因此，小李出资50元增加一张奖券是划算的.

评注：本题是对两组随机变量的数学期望进行比较，从而选优的一类实际应用题，这类题在各类考试中比较常见.正确分辨两组随机变量，并计算出它们的概率分布是解决这类问题的前提.

例3在某学校组织的一次篮球投篮比赛中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分，如果前两次得分之和超过3分即停止投篮，否则投第3次，然后计算得分作为比赛成绩.已知某同学在平时的训练中在A处的命中率q1为0.25，在B处的命中率为q2，且该同学先在A处投一球，以后都在B处投，用X表示该同学投篮训练的总分，其中P（X＝0）＝0.03.现该同学有两种参加方案：甲方案是先在A处投一球，以后都在B处投；乙方案是只在B处投篮.根据平时的训练成绩该同学应选择哪种方案？

分析：解决本题的关键是：先求出该同学在B处的命中率，然后分别求出这两种方案中得分的数学期望，通过比较两种方案各自的数学期望，再从中选择合适的方案.

解：由题设知，“X＝0”对应的事件为“在三次投篮中没有一次投中”，

因为q1＝0.25，所以解得q2＝0.8.

因此甲方案的数学期望E（X）＝0×0.03＋2×0.24＋3×0.01＋4×0.48＋5×0.24＝3.63.

如果用乙方案：

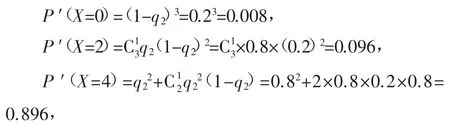
因此乙方案的数学期望E′（X）＝0.008×0＋0.096×2＋0.896×4＝3.776.

因为E′（X）＞E（X），即乙方案的平均得分更高.

所以在比赛中该同学应选择使用乙方案.

评注：本题是关于离散型随机变量的一道综合题，题中的已知条件没有直接给出在B处的命中率，要先求在B处的命中率，才能求出两组随机变量的数学期望，通过对数学期望进行比较，从而解决选优的一类实际应用题.

三、随机变量的数学期望与函数结合

例4（2009南通市第二次调研测试）某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量，它的分布列为1，2，…，12）；设每售出一台电冰箱，电器商获利300元.如销售不出，则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大？

分析：解决每月初购进冰箱的台数，取决于月收益的数学期望，又因为每月收益是随机台数ξ的分段函数，所以本题的关键是列出收益关于随机变量ξ的函数关系式.

解：设x为电器商每月初购进的电冰箱的台数，依题意，只需考虑1≤x≤12的情况.

于是电器商每月获益的均值即数学期望为：

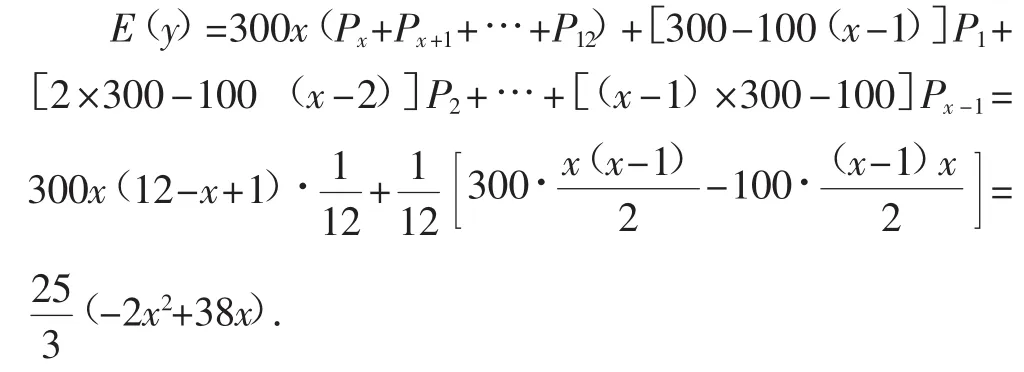
因为x∈N*，所以当x=9或x=10时，数学期望最大.

答：电器商每月初购进9台或10台电冰箱时收益最大，最大收益为1500元.

评注：本题是通过求离散型随机变量均值以解决实际问题，本题的一个“亮点”是巧妙地将概率知识与二次函数融合起来，考查了离散型随机变量的概率、均值、分段函数以及二次函数区间内的最值等知识点，既考查了考生的基础知识又考查了考生的逻辑思维能力.

数学期望是离散型随机变量的一个重要特征，它体现了随机变量的平均水平，是解决“决策”类实际应用题的“衡量标准”.F