提高课堂效率,减轻学生负担
——关于几何体的外接球问题
2019-08-03四川省内江市隆昌市第七中学
☉四川省内江市隆昌市第七中学 易 琴
☉四川省内江市隆昌市第一中学 陈 强
进入高三下学期,留给学生的时间越来越少,精力也越来越有限,对我们老师的要求也越来越高,势必要求我们提高课堂效率,以减轻学生的负担.那么,怎样才能提高课堂效率呢?下面笔者就以“几何体的外接球问题”为例,设计一堂探究课,谈谈笔者自身的一些看法.
一、研究考纲,明确要求,了解学生学情
根据高考的考纲要求,近几年高考对球的要求从理解变为了了解,但不管怎么降低难度,几何体的外接球始终都是高考的难点与热点.对于空间想象能力较弱的学生来说,平时花了不少时间来训练、练习,但到考试的时候还是一头雾水,感觉无从下手.为了解决这个问题,笔者研究了近几年的高考试题和各地的模拟试题,发现近几年高考对几何体的外接球的考查难度降低了不少,而且绝大部分试题可通过化归转换为两类几何模型的外接球问题,从而使问题轻松得到解决.
二、立足学生,引导探究,制定“特有”方法
1.长方体模型——侧棱垂直于底面、对棱相等的四面体
对于一个长、宽、高分别为a、b、c的长方体,通过分析长方体与球的几何图形(图1),得到关系式:,从而得到与外接球半径相关的式子:(2R)2=,其中c为长方体的高h,而为平面ABCD与球O的截面的小圆直径2r,由此可得:外接球半径的关系式(2R)2=h2+(2r)2.所以对任何一个几何体而言,只要具备“侧棱垂直于底面”,都可化归转换为长方体模型,利用此关系式便可求出几何体的外接球半径,从而降低了对学生空间想象能力的要求.
另外,对于对棱相等的四面体也可转换为长方体模型(图2).
若四面体的三组对棱的长度分别为x,y,z,则(2R)2=

图1

图2
看大家听得都比较疲惫,在讲解完模型后,给出了第一个例题:
例1如图3,四边形ABCD是边长为的正方形,点E,F分别为边BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积为______.
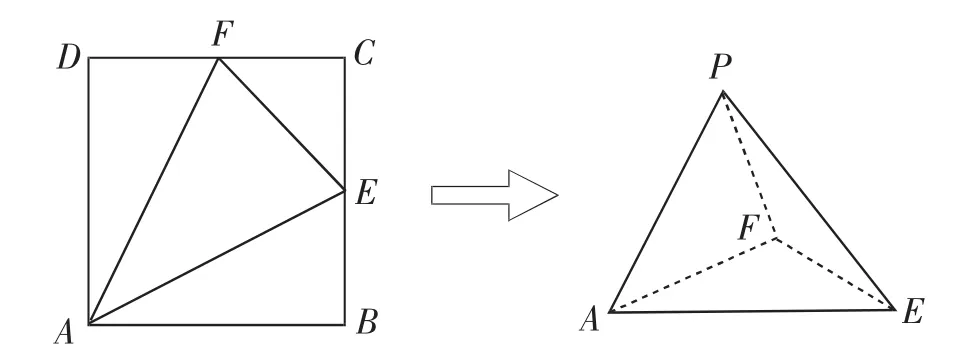
图3
许多空间想象能力弱的学生,看到这个题就感到慌张、烦躁,导致最后直接放弃.于是笔者开始引导学生寻找几何模型,通过分析翻折前后的几何图形,学生很快就发现AP⊥平面PEF,此题具备“侧棱垂直于底面”的特征,可以化归转换为长方体模型.此时,好多学生由刚才的烦躁开始变得活跃,甚至有人说:“只需求得底面PEF所在的小圆的直径即可,而且易得底面小圆直径EF=,AP=2,于是球的半径,所以S表=18π.”
笔者看大家情绪高涨,于是给出了下一个例题(留足5分钟思考):
例2在四面体ABCD中,AD⊥底面ABC,AB=AC=,BC=2,点G为△ABC的重心,若四面体ABCD的外接球的表面积为,则tan∠AGD=______.
刚展示完题目,就有不少学生吼道:“由AD⊥底面ABC可知,此题具备“侧棱垂直于底面”的特征,可化归转化为长方体模型.”也有不少学生开始动笔演算起来;很快有不少学生就给出了标准答案:

图4
所以由公式(2R)2=h2+(2r)2,可得AD=h=4,
于是tan∠AGD=2.故填答案:2.
此时,学生都比较兴奋,于是笔者介绍了第二种几何模型:
2.正n棱锥模型
设正三棱锥S-ABC的高为h,外接球的半径为R,底面小圆的半径为r,由(图5)分析可得OC2=OO12+O1C2,其中OC为外接球半径,OO1为小圆面的圆心与球心之间的距离,O1C为小圆面的半径r,由此可得:正三棱锥外接球半径关系式为R2=r2+|h-R|2,同理对正六棱锥S-ABCDEF而言(如图6),也符合此关系式.
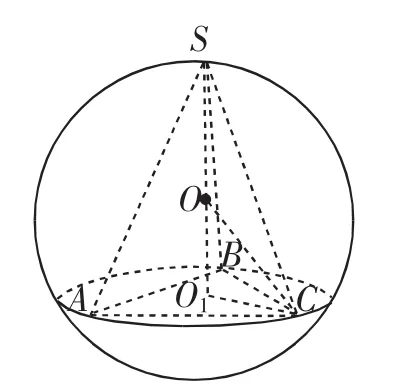
图5
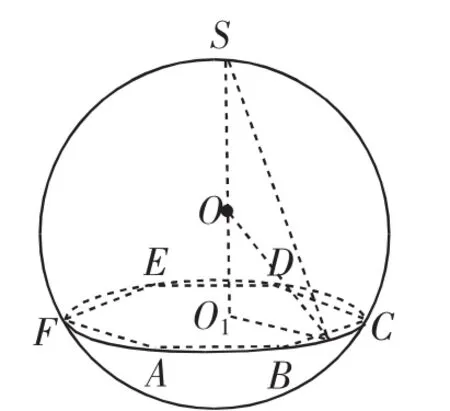
图6
此时,大家都比较期待这个新模型能够发挥作用,于是笔者给出了第三个例题:
例3在边长为2的菱形ABCD中,BD=2,将菱形ABCD沿对角线AC对折,使二面角B-AC-D的余弦值为,则所得三棱锥A-BCD的外接球的表面积为______.
此题不仅考查了关于球的知识,还考查了学生比较薄弱的二面角知识,所以学生刚开始看到此题的时候,有点害怕,不敢做,于是笔者开始引导学生解决二面角的问题:

图7
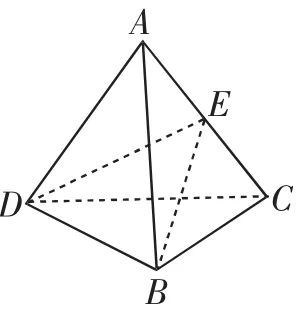
图8
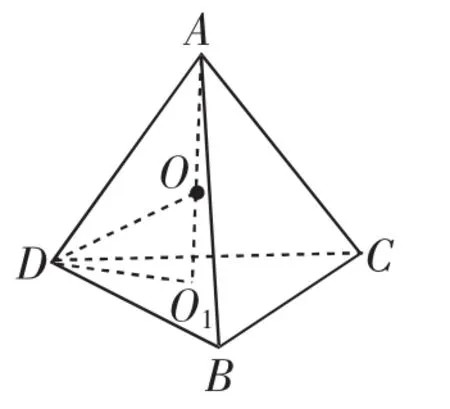
图9
此时,学生已经有了很强的意识——寻找几何模型,很快学生们就给出了下面两种解法:
法1:由于四面体每对棱都为2,所以可将四面体放入棱长为的正方体中,于是球的半径6π.故填答案:6π.
法2:由于正四面体的棱长为2(图9),可得几何体的高,底面小圆的直径由R2=|h-R|2+r2可得解得R==6π.故填答案:6π.
三、学生回味、自我总结、化归本质
至此,本堂课内容全部结束,让学生们自行讨论,并进行自我总结归纳:
学生A:求几何体的外接球都可以用这个方法吗?
学生B:必须具备这两大模型才可以.
学生C:而且这两种模型在计算时,最终都会由几何体的高h、小圆的半径r、外接球的半径R来构成直角三角形,进而利用勾股定理求解.
学生A:若不具备这两种模型,那该怎么求呢?
此时,教室突然安静下来,大家都把疑惑的目光集体投向了老师.
老师微笑着答道:
1.高考对几何体的外接球要求降低,几乎都考这两种模型,此法足以应对高考;
2.解决几何体的外接球、内切球问题,实际上有通法——截面法,这也是我们下次课所要探究的课题.至此,本堂课结束.
一堂有效率的课如何产生呢?笔者认为既要老师认真备课——研究高考考纲、钻研高考真题,又要深入了解学生的难点、弱点——思考具有针对性的解决方案.F
