超短筒谐波齿轮柔轮变厚度杯底的结构最优化设计

2019-07-09邢静忠庞满意

天津工业大学学报 2019年3期

邢静忠，庞满意，张泽

（天津工业大学天津市现代机电装备技术重点实验室，天津 300387）

谐波齿轮传动具有结构简单、体积小、重量轻、传动比大、同时参与啮合的齿对数多，传动平稳、回差小、传动精度高等优点，广泛应用于机器人、航空航天、精密机械和导航指向机构等[1-3]。工业机器人对谐波齿轮传动的传动精度和负载能力提出了更高的要求。在谐波齿轮传动中，柔轮始终承受波发生器引起的装配交变应力，同时负载状态下柔轮筒体还要承受更高的负载应力，易引发柔轮疲劳破坏，故柔轮应力分析是谐波齿轮设计中的基础关键性问题。

针对波发生器作用下柔轮齿圈部位的应力和变形，求解方法主要有理论公式法[4]、实验归纳法[5-6]和数值模拟仿真法[7-10]。伊万诺夫[11]对谐波齿轮传动进行了非常系统的理论研究，建立等效圆环理论计算装配状态下的柔轮变形和应力。通过实验测量负载传动的啮合力，归纳出啮合力分布的经验公式。沈允文等[12]在谐波传动方面也开展了大量基础性理论研究和实验研究。因实验研究耗时且成本高，数值仿真求解应力和变形被越来越多地应用。

刘文芝[13]将Pro/E生成的柔轮和刚轮读入ANSYS模拟柔轮的啮合过程，获得柔轮应力的分布，修正轮齿影响系数。高海波等[9]基于APDL语言建立柔轮参数化接触模型，并讨论筒长、壁厚、齿宽以及倒角半径等参数对柔轮最大等效应力的影响。Li[14]自主开发有限元程序，分别对齿啮式筒形柔轮、变厚度杯底杯形和礼帽形柔轮进行研究，并与实验结果对比。

饶振纲[15]以啮合参数为设计变量，以体积为目标函数对结构尺寸优化设计。Kayabasi[16]提出基于有限元平台的齿廓参数优化方法。Dong等[17]建立谐波齿轮接触模型，并基于动态分析结果，对齿廓参数进行优化；用APDL语言建立柔轮参数化接触模型，以柔轮最小应力为目标，用ANSYS内置的零阶优化方法优化柔轮结构参数[18]。机器人用谐波齿轮要求更小的长径比，如何计算超短筒柔轮应力，并利用变厚度杯底方案的优化设计，提高超短筒柔轮的承载能力成为迫切需要。文献[19]仅从参数敏感性角度指出了对应力降低最敏感的参数，尚未开展最优化设计研究。

本文利用有限元方法研究超短筒柔轮结构参数对柔轮应力的敏感性，以寻找降低应力的结构参数。建立变厚度杯底模型，优化柔轮变厚度杯底，以进一步降低空载装配应力和传动负载应力。首先，建立杯形柔轮实体单元有限元参数化模型，依据标准椭圆波发生器的径向变形规律，在齿圈中面施加径向位移约束，求解空载装配状态的装配应力。依据最大瞬时力矩，在柔轮中面施加啮合力和相应的位移约束条件，获得负载传动状态下的负载应力。分别讨论柔轮长径比、杯底倒圆半径、膜板宽度对装配状态和负载工况下杯底最高应力的参数敏感性，找到应力最低的结构参数。利用三次样条函数构建变厚度杯底，基于APDL语言开发复合形法优化程序对最大装配应力和最高负载应力分别进行杯底厚度优化。最后应用ANSYS内置的零阶和一阶优化程序对装配应力的优化结果进行验证。

1 装配状态和负载应力求解

杯形柔轮是带有轮齿的杯形薄壁壳。工作中往复变化的装配应力和传动应力无法解析求解。利用有限元方法求解柔轮变形和应力是常用的数值分析方法。

1.1 建立柔轮有限元参数化模型

一般将长径比为0.5的柔轮称为短筒柔轮，小于0.5的称为超短筒柔轮。图1为短筒杯形柔轮的结构简图。

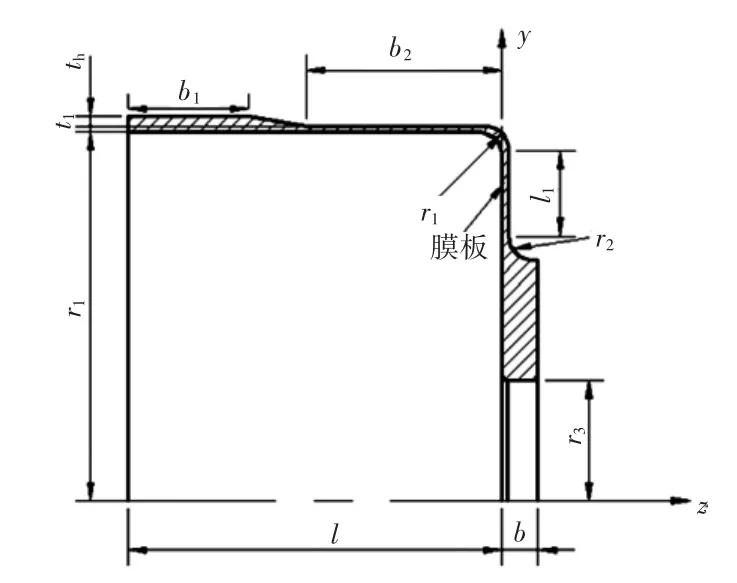
图1 杯形柔轮剖面尺寸Fig.1 Profile dimensions of cup-shaped flexspline

图1中，b1为齿圈宽度。参考HD公司的CSG型25系列，减速比100的杯形谐波齿轮。本文将轮齿抹去只研究杯底应力。根据等刚度要求，由文献[8]求得当量齿圈厚度th=0.81 mm。其他尺寸如表1所示。

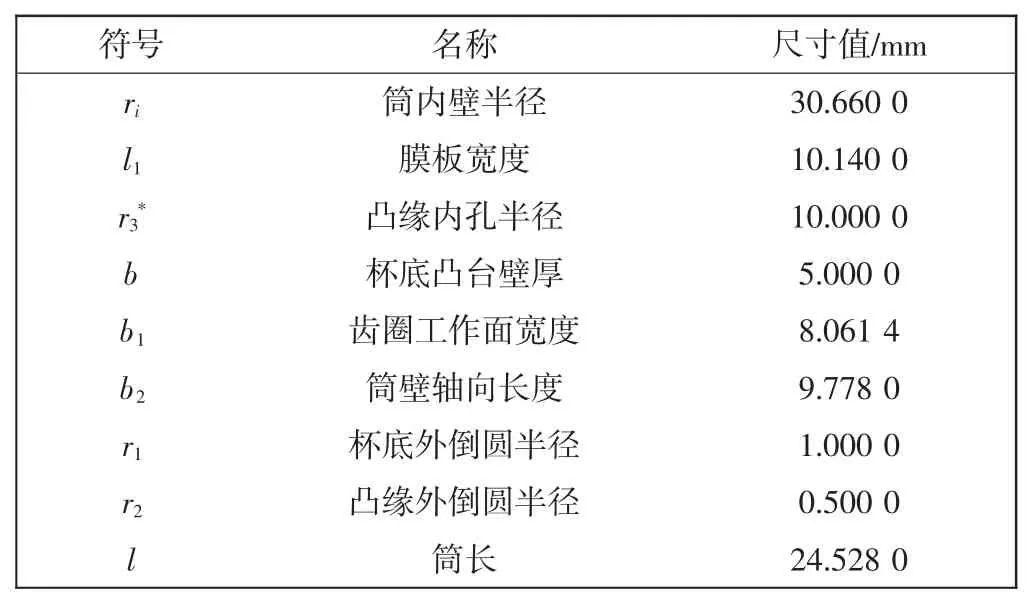
表1 杯形柔轮结构参数尺寸Tab.1 Structural dimensions of flexsp line cup

按表1参数定义柔轮纵向截面上的关键点，依次连接生成四边形面，映射生成四边形平面网格。选用20结点的实体结构单元SOLID95，将平面网格绕回转轴转90°，扫略生成用规则六面体单元的柔轮1/4模型。定义30GrMnSiA合金钢柔轮的弹性模量E=207 GPa，泊松比 μ=0.3。

1.2 标准椭圆波发生器作用下的径向位移约束

受波发生器作用，装配状态下柔轮变形可用中面曲线方程表达。中面曲线是指柔轮壳体中面和垂直于回转轴的柔轮受载平面相交所形成的平面曲线。装配状态下，柔轮变形主要由波发生器的形状决定。常用的波发生器有双圆盘波发生器、四滚轮波发生器、双滚轮波发生器、椭圆波发生器和余弦凸轮波发生器。选用国内普遍应用的标准椭圆波发生器，如图2所示。

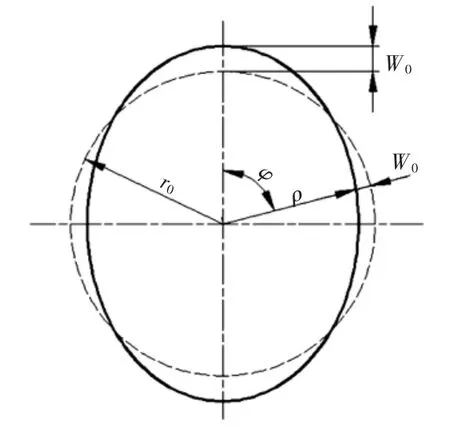
图2 椭圆波发生器示意图Fig.2 Diagram of elliptical wave generator

图2中：r0为变形前柔轮中面半径；W0为最大径向变形量；ρ为任意角度φ处柔轮变形后的径向长度；W为φ处的径向位移。

在标准椭圆波发生器作用下，柔轮的中面曲线

式中：a、b分别为椭圆的长半轴和短半轴，即a=r0+W0，

根据模型在2个纵向截面的对称性，定义对称边界条件约束。按照标准椭圆波发生器的形状，计算出齿圈中面的径向位移，在该位置中面结点处施加径向位移约束，即定义这些结点的径向位移为ρ-r0。考虑到柔轮杯底的安装条件，固定杯底凸缘上的所有结点。

1.3 传动转矩作用下柔轮的负载约束

依据伊万诺夫的啮合力分布的经验公式[11]，传动载荷作用下啮合力分布如图3所示。

图3中：α为齿形角；qθ为单位宽度齿圈上的周向分布力；qρ=qθtan（α）为径向力；AA′为波发生器长轴，CC′是通过最大载荷值的轴线；φ1表示分布载荷峰值轴线CC′和波发生器长轴AA′的夹角；φ2和φ3确定啮合区大小。角φ由轴线AA′开始按波发生器转向一致为正。qθ沿φ的方向为正；qρ向外为正。

在角φ2和φ3对应的区域内，

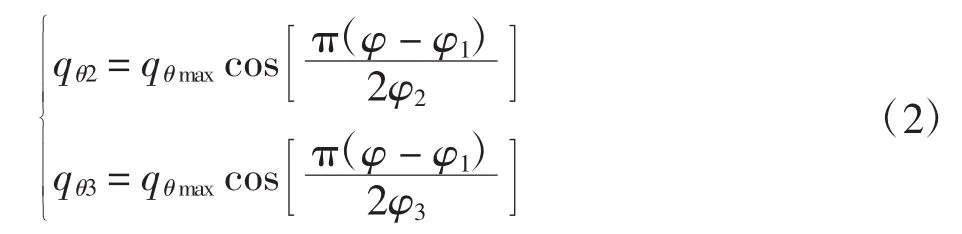
图3 传动载荷作用下柔轮的啮合力分布示意图Fig.3 Meshing force distribution on flexspline teeth

若φ2和φ3相等，那么φ2角区域内，负载扭矩

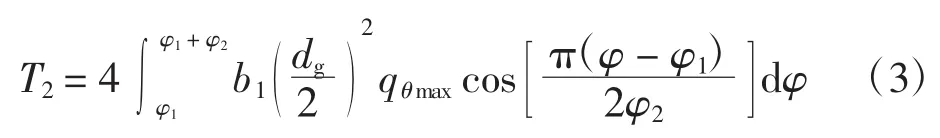
式中：b1为齿圈宽度；dg为分度圆直径，积分得

基于式（2），选择柔轮齿圈中面上、齿圈中间截面的所有结点，设总数为N，则每个结点间夹角f0=360/N。取 φ1=-15°，φ2=-37.5°，φ3=7.5°，根据

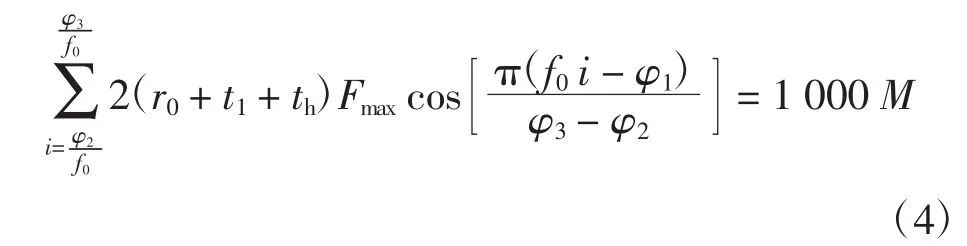
反算Fmax的值。参考HD公司25系列的CSG柔轮，取式（4）等号右边M为最大负载转矩369 N·m。负载转矩下的有限元模型如图4所示。

图4 负载转矩作用下的有限元模型Fig.4 Finite element model in transm ission state

2 结构参数对应力的影响

由于柔轮杯底应力无法用理论方法求解，本文利用ANSYS软件的APDL语言，建立变厚度杯底的柔轮参数化模型。通过最高应力的参数敏感性分析，对关键几何参数分别寻优。然后建立优化杯底厚度的优化模型，进一步降低杯底装配应力和负载应力。

2.1 齿圈周向弯曲应力和杯底装配应力

取长径比l/d0（d0=2r0）从0.1到0.6变化，按国家规范[19]计算齿圈装配应力，并用有限元方法计算杯底的装配应力，如图5所示。

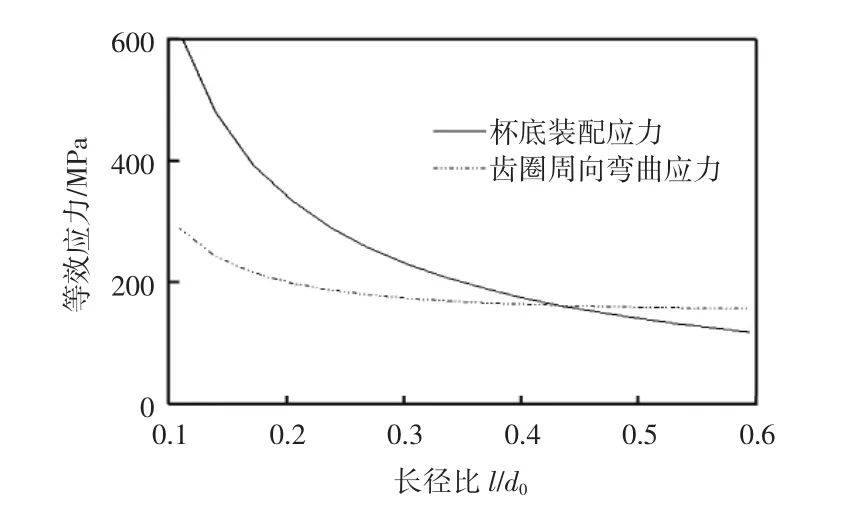
图5 齿圈应力和杯底装配应力与长径比的关系Fig.5 Relation between tooth ring stress and diaphragm stress w ith ratio of length to diameter

图5中，实线和虚线分别为装配状态下杯底的最高等效应力和齿圈部位的周向弯曲应力。从图5可知，波发生器作用下，柔轮杯底最高应力和柔轮齿圈最高应力柔轮随长径比的减小呈单调递增规律。柔轮杯底应力的增幅最大，呈指数级增长，表明柔轮杯底最高应力对长径比的减小更敏感；当长径比小于0.44时，杯底应力超过齿圈应力。我国规范仅给出周向弯曲应力的计算方法，没有给出杯底应力的设计方法。但是，对超短筒柔轮，杯底应力是结构分析和设计的关键问题。

在超短筒条件约束下，筒长的减少会引起杯底装配和负载应力的急剧升高。下面基于长径比l/di=0.4，研究单一改变两个倒圆半径r1、r2和膜板宽度l1对杯底最高装配应力和负载应力的影响。

2.2 筒壁倒圆半径对柔轮杯底最高应力的影响

计算筒壁倒圆半径从r1/ri=0.033～0.16时，杯底结构分别在装配状态和负载工况下的最大等效应力如图6所示。

从图6中看出，随筒壁倒圆半径r1增大杯底最大等效应力线性单调递增，应力从176.3 MPa增长到229.9 MPa，增加了30.4%。可以看出，柔轮筒壁倒圆半径r1对杯底最大装配应力影响较大。当筒壁倒圆半径r1较小时，膜板宽度长，杯底吸收变形的能力好，因而最高应力小；而当筒壁倒圆半径r1增大时，膜板宽度相对减少，杯底吸收变形能力减弱，造成最高应力增大。

最大装配等效应力随r1增大线性增长，应力值从623.3 MPa到638.5 MPa，变化不大。对比图6装配应力和负载应力发现：杯形柔轮的最高负载应力约为最高装配应力的300%。

图6 最高装配应力和负载应力与筒壁倒圆半径的关系Fig.6 Relation between the maximum assembly stress and transm ission stress w ith fillet radius near cup bottom

2.3 膜板倒圆半径对柔轮杯底最高应力的影响

取柔轮最小装配应力值对应的r1/r0=0.033，其他参数不变。计算膜板倒圆半径从r2/r0=0.013～0.140时杯底最大装配应力和最大负载应力，如图7所示。

图7 最高装配应力和负载应力与膜板倒圆半径的关系Fig.7 Relation between the maximum assembly stress and transm ission stress w ith fillet radius near diaphragm

从图7中可以看出，杯底最大装配应力随膜板倒圆半径r2增大呈单调递增状态，且斜率略有上升。当r2/ri=0.013～0.140时，杯底最大装配应力从176.1 MPa增至278.8 MPa，增大了58.3%。当r2/ri越大，引起杯底膜板与凸缘倒角处的杯底厚度增大，使等效应力变大。负载应力的变化规律正好相反。当r2/ri=0.016～0.147时，曲线从623.3 MPa降至458.3 MPa，降低了26.5%。

无论装配应力，还是负载应力，柔轮杯底最大应力对于膜板倒圆半径r2较敏感，对杯底最高应力变化有很大影响。

2.4 杯底最高应力和膜板宽度的关系

基于柔轮应力与筒壁倒圆半径r1、膜板倒圆半径r2的关系。当杯底应力最小时对应的r1/ri=0.033、r2/ri=0.023，其他参数保持不变。计算膜板宽度与筒长的比值l1/l=0.140～0.385时，杯底的最高装配应力和最高负载应力，如图8所示。

图8 杯底最高装配应力和负载应力与膜板宽度的关系Fig.8 Relation between the maximum assembly stress and transm ission stress w ith the diaphragm w idth

图8中，杯底最高装配应力随膜板宽度l1增大单调下降。膜板宽度和筒长比l1/l=0.121～0.385时，最高应力从888.4 MPa降至174.4 MPa。随l1增大到l1/l=0.211时，杯底最大负载应力先急剧下降，后下降斜率变小。这是因为当l1/l很小时，膜板宽度小，导致筒壁倒圆部分吸收的变形增多，因而产生高应力。

3 变厚度杯底的柔轮优化模型

3.1 变厚度杯底的柔轮结构

图9所示为变厚度杯底的控制参数示意图。

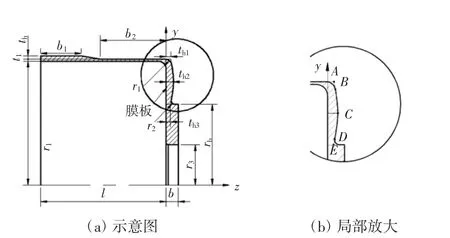
图9 变厚度杯底的控制参数示意图Fig.9 Diagram of parameters of variable thickness bottom

图9（b）中，A、C、E为变厚度杯底曲线的3个控制点。A点为样条曲线和柔轮筒外壁交点，其坐标为（ri+t1，th1）；E点是样条曲线和杯底凸缘外圆的交点，其坐标为（rb，th3），rb是杯底凸缘外半径；C点y向坐标是A、E的中点，其坐标为（（rb+ri+t1）/2，th2）。A、C、E 3点由各自z向坐标th1、th2、th3控制，B点为样条曲线和壁厚倒圆r1的切点，D点为样条曲线和膜板倒圆r2的切点。

3.2 基于三次样条曲线插值拟合杯底剖面

选用三次样条曲线拟合柔轮变厚度杯底。当th1、th2、th3确定后需要给出参数样条曲线的函数表达式，再通过二分法解得样条曲线与杯底2个倒圆的切点，进而连接外筒壁、倒圆和样条曲线，得到杯底曲线。设A、C、E点的坐标分别为（y1，z1）、（y2，z2）、（y3，z3），根据曲线插值定义，AC段方程

CE段方程

式中：a1、b1、c1、d1、a2、b2、c2、d2为待定的8个系数。将A、C、E点的坐标值代入相应式中，得

此外，根据三次样条在公共点处二阶导数连续光滑的条件

为满足8个未知系数的求解，还需2个条件。一般来讲，在曲线的两端，即A、C点各加一个边界条件。根据柔轮筒的特点，选择两端点的二阶导数已知的自然边界条件，得

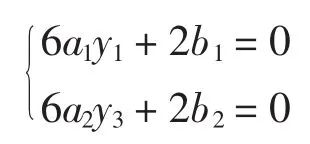
凑齐包含8个未知系数的8个方程。这条曲线可由th1、th2、th33个变量控制。

3.3 确定样条曲线杯底的优化模型

以杯底最高等效应力EQV_BOTMAX作为优化目标f（x*），根据样条曲线表达的变厚度杯底的柔轮模型可知，f（x*）本质上是由th1、th2、th3决定。因此优化目标

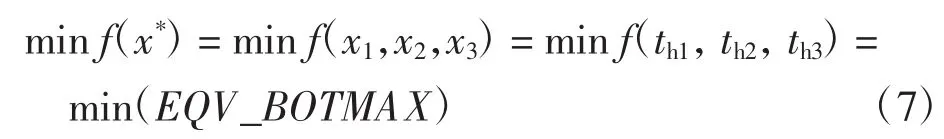
式中：th1、th2、th3为优化模型的优化变量。

由于只有3个点控制样条曲线的变化，当任意相邻的2个点在z轴方向位置相似，而第3个点在z轴方向超过这2个点很多时，杯底曲线和杯底内壁会发生干涉，导致模型错误。有必要约束th1，th2，th3的取值区间。取如下约束

4 优化结果及验证

令th1=th2=th3=0.48 mm，即等厚度杯底，其余参数按表1取值生成模型，计算出杯底最高装配应力180.6 MPa。和前述l/di=0.4方案的结果对比，数值完全吻合，表明样条曲线变厚度杯底可替代等厚度杯底模型。前节分析几个结构参数对杯底最高装配应力和最高负载应力的影响，已找到最高应力最低的结构方案。本节将依据曲线变厚度杯底继续优化最高装配应力和负载应力。

通常使用的优化设计求解方法有：解析方法和数值方法。因本文设计变量少，仅有一个约束，故选择复合形法求解。根据复合形法思想，设计变厚度杯底装配应力和负载应力的APDL优化程序。在每次判断生成新的复合形顶点且需要调用宏程序计算杯底应力之前，先用PARSAV命令保存参数，在宏程序初始位置再用PARRES读入保存的参数。

4.1 装配状态的优化结果

经历262次迭代计算后，杯底最高装配应力收敛至151.8 MPa，如图10所示。

图10 杯底最高装配应力优化过程Fig.10 Optim ization process of the maximum assembly stress

和初始方案相比，应力降低15.9%。图10中左侧坐标轴是最高装配应力，而右侧坐标轴为3个变量th1、th2、th3变化范围。优化后th1=1.212 97 mm，th2=0.480 00 mm，th3=0.773 79 mm。

4.2 负载工况的优化结果

历经88次迭代计算，得到最大瞬时转矩作用下的杯底最高负载应力的最优解349.9 MPa，如图11所示。

与初始方案相比，下降43.9%。最优解th1=2.70859 mm，th2=0.806 46 mm，th3=1.535 18 mm。

4.3 优化方案的应力分布云图

图12为装配应力优化后柔轮的装配应力分布。

由图12可知：优化后的杯底靠近筒壁倒圆处很厚，凸缘附近厚度超过膜板中间。杯底最高装配应力出现在杯底长轴方向的膜板中间。

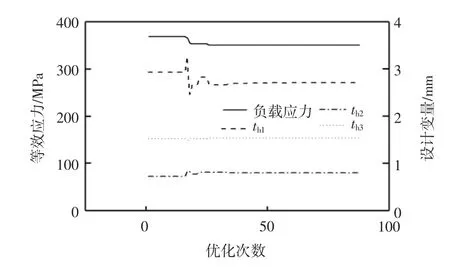
图11 杯底最高负载应力的优化结果图Fig.11 Optim ization process of the maximum transm ission stress

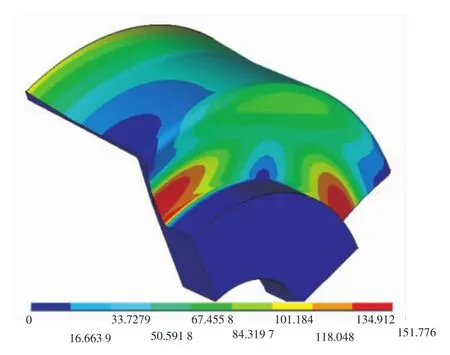
图12 最优方案的柔轮装配应力云图Fig.12 Assembly stress distribution in optim ized flexspline

图13为负载应力优化后柔轮的负载应力分布。

图13 最优方案的柔轮负载应力Fig.13 Transm ission stress distribution in optim ized flexsp line

由图13可见：优化后的杯底靠近筒倒圆处非常厚，凸缘附近的比较厚，膜板中间的厚度超过装配状态的厚度。杯底最高负载应力发生在筒内壁和膜板的倒圆部分。

4.4 基于内置的零阶和一阶优化方法验证

零阶优化方法又称为子问题逼近方法，仅需要因变量的数值而不需要其导数。因变量（即目标函数和状态函数）先通过最小二乘拟合值近似，进而将有约束极小化问题用罚函数转化为无约束问题，在近似的罚函数上连续迭代极小化的过程。

一阶优化方法导数信息进行优化。通过罚函数将有约束优化问题转换成无约束问题，接着对目标函数及状态变量的罚函数进行导数计算，形成搜索方向。在每个迭代步进行最速下降以及对偶方向搜索直到结果收敛。每次的迭代由多个子迭代组成，其中包括搜索方向以及梯度计算。因此和子问题逼近方法相比，一阶优化方法虽然更精确，同时也需要更多的计算量。