模型未知动态场景下移动机器人的视觉镇定

李宝全，尹成浩，师五喜

（天津工业大学 电气工程与自动化学院，天津 300387）

视觉作为人类获取信息的重要感官之一，人类每天从视觉图像中获得大量的信息。视觉传感器是机器人的重要传感器，再加上其非接触式测量、成本低等特点，应用范围越来越广泛[1]。最近几十年对于移动机器人的研究有了前所未有的发展，比如：宇宙探索、深海勘探以及家庭服务等[2]。然而，视觉伺服技术在实际应用中还有许多问题亟待解决。对应现实中都是三维场景，投影到摄像机中成为了二维图像，这就导致了深度信息的缺失[3]。因此，对于单目移动机器人来说，重建3D场景是有困难的。此外，轮式移动机器人是一个典型的具有非完整性约束的欠驱动系统[4]。如Brockett[5]所述，任何连续不变状态反馈控制器都无法实现对非完整系统的稳定控制。为了处理姿态调节中非完整约束，文献[6]设计了平滑的时变控制器来控制机器人移动到期望位姿处。以上这些限制使视觉镇定控制成为控制领域比较困难的任务之一，在动态场景下完成镇定控制变得更具挑战性。

在过去几年，许多研究人员关注了机器人的视觉伺服问题，并且取得了丰硕的成果。传统的视觉伺服方案一般是为6自由度的机械臂设计的，比如在文献[7]中，利用整个图像的光度信息来计算交互矩阵，使得该方法对遮挡和高光场景具有鲁棒性。在文献[8]中，根据从中央折反射系统图像平面中获得的直线投影控制一个6自由度机械臂。在特征点固定不移动的情况下，上述方法对于机器人机械臂的控制是有效的。其他一些控制方法，比如基于图像矩、图像亮度、整幅图像以及直线等特征，仍需要在视觉特征静止的情况下完成工作。如果在动态场景中移动机器人视觉系统仍能完成镇定控制，它们会变得更加智能并能更好地适应环境变化。因此，需要设计一种新的策略以解决动态场景下的视觉镇定控制问题。

与机械臂相比，安装有视觉传感器的移动机器人系统，其应用领域变得越来越广泛。当前，移动机器人视觉伺服实现的主要功能是：利用实时的视觉信号进行反馈以控制移动机器人的运动，最终使机器人到达指定的位姿处或跟踪设定的轨迹。轮式移动机器人本身固有的非完整性限制，使得控制器的设计相比机械臂更加困难。此外，为了将视觉目标保持在相机视野中，文献[9]提出了一种主动视觉的方法。在文献[10]中，通过设计非线性观测器来检测相机的运动范围信息。移动机器人的视觉镇定控制一般利用固定的特征点的当前图像和期望图像之间的误差来获得实时的位姿。如果特征点变动，那么将导致镇定控制任务失败。

尽管当移动机器人在执行轨迹跟踪任务时[11]，特征点是动态的，但这与镇定控制不是一个问题。比如，Liu等[12]设计了一种快速筛选异常值的方法并且利用未校准的全景摄像机来完成视觉回归任务。文献[13]提出了一种基于自适应的视觉伺服跟踪控制的方法。虽然特征点在动态环境中，但这些是属于跟踪控制，不能用于镇定控制。为了处理镇定控制中未知的深度信息，视觉伺服系统通常引入自适应补偿机制[14]。Fang等[15]利用深度信息未知并且模型未知的特征点，通过单应矩阵获得位姿误差，基于Lyapunov稳定原理设计了自适应线性控制器，最终解决了视觉伺服镇定问题[16]。Zhang等[17]提出了一种单应矩阵快速分解获到含有未知比例因子的机器人位姿的方法。但这些镇定控制任务是在特征点保持固定不变的情况下进行的。

本文基于单目轮式移动机器人，设计了一种可在动态场景中利用模型未知的特征点完成视觉镇定控制的策略。本方案大致有分为以下步骤：首先，在实验场景中引入一个固定的监视摄像机，通过获取的信息可以得到不同场景下深度信息的比例；然后，通过包含未知特征深度的信息获得极坐标表示下的运动学模型，再利用单应矩阵分解和坐标系变换来计算移动机器人当前姿态与期望姿态之间实时的相对关系；最后，采用自适应控制器驱动机器人到期望位姿处。

1 问题描述

1.1 系统描述

控制系统由移动机器人和车载摄像机组成。视觉伺服任务的坐标系关系如图1所示。

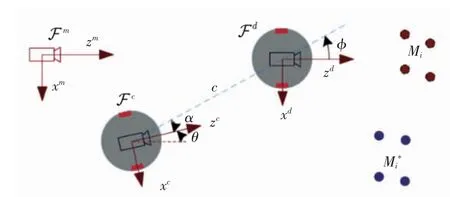
图1 视觉伺服任务的坐标系关系Fig.1 Coordinate systems relationship of the visual servoing task

1.2 控制方案

图2所示为视觉伺服策略框图。

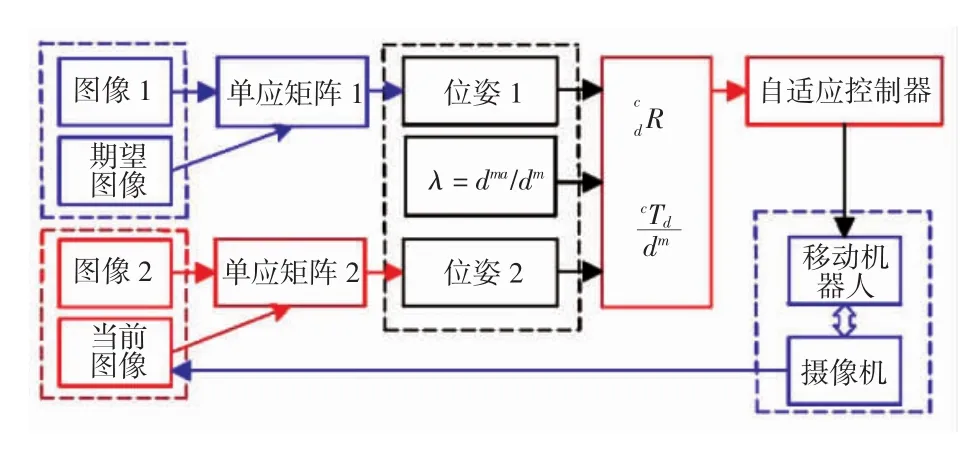
图2 动态场景下视觉伺服策略图Fig.2 Block diagram of visual servoing strategy under dynam ic environment

图2中：图像1表示特征点移动前在监视相机中的图像；图像2表示特征点移动后在监视相机中的图像。整个视觉伺服策略为：

（1）期望图像是将移动机器人事先放到期望位姿处获得，它与图像1可以估计出第1个单应矩阵。因此利用六自由度的单应矩阵分解[22]，可得到监视摄相机位姿与期望位姿之间旋转矩阵和平移向量

（2）在视觉伺服过程中，针对移动后的特征点，利用车载视觉系统获得的当前图像与图像2结合可以得到第2个单应矩阵。与第一步类似，可以得到机器人当前坐标系与监视相机坐标系之间旋转矩阵和平移向量

（3）无论特征点移动前还是移动后，场景的深度信息均为未知，并且特征点移动前后场景深度信息不相同。考虑到这一点，文中利用特征点与视觉图像之间的几何关系，计算出该2个不同深度信息之间的比例λ。

（4）根据坐标系变换规则，实时地计算出机器人当前位姿与期望位姿之间的旋转矩阵和平移向量进而采用自适应控制器将轮式移动机器人驱动到期望位姿处。

1.3 坐标系关系的表示

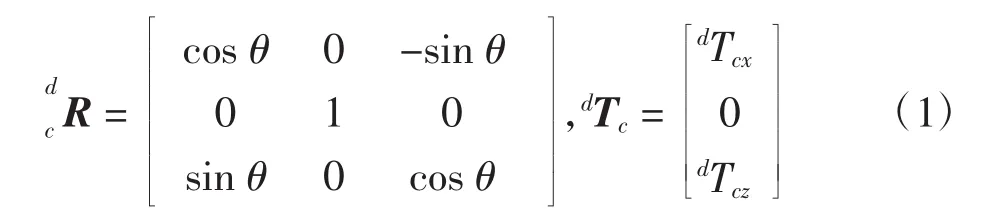
1.4 图像表示

在空间中有4个共面的动态特征点Mi（i=1，2，3，4），并且表示移动之后的特征点。期望图像、当前图像、图像1和图像2的第i个像素点的表示分别是，具体表示如下：

2 控制策略

本节计算出轮式移动机器人的期望位姿与当前位姿之间实时相对关系。

2.1 监视相机与期望位姿的关系

式中：h（it）是一个与深度比有关的系数表示单应矩阵表示如下摄像机内参数矩阵：

式中：（u0，v0）表示图像的主点；（fu，fv）为用像素块表示的焦距。射影单应矩阵G（t）可以通过最小二乘法获得。因此，单应矩阵得到如下：

通过对期望图像和图像1得到的单应矩阵分解[22]，可以得到监视相机与期望位姿之间的相对关系。由于可以分解出8种不同的结果，经过算法筛选之后可以得到2个有效解，再根据实际的物理模型确定用哪一组解。最终得到的旋转矩阵和平移向量如式（6）所示：

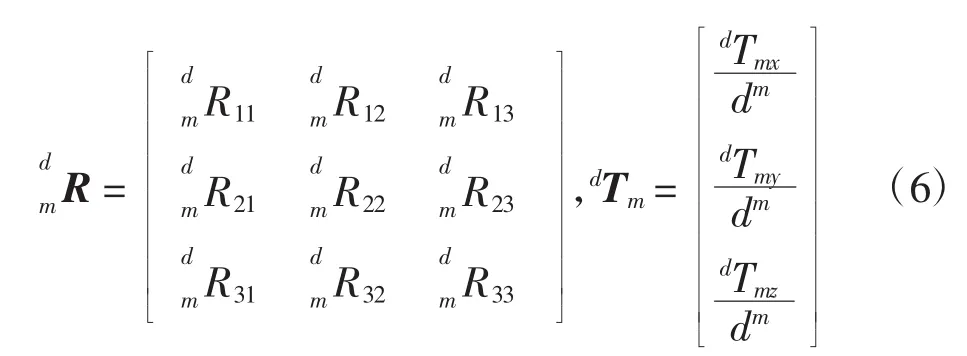
式中：dm表示从坐标系m的原点沿平面的法向量nm到特征点平面的未知深度。

2.2 监视相机与当前位姿的关系

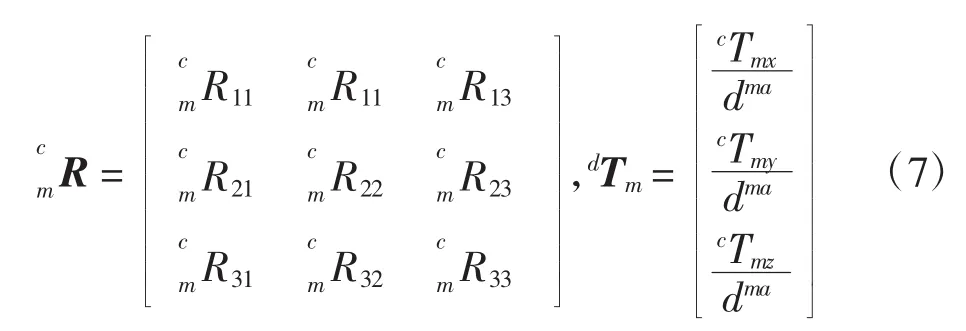
式中：dma表示从坐标系m的原点沿平面的法向量nma到移动后特征点平面的未知深度。

2.3 两个未知深度信息之间的比例因子

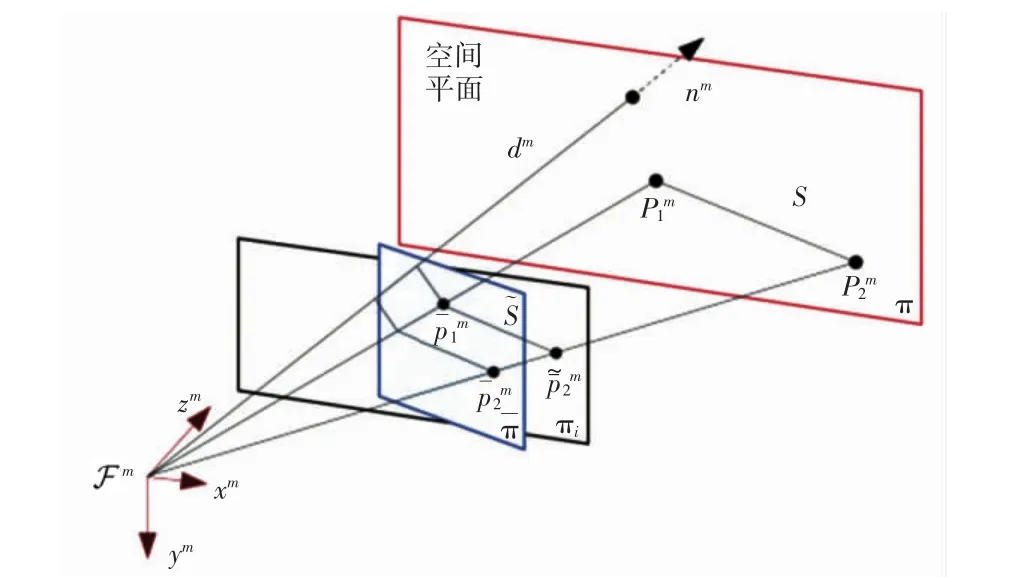
图3 深度信息dmFig.3 Diagram show ing the distance dm

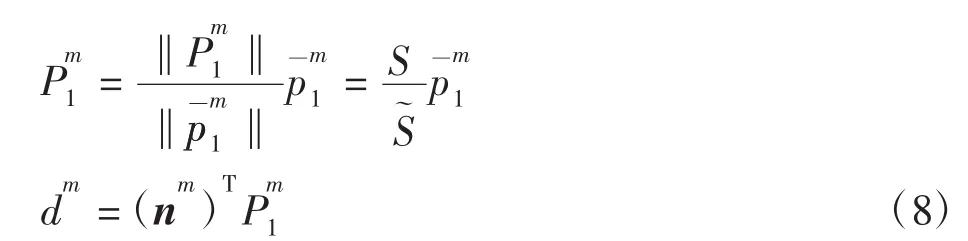
当特征点移动后，特征点和深度信息也发生了相应的改变。因此变成了同样地，可以表示如下：

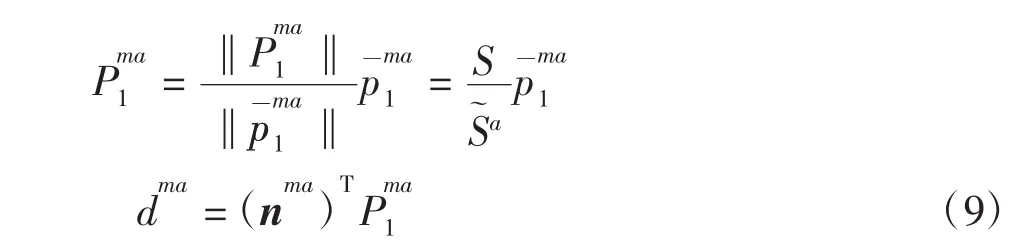
由式（8）和式（9）可以计算出不同深度信息之间的比例：

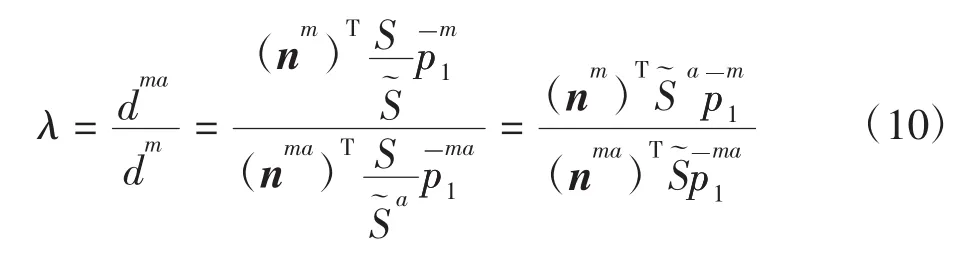
2.4 当前位姿与期望位姿的关系

经过以上计算，监视相机位姿与机器人期望位姿之间的关系可以表示如下：

移动机器人的当前位姿与监视相机位姿之间的相对关系为：

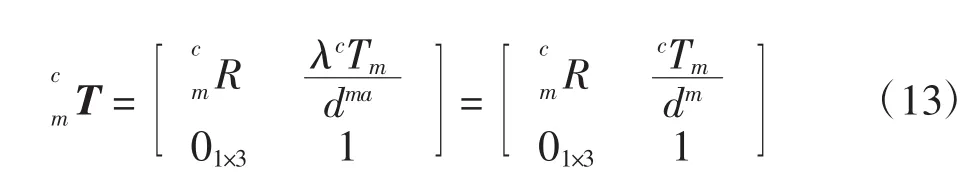
因此通过坐标系变换可以得到实时的移动机器人当前位姿与期望位姿之间关系：

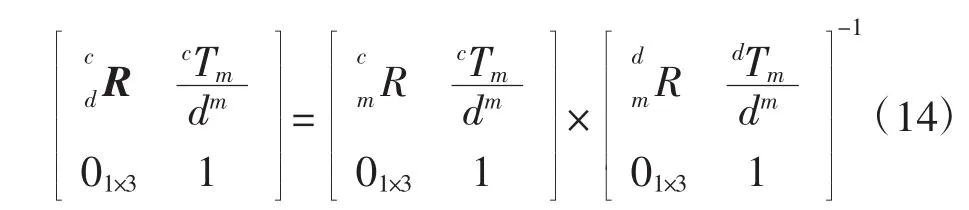
3 驱动机器人到期望位姿

为了使控制器的设计更加方便，将机器人在笛卡尔坐标系下的位姿转换成极坐标下的表示[20]。将的范数定义为当前位姿与期望位姿的距离误差e（t），表示为由于深度信息dm和dma是未知的，所以e（t）是不可以直接测量出来。因此，将含有比例因子的可测距离误差e（st）定义为：

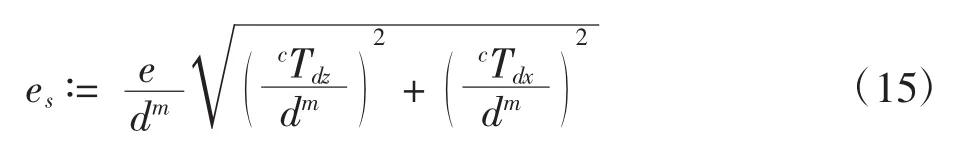
角度 φ（t）和 α（t）可以表示为：

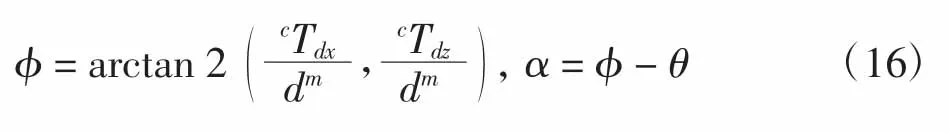
3.1 运动学模型

基于极坐标的机器人运动学模型表示为

根据系统需要将其重新定义为：

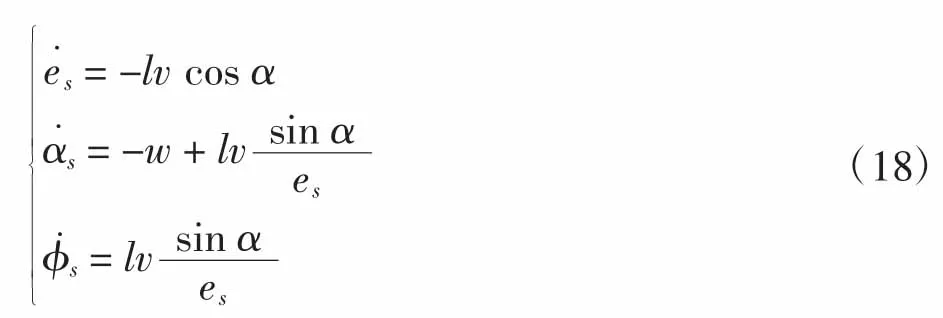
3.2 自适应控制器

由于深度信息是未知的，可以通过采用一个自适应控制器[18]来完成镇定控制任务。基于Lyapunov稳定原理，通过利用可获得的信号设计机器人的线速度和角速度为：

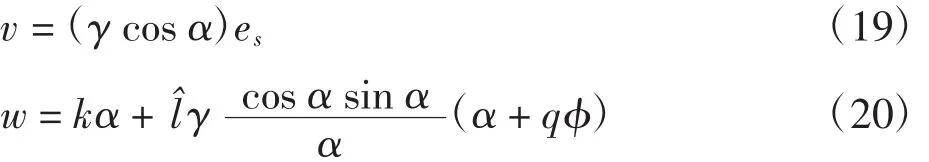
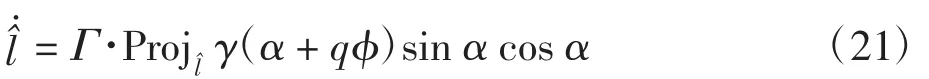
4 仿真及实验结果

4.1 仿真结果

为验证所提方案的可行性，首先在MATLAB上搭建模型进行仿真实验。在仿真场景中设置了4个共面特征点，并且设置了移动后的特征点。仿真中的虚拟相机内参数设置为：

图4为机器人的位姿变化的仿真结果。

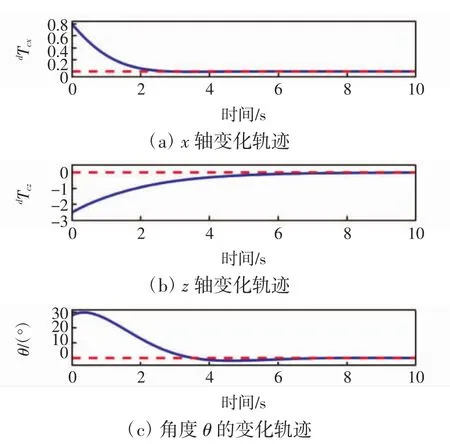
图4 机器人的位姿变化的仿真结果Fig.4 Simulation results of evolution of robot pose

图5为移动机器人实时的线速度和角速度的仿真结果。

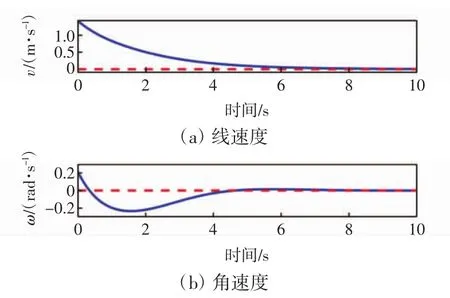
图5 机器人的线速度和角速度的仿真结果Fig.5 Simulation results of linear velocity and angular velocity of mobile robot

由图5可见，随着时间的变化，线速度和角速度都趋于零，说明机器人镇定到期望位姿时，可以停止运动。

图6为特征点图像轨迹图。

图6 特征点图像轨迹图的仿真结果Fig.6 Simulation results of image trajectories of features

图6中显示的是特征点在图像中的变化轨迹，图中的圆点表示初始位姿时刻的特征点图像坐标，正方形表示的是机器人到达期望位姿时特征点在图像中的位置，星形是特征点移动前在期望位姿处的图像位置。由于特征点的移动，所以星形没有与正方形重合。

图7为机器人在三维空间中的移动路径的仿真结果。

图7 机器人移动轨迹的仿真结果Fig.7 Simulation results of mobile robot motion trajectory

4.2 实验结果

经过仿真之后，进行实验以进一步验证所提方法的有效性，实验场景如图8所示。

图8 实验场景Fig.8 Experiments scene

图8中，实验用的是带有车载摄像机的IN-R型移动机器人，绿色棋盘格面板为共面特征点，左下角为固定的监视相机。本文方法是在配备有OpenCV库的VC++6.0环境下实现的。

以期望位姿作为参考坐标系，将初始位姿随机设置在-2.2 m，0.6 m，32°，所以期望位姿为0.0 m，0.0 m，0°。选择的控制增益参数为

首先将移动机器人放置到期望位姿采集期望图像，如图8所示的机器人进行采集图像，然后将机器人随机放置到其他位置（初始位姿），与此同时特征点做了相应的移动（模拟特征点受到外界较大干扰）。

图9为监视相机捕获的图。图9（a）是移动机器人在期望位姿时，监视摄像机捕获的未发生变化的特征点图像，图9（b）是移动机器人在初始位姿处时，监视摄像机捕获的发生变化的特征点图像。

图9 监视相机捕获图Fig.9 Images of feature points in monitor camera

图10为特征点在摄像机中的图像变化。由图10可见图形的表示方法与仿真中叙述的一致。移动机器人的实时的变化如图11所示。

图10 特征点图像轨迹图的实验结果Fig.10 Experimental results of image trajectories of features

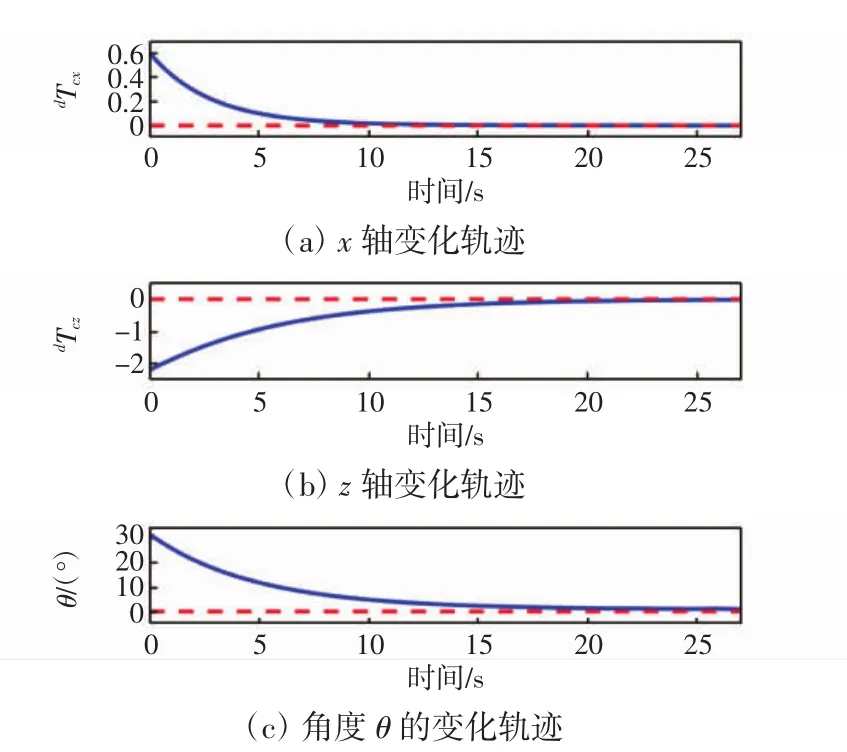
图11 机器人的位姿变化的实验结果Fig.11 Experimental results of evolution of the robot pose

图11中，红色虚线是期望值，蓝色线为实际的值，可以看出3条轨迹逐渐趋于期望值。

图12为试验中移动机器人的线速度和角速度变化，由图12可见，线速度和角速度最终都趋于零。

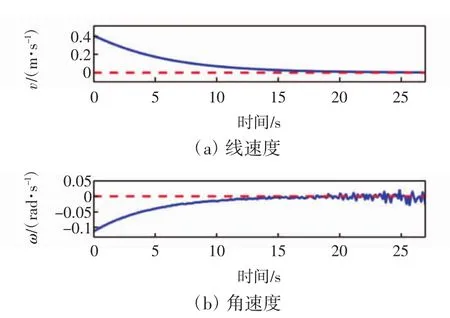
图12 机器人的线速度和角速度的实验结果Fig.12 Experimental results of linear velocity and angular velocity of mobile robot

图13为移动机器人从初始位姿到期望位姿的路径。图中，红三角是期望位姿处，可见机器人最终镇定到了期望位姿处。实验表明所提出方法具有可行性。

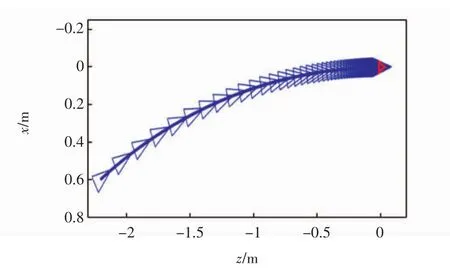
图13 机器人移动轨迹的实验结果Fig.13 Experimental results of motion path of mobile robot

5 结论

本文针对移动机器人在镇定控制中特征点不能移动的问题，提出了一种处理动态场景下的视觉伺服策略，并且场景中特征点的3D模型是未知的。首先，利用单应矩阵分解方法计算出期望位姿与监视相机之间的关系；然后利用同样的方法计算出当前位姿与监视相机之间的关系。由于场景的变化导致深度信息的不同，所以需要得到两者之间的比例，以用来将平移向量转变成含有同一个深度信息；再结合坐标系变换算出实时的当前位姿与期望位姿之间的关系；最后，采用一个自适应控制器将机器人驱动到期望位姿处。仿真和实验结果表明：环境发生变化时，移动机器人可以完成镇定控制，即随着时间变化，在位姿误差e→0的同时，线速v→0和角速度w→0，此时机器人镇定到期望位姿处。通过与传统镇定方法的仿真和实验对比研究发现：

（1）传统的视觉镇定控制一般利用固定的特征点完成镇定任务。

（2）本文所使用的方法，在场景深度信息未知，特征点3D模型未知的情况下完成动态场景下的视觉伺服镇定控制，从而提高了移动机器人环境适应的能力。