非线性失真影响下的OFDM系统压缩感知信道估计算法

丛连日，刘振栋，武 侠，丛旖旎，戈立军

（1.国网山东省电力公司 烟台供电公司，山东 烟台 264001；2.天津工业大学电子与信息工程学院，天津 300387）

正交频分复用（orthogonal frequency division multiplexing，OFDM）具有频带利用率高、抗符号串扰能力强、抗频率选择性衰落能力强等优点，是当前高速无线通信领域的核心，亦是未来5G移动通信的物理层核心调制技术[1-5]。在OFDM系统中，信道估计的精度直接影响衰落信道下的系统性能[6]，而信号的高峰均比与器件线性度的不足将导致信号产生非线性失真（nonlinear distortion，NLD）[7]。在未来的5G当中，尤其对于高频段高速无线通信，低成本硬件的发展需求使系统引入硬件受限影响，由此带来的器件非线性因素将会使系统的信道估计性能恶化[8-10]。

目前国内外已有大量关于OFDM信道估计的研究[11-15]，由于无线信道多具有稀疏性，基于压缩感知（compressive sensing，CS）的信道估计研究成为近年来的热点。然而，现有方法多数未考虑非线性因素的影响。近年来，随着无线通信技术的发展，已有部分学者开始关注NLD影响下的OFDM信道估计问题[16-18]。在非线性OFDM系统中，基于带有NLD的辅助信息难以估计出准确的信道信息，而衰落信道同时又制约NLD的估计与消除，信道与NLD相互影响成为存在NLD时进行信道估计的难点。文献[16-17]提出一种迭代联合算法，利用最小二乘（least squares，LS）和离散傅里叶（discrete Fourier transform，DFT）插值方法进行信道估计，利用判决反馈和信号重构方法进行NLD消除。该联合算法的估计性能受限于导频数量和判决精度，且需已知限幅先验信息，信号重构操作亦造成系统具有较高的复杂度。文献[18]提出基于线性最小均方（linear minimum mean-squared error，LMMSE）和压缩感知的迭代联合算法，其计算复杂度较高，且需已知信道先验信息。本文针对存在NLD的OFDM系统的信道估计问题，利用信道与NLD的双重稀疏性，提出一种适用于非线性OFDM系统的压缩感知信道估计算法。在发射机中进行导频分组与级联限幅，在接收机中利用消除NLD影响的第1组导频进行压缩感知信道估计，利用消除信道影响的第2组导频进行压缩感知NLD估计。该方法考虑了非线性对信道估计的影响，在接收机中对信道和NLD进行分组估计，可避免系统实施降低峰均比算法，且无需已知任何先验信息，同时无需进行迭代计算。

1 非线性OFDM系统模型

发射机中经IDFT调制所得OFDM时域信号为[9]

信号经信道传输到达接收机，接收信号为[9]

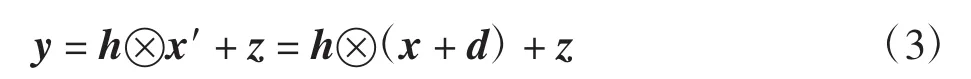
经DFT解调所得频域信号为[19]

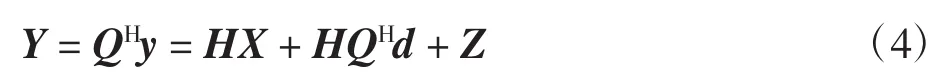
2 联合算法

在非线性OFDM系统中，导频信号会产生NLD，若直接利用带有NLD的导频进行信道估计，将导致系统性能急剧下降。为解决此问题，本文首先提出在发送端分组导频与级联限幅方案，以保护导频信息不受非线性失真影响，进而利用信道与NLD噪声的双重稀疏性，在接收端提出基于压缩感知的信道与NLD联合估计方法。

2.1 分组导频与级联限幅

为利用压缩感知同时估计信道与非线性失真，设计2组梳状导频：第1组用于信道估计，定义为向量为信道估计导频组长度；第2组用于NLD估计，定义为向量其中R为NLD估计导频组长度。为消除信道估计导频组所受NLD的影响，提高信道估计精度，本文在传统限幅法基础上提出在系统发送端进行级联限幅，以减小限幅带来的导频处NLD噪声。

对时域OFDM信号xn进行限幅，求限幅失真噪声

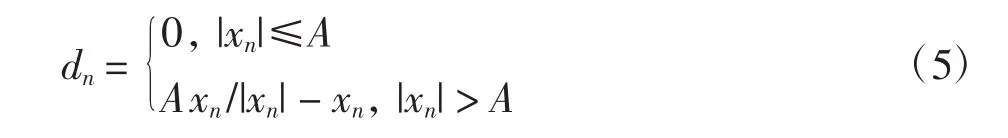
式中：QH为傅里叶变换矩阵。将D中与信道估计分组导频位置相对应的元素置为0得到D′，以消除NLD噪声影响，再将D′变换到时域

上述频域置零操作会使第1次限幅后的信号产生一定程度的峰值回升，需对其进行第2次限幅使不超过门限值A。

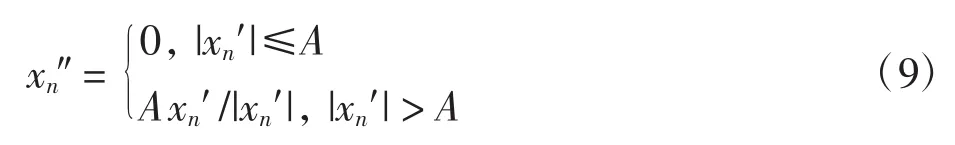
设2次限幅产生的NLD噪声为d″，则2次限幅后的信号可以表示为

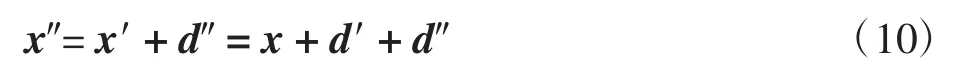
第2次限幅会使频域信道估计导频处重新产生NLD，但此时的NLD噪声影响已大幅减小。若重复执行式（5）—式（8）的过程，可以进行多级级联限幅，但本文第3部分的仿真表明2次级联限幅即可达到较理想的去噪效果。

2.2 基于压缩感知的信道与NLD估计

接收端首先基于分组导频XpCE进行信道估计，再以信道信息为先验信息利用分组导频XpNLDE估计信号的非线性失真。将（10）式代入前文信号模型（3）式后进行傅里叶变换可得

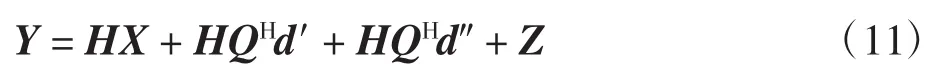
选取信道估计导频所在的行可得

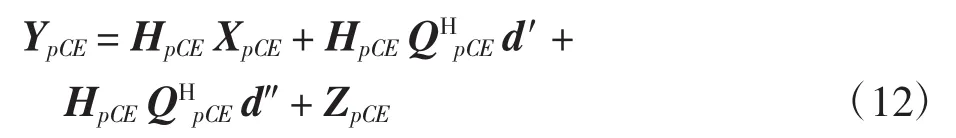
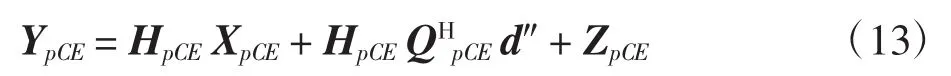
由于第2次限幅后导频处的噪声影响已很小，这里将上式第2项归并到噪声项中，则

进一步整理为压缩感知基本形式，上式改写为

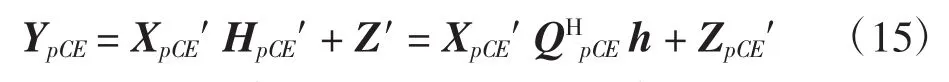
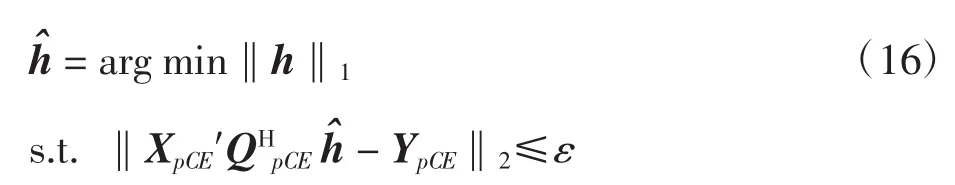
本文采用贪婪类重构算法正交匹配追踪（orthogonal matching pursuit，OMP）算法[20]对上式中的h进行求解，以同时获得较好的性能与较低的复杂度。

将上式改写为

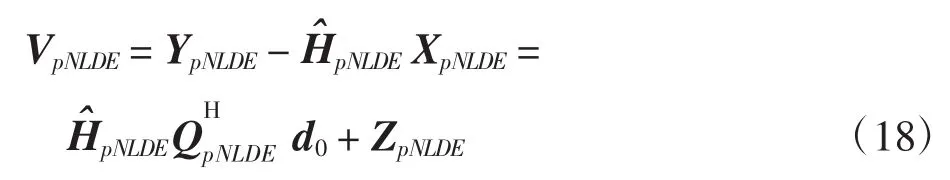
同样利用压缩感知求解NLD噪声d0，即

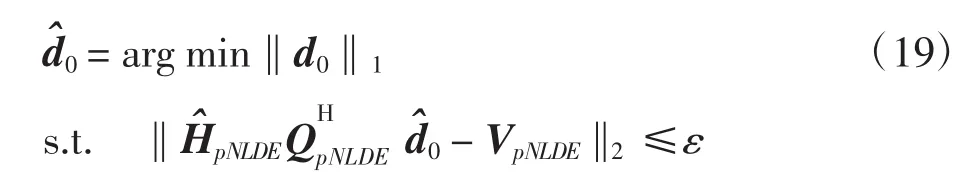
本文仍采用现有的OMP算法对上式中的d0进行求解，从而估计出系统中的NLD噪声。

3 仿真分析

为验证本文算法性能而搭建的OFDM系统包含512个子载波，其中包括70个导频子载波，循环前缀长度为64，采用64QAM调制及5/8 LDPC编码，离散信道长度为42，有6个有效径。

对于分组导频算法来说，导频组合方式会极大影响算法的性能，对于不同的应用场景，导频的组合方式没有确定的形式与规律，需要通过实验的方式确定。经过多次仿真，在本文的仿真中，当用于信道估计的导频数为22、用于非线性失真估计的导频数为48时，系统可以达到较好的性能，所以本文算法仿真的导频组合方式为22+48。

图1为限幅门限为2.5 dB不同限幅次数在不同信噪比下的算法联合估计均方误差性能。由图1可见，随着信噪比的增大，算法性能逐渐提高，2次限幅与3次限幅的性能明显优于1次限幅，而在2次限幅与3次限幅情况下，算法性能十分接近。

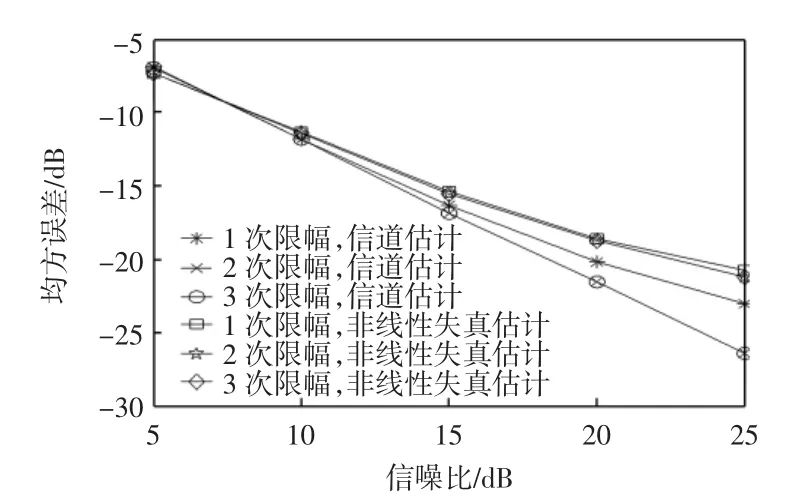
图1 不同信噪比下的压缩感知联合估计性能Fig.1 Performance of joint compressed sensing estimation under different signal-to-noise ratios

图2为信噪比25 dB时不同限幅次数在不同限幅门限下的联合算法均方误差性能。由图2可知，随着限幅门限的升高，算法性能逐渐提高。同样，1次限幅性能最差，2、3次限幅性能相似。综合上述结论可知，本文算法在2次限幅情况下已经达到较优的性能。在信噪比为25 dB、限幅门限为2.5 dB条件下，2次限幅后的信道估计均方误差约为-26.3 dB，非线性失真估计误差约为-21 dB。在后续仿真中，系统均采用2次级联限幅。

图2 不同限幅门限下的压缩感知联合估计性能Fig.2 Performance of joint compressed sensing estimation under different lim iting thresholds

图3、图4分别为限幅门限2.5 dB、不同联合算法在不同信噪比下信道估计和非线性失真估计性能。从图3和图4可以看出，随着信噪比的增加，不同方法的估计性能逐渐提高，而本文提出的方法在信道估计和非线性失真估计两个方面均具有较低的均方误差性能。当信噪比较高时，本文方法的信道估计性能优于对比文献的方法，且接近理想的压缩感知估计性能。

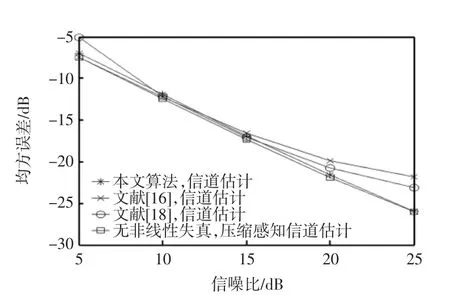
图3 不同信噪比下的信道估计性能Fig.3 Performance of channel estimation under different signal-to-noise ratios

图4 不同信噪比下的非线性失真估计性能Fig.4 Performance of NLD estimation under different signal-to-noise ratios

图5、图6分别为信噪比为25 dB，各算法在不同限幅门限下的信道估计和非线性失真估计性能图。

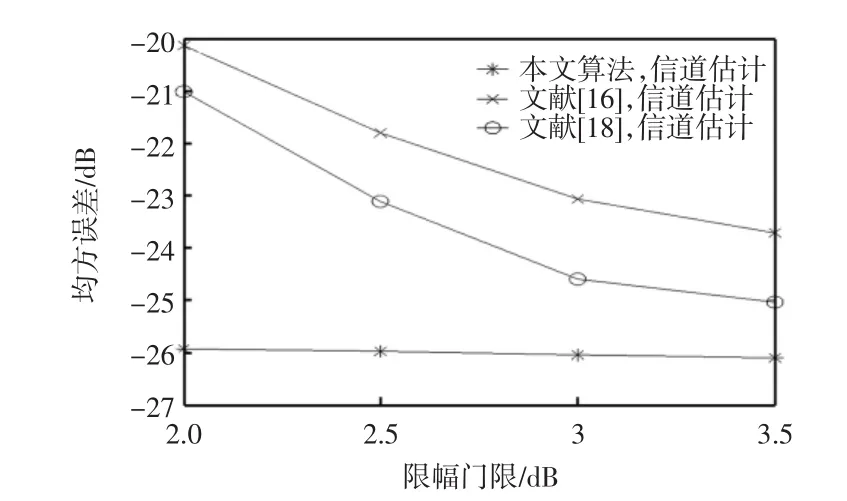
图5 不同限幅门限下的信道估计性能Fig.5 Performance of channel estimation under different lim iting thresholds

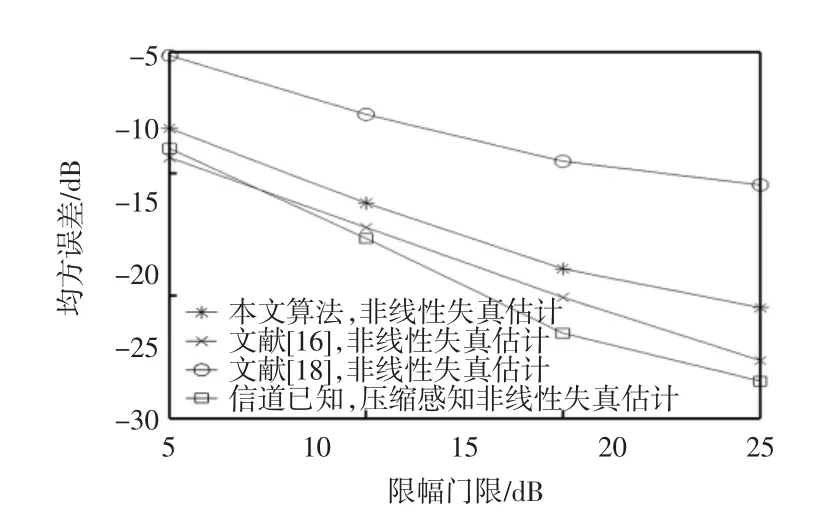
图6 不同限幅门限下的非线性失真估计性能Fig.6 Performance of NLD estimation under different lim iting thresholds

由图5可知，当信噪比较高时（大于15 dB），本文算法的信道估计性能明显优于文献算法，且十分接近无非线性失真的压缩感知信道估计性能。在信噪比为25 dB、限幅门限为2.5 dB条件下，本文方法的信道估计均方误差相比于传统方法改善了约3～5 dB。这是由于级联限幅保护了用于信道估计的导频不受非线性失真影响，同时压缩感知信道估计在稀疏信道下比LS+DFT和LMMSE方法更具优势。由图6可知，本文算法性能优于文献[18]而劣于文献[16]。因为同样利用压缩感知进行非线性失真估计，本文算法中作为观测矩阵的信道估计值比文献[18]更精确；而由于非线性失真信号的稀疏度与限幅门限值有关，故基于压缩感知的非线性失真估计性能对限幅门限敏感，而符号重构的方法则不受稀疏度的影响。

4 结论

本文针对非线性失真影响下的OFDM系统信道估计精度下降的问题，提出适用于非线性OFDM系统的压缩感知信道估计算法。该方案考虑了非线性失真对系统的影响，在接收机中对信道和NLD进行估计，无需已知先验信息与迭代运算。仿真表明，在信噪比较低时，该算法性能略高于其它算法但较为接近。在信噪比较高时，该算法具有明显优于其它算法的估计性能。在信噪比为25 dB、限幅门限为2.5 dB条件下，该方法的信道估计均方误差约为-26 dB，相比于传统方法改善了约3～5 dB。