高速剑杆织机共轭凸轮引纬机构运动精度分析

袁汝旺，刘 瑀，周国庆，龚文强

（天津工业大学 天津市现代机电装备技术重点实验室，天津300387）

剑杆织机引纬形式主要包括共轭凸轮引纬[1]、空间四连杆引纬[2]和变螺距引纬[3]等，剑杆运动平稳性与纬纱交接可靠性是其关键[4]，其中共轭凸轮引纬机构因其稳定性高与适应性强被广泛应用[5-6]。为满足织机高速的需求，研究机构运动精度误差与织造工艺的关联机制逐步受到重视。张雷等[7]建立考虑间隙与尺寸误差的空间连杆引纬机构运动精度计算模型，分析各个因素对运动精度的影响程度；唐雪梅等[8-10]研究基本尺寸误差、间隙及凸轮磨损等因素对剑杆织机共轭凸轮打纬机构可靠性的影响。共轭凸轮引纬机构由滚子摆动从动件凸轮机构、铰接四杆机构与齿轮机构等组成，国志刚等[11]建立盘型凸轮摆杆角位移误差的计算模型，分析精度误差影响因子；陈建军等[12-13]研究平面铰接四杆机构的运动精度可靠性；黄贤振等[14-16]分析尺寸误差对啮合角位移影响并建立了齿轮运动精度模型；亦有学者[17-19]研究机械系统的运动精度分配机制，并提出精度分配方法[20]，但对复杂多机械系统的机构运动精度误差建模方法及其误差分配机制的研究尚显不足。

本文以共轭凸轮引纬机构为研究对象，建立含尺寸误差与运动副间隙的剑杆织机引纬机构运动精度误差模型，结合概率统计方法分析影响运动误差的主要因素，并探讨引纬工艺与机构运动精度误差的关系，为共轭凸轮引纬机构的优化设计与制造提供一定的理论依据与技术参考。

1 共轭凸轮引纬机构工作原理

图1所示为共轭凸轮引纬机构工作原理。

图1 共轭凸轮引纬机构运动简图Fig.1 Conjugate cam weft insertion mechanism kinematics diagram

由图1可知：共轭凸轮1匀速转动，通过与其接触的转子驱动转子臂往复摆动，连杆4与转子臂固结，并通过连杆5与摆杆6带动扇形齿轮往复摆动，扇形齿轮通过齿轮8、9、10以及剑带轮11带动剑杆水平往复运动。共轭凸轮1、转子2，2′与转子臂3，3′组成凸轮机构，转子臂连杆4、连杆5和摆杆6组成铰接四杆机构，扇形齿轮、齿轮8、9、10组成齿轮机构，且凸轮机构、连杆机构、齿轮机构与剑带轮串联组成传剑系统，驱动剑头按照一定规律进行往复运动，实现纬纱交接。

2 共轭凸轮引纬机构运动精度建模

考虑尺寸误差与运动副间隙对凸轮机构、铰接四杆机构与齿轮机构运动精度误差的影响，建立共轭凸轮引纬机构的运动精度模型，并分析各机构对剑杆运动特性的影响程度。

2.1 考虑尺寸误差的机构运动精度模型

2.1.1 考虑尺寸误差的凸轮机构运动精度模型

图2所示为滚子摆动从动件凸轮机构运动关系。

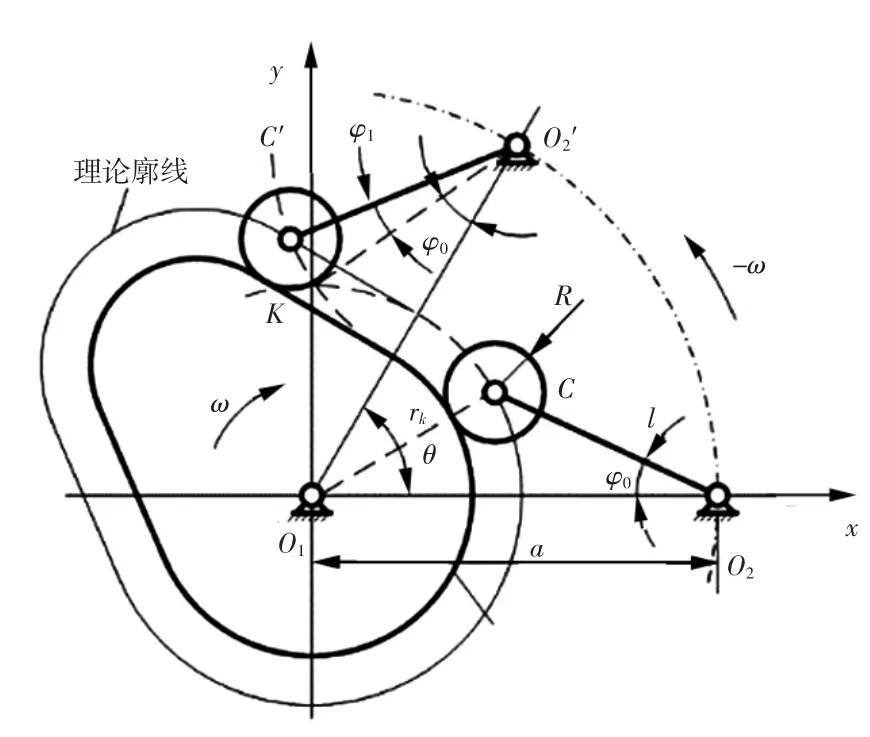
图2 凸轮机构运动关系Fig.2 Diagram of cam kinematics

当凸轮以角速度ω匀速转动时，凸轮摆杆摆角

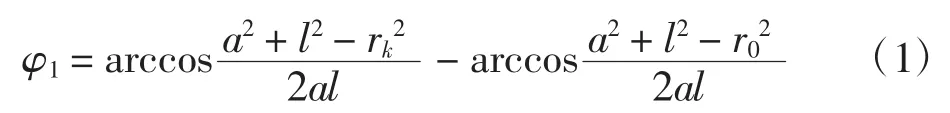
式中：a为中心距；l为摆杆长度；rk为与凸轮转角θ对应的理论廓线向径；r0为理论廓线基圆半径。

考虑凸轮机构尺寸误差时，摆角误差为

式中：Δa为中心距误差；Δl为摆杆长度误差；ΔR为滚子半径误差；Δrk为实际廓线表面的误差。

2.1.2 考虑尺寸误差的铰接四杆机构运动精度模型

图3所示为铰接四杆机构的运动关系。

图3中，摆杆O2A以角速度ω1转动时，摆杆BO3的角位移

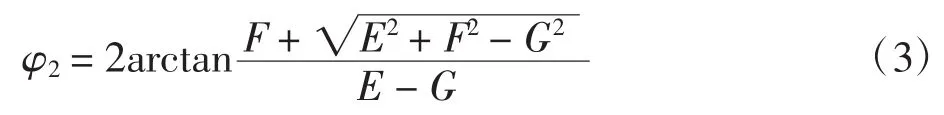
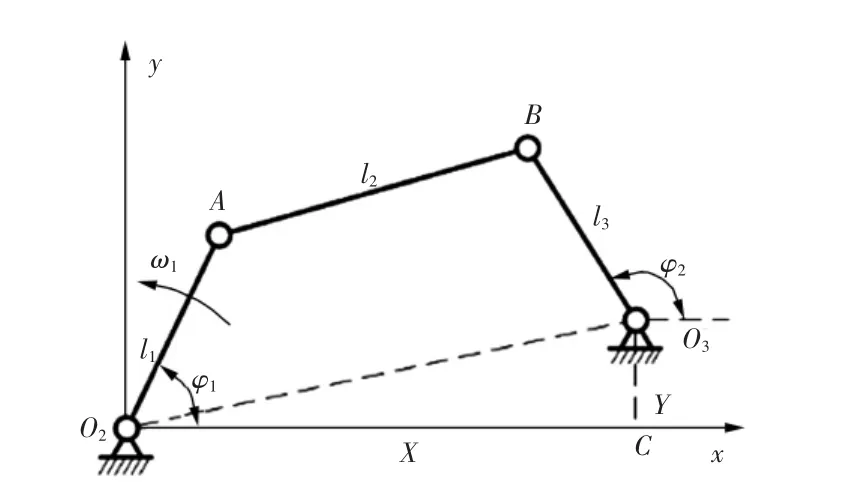
图3 铰接四杆机构运动关系Fig.3 Four-bar linkage movement diagram

考虑机架安装位置误差与杆长尺寸误差时，摆杆角位移误差

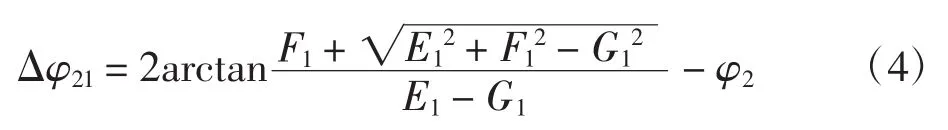
2.1.3 考虑尺寸误差的齿轮机构运动精度模型

由于加工制造等原因造成齿轮回转中心与几何中心不重合，设主动轮几何中心相对于回转中心存在偏距e，图4所示为其传动原理。

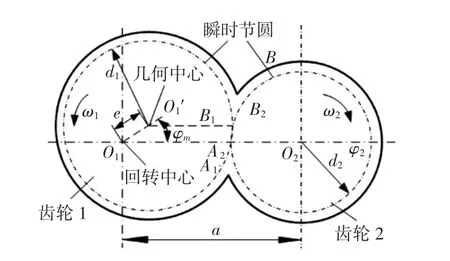
图4 齿轮偏心影响转角误差Fig.4 Influences of gear eccentricity on rotation error

由图4可知：O1为回转中心，O1′为几何中心，中心距a=d1+d2，则齿轮的瞬时传动比：

式中：d1与d2分别为齿轮1和齿轮2的节圆直径。

考虑中心偏心误差的瞬时传动比K′

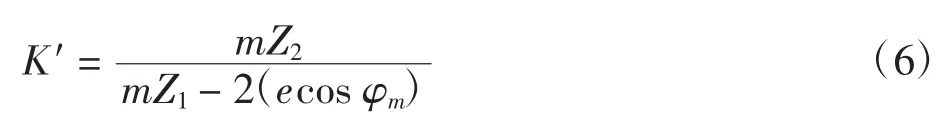
式中：m为齿轮模数；Z（ii=1、2）为对应齿轮齿数；e为偏距；φm为齿轮1的偏心线O1O1′与齿轮副中心线O1O2的夹角。

同理，锥齿轮的计算方法同圆柱齿轮一致，可经过当量齿轮确定。共轭凸轮引纬机构中包含两对齿轮组，图5所示为齿轮组传动示意图。

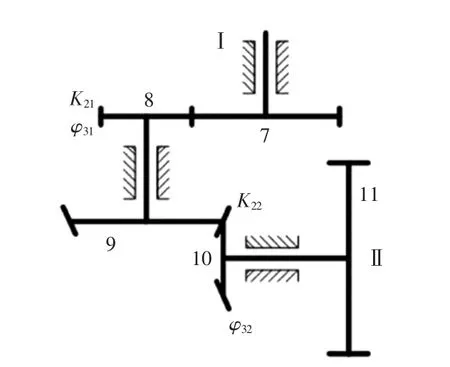
图5 齿轮系统传动示意图Fig.5 Transm ission diagram of gear system

由图5所示，轴Ⅰ为主动轴，轴Ⅱ为输出轴。输出轴运动误差为

式中：Δφ31为齿轮9的角位移误差；φ31为齿轮9的角位移；K21′为齿轮7和齿轮8的传动比。

式中：Δφ32为齿轮10的角位移误差；φ32为齿轮10的角位移；K22′为齿轮9和齿轮10的传动比。

2.2 考虑运动副间隙的机构运动精度模型

2.2.1 考虑间隙的凸轮机构运动精度模型

根据等效杆长理论，运动副间隙影响并改变凸轮摆杆的实际等效杆长。图6所示为共轭凸轮机构中含铰链式运动副间隙的运动模型。

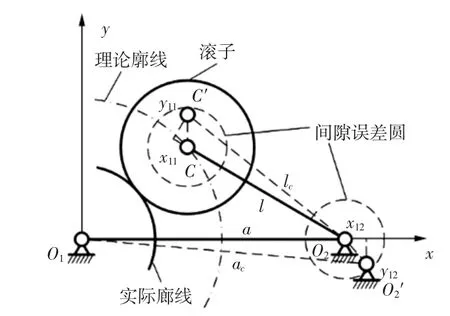
图6 考虑运动副间隙的凸轮运动模型Fig.6 Cam kinematics model considering kinematics pair clearance

凸轮摆杆与滚子和机架分别由铰链副连接，受其径向间隙影响，凸轮摆杆与中心距等效长度为

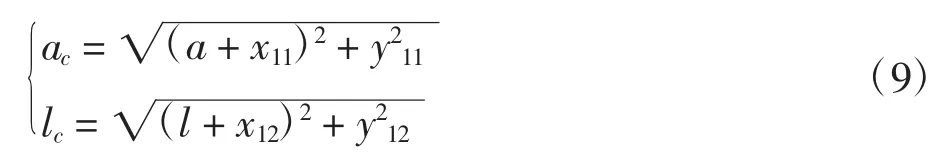
式中：x11与y11为凸轮滚子与摆杆之间的径向间隙；x12与y12为凸轮摆杆与机架之间的径向间隙。

考虑间隙时，摆角误差为

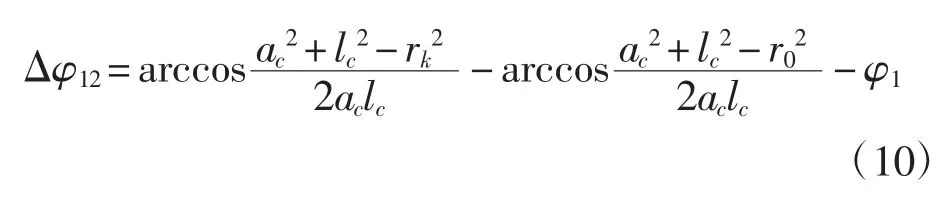
2.2.2 考虑间隙的铰接四杆机构运动精度模型

图7所示为含运动副间隙的铰接四杆机构。

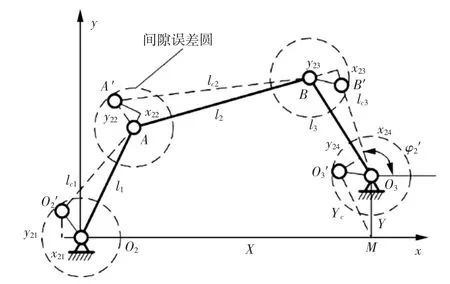
图7 考虑运动副间隙的铰接四杆机构运动模型Fig.7 Consider the articulated four-bar kinematics model of kinematics pair clearance

间隙误差主要来源于铰链副O2、A、B和O3，受铰链副影响的平面四杆机构等效杆长

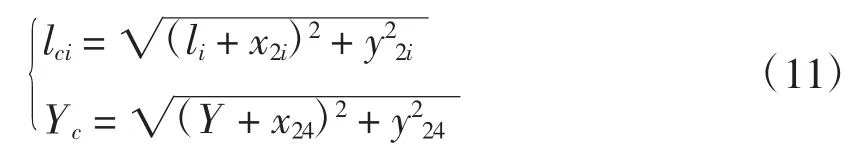
式中：x2i、y2（ii=1～3）为连杆铰链副径向间隙；x24、y24为机架铰链副径向间隙。

考虑间隙时，铰接四杆机构的摆角误差

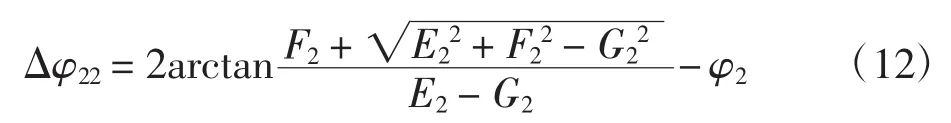
2.3 共轭凸轮引纬机构运动精度模型

织机主轴电机通过减速系统驱动共轭凸轮匀速转动，其输出的变速运动特性经铰接四杆机构、齿轮机构与剑带轮进行放大并实现引纬运动。图8所示为共轭凸轮引纬机构传动路径。

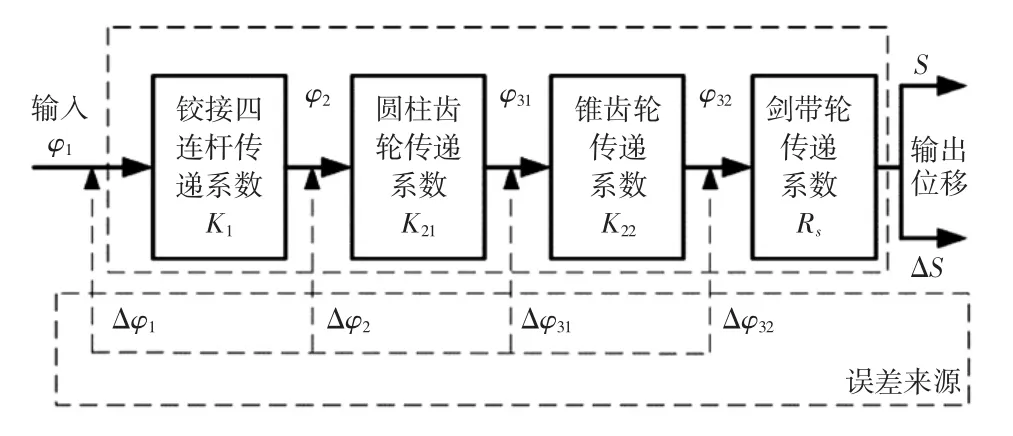
图8 共轭凸轮引纬机构传动路径Fig.8 Diagram of the transm ission diagram of conjugate cam guide

图8中：φ1和Δφ1分别为凸轮摆杆角位移及其误差；φ2和Δφ2为铰接四杆机构摆臂角位移及其误差；φ31和Δφ31为经过圆柱齿轮放大后的角位移及其误差；φ32和Δφ32为剑带轮的角位移及其误差。

根据微小位移叠加原理得到剑头位移总误差

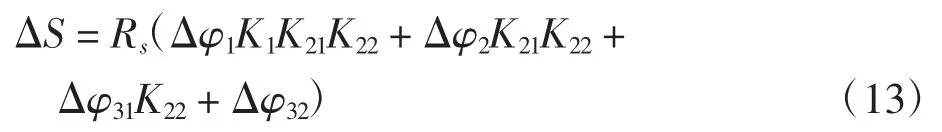
式中：ΔS为剑头位移误差；Rs为剑带轮半径。

3 计算实例分析

3.1 参数选择

织机转速为300 r/min，纬纱交接冲程为60 mm，织物幅宽为2 300 mm，运用表1中给定的机构参数进行运动学仿真分析。

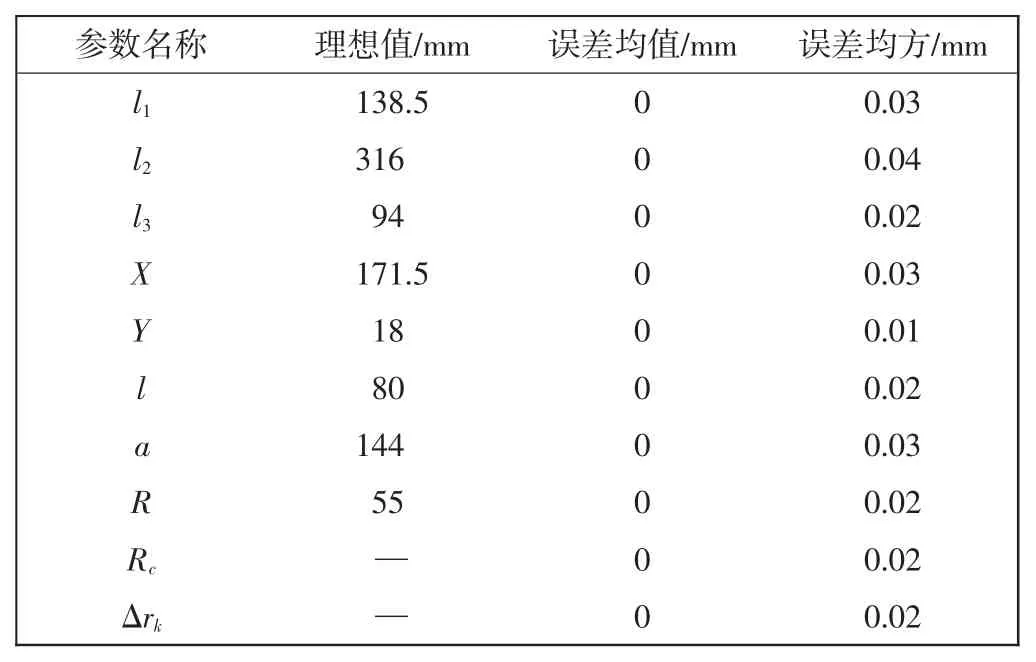
表1 模型参数Tab.1 M odel parameters

3.2 机构误差对剑杆运动精度的影响

为分析尺寸误差和运动副间隙耦合作用对剑杆运动特性的影响程度，建立考虑尺寸误差与运动副间隙同时影响的机构运动精度模型。图9所示为考虑凸轮摆杆误差时剑头的运动偏差曲线。

由图9可知：位移、速度及加速度偏差分布较均匀，波动较明显，呈随机波动的状态。

图10所示为考虑凸轮和连杆误差时剑头的运动偏差曲线。

由图10可知：位移曲线的范围增大，且方差增大较明显，波动增大；速度曲线的范围和方差均有小幅度增加；加速度的变化较小，大致持原有水平。

图11所示为综合考虑凸轮、连杆和齿轮三种机构误差时剑头的运动偏差曲线。由图11可知：位移的波动范围增大，且波动剧烈的程度增加；速度波动范围增加较少，但方差有明显增大；加速度在波动的范围及波动程度上，有少量的增加。

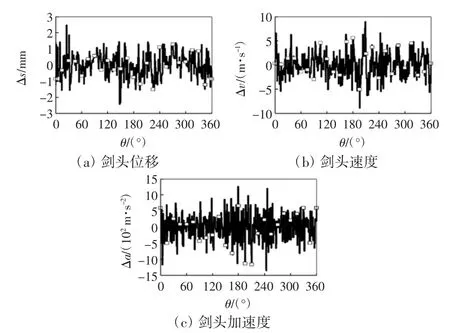
图9 考虑凸轮机构误差时剑头运动偏差曲线Fig.9 Sword movement deviation curves considering error of cam mechanism separately

图10 考虑凸轮机构与铰接四杆机构的误差时剑头运动偏差曲线Fig.10 Sword movement deviation curvesconsidering error of cam mechanism and four-bar mechanism

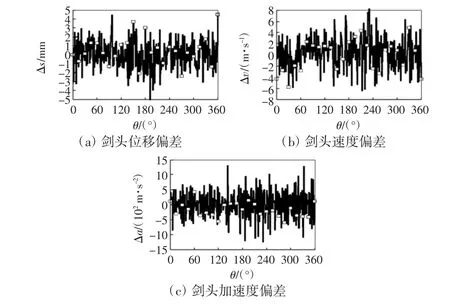
图11 考虑凸轮机构与铰接四杆机构及齿轮机构的误差时剑头运动偏差曲线Fig.11 Sword movement deviation curves considering the error between cam and four-bar mechanism and gear

表2所示为图9—图11的位移偏差统计结果。

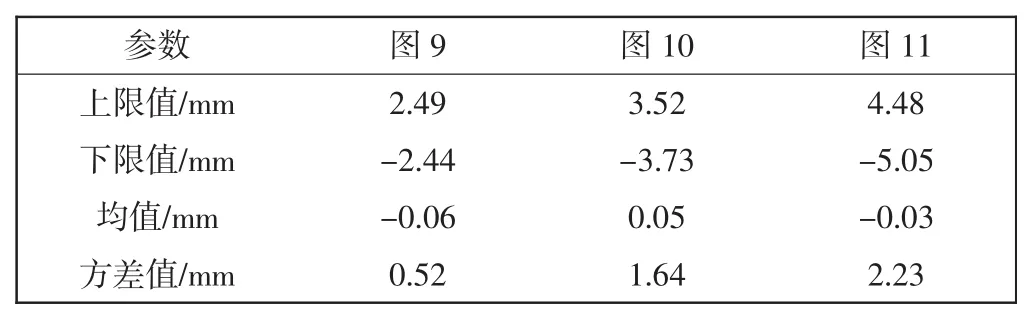
表2 位移偏差统计结果Tab.2 Statistical deviation statistical results

由表2可知：凸轮、铰接四杆机构和齿轮机构对剑头位移误差影响的占比分别约为48%、35%和17%，即凸轮机构误差对剑头位移影响最大。将凸轮机构加工精度提高2个等级，即凸轮摆杆长度、中心距、凸轮滚子半径及凸轮向径加工的误差均方均为0.01 mm，图12所示为精度提高后的剑头运动特性曲线。

图12 提高凸轮机构加工精度后的剑头运动偏差曲线Fig.12 Deviation of characteristic curves of sword head after machining precision of cam mechanism is improved

由图12可知：位移、速度和加速度波动的最大值分别为4.4 mm、4.57 m/s和8.38×102m/s2，提高凸轮机构加工精度对降低剑头运动精度误差作用明显。

3.3 运动精度误差对引纬工艺的影响

图13所示为共轭凸轮引纬机构剑头运动特性曲线。

图13 剑头运动特性曲线Fig.13 Characteristic curves of sword

由图13可知：剑头运动规律为改进梯形，当织机主轴转角θ=72°时剑头进入梭口，并在θ=180°时达到最大位移，纬纱交接过程在接纬剑转角处于200°～220°范围时进行，此时送纬剑转角处于140°～160°范围中。随后开始退剑，当θ=288°时，剑头退出梭口；当主轴转角在θ=130°和θ=250°附近时，剑带运行速度达到最大，而在θ=180°时剑带运行速度最小。

图14所示为纬纱交接原理。

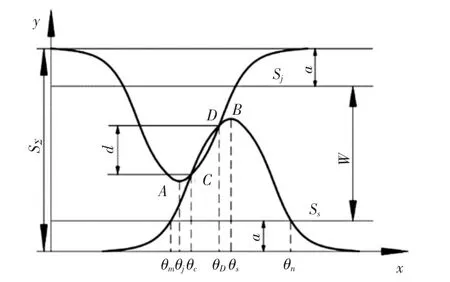
图14 纬纱交接示意图Fig.14 Transition diagram of weft

图14中：Sj和Ss分别为接、送纬剑的运动轨迹；A、B两点分别为接、送纬剑的进足位置；C、D两点为纬纱的交接冲程；a为剑杆幅外动程；W为筘幅宽度。接、送纬剑运动规律一致，接纬剑比送纬剑提前20°到达进足位置。

由图12可以看出：剑头进入与退出梭口时产生的位移偏差分别为4.08 mm和-3.28 mm，会使得剑头进出梭口的时间发生改变；速度偏差值分别为5.88 m/s和3.29 m/s，加速度偏差值分别为-8.07×102m/s2和11.7×102m/s2，剑头进出梭口时易产生震动，从而引起经纱断头；在纬纱交接过程中，位移偏差为-4.09～3.23 mm，两剑头产生振动容易出现交接失误；两剑相遇后，送、接纬剑保持同向运动，速度偏差造成相对速度不稳定，容易出现钩断纬纱，造成交接失误；加速度的偏差均值为13.07×102m/s2，且运动精度误差致使剑头运动的最大加速度提高约40%，产生的惯性力和动态变形较大，交接时造成冲击较大，不利于纬纱交接。

4 结论

（1）考虑尺寸误差与运动副间隙的因素，分别建立凸轮机构、铰接四杆机构与齿轮机构的运动精度模型及其串联组成的共轭凸轮引纬机构运动精度误差模型。

（2）分析凸轮机构、铰接四杆机构与齿轮机构误差对共轭凸轮引纬机构剑头运动特性的影响，确定凸轮机构在剑头位移误差影响中占比最大，约为48%，可通过提高凸轮机构加工精度与凸轮转子间啮合精度，降低铰链间隙从而改善机构运动特性。

（3）共轭凸轮引纬机构剑头出现-4.9～3.32 mm的位移误差，导致剑头进出梭口的时间发生改变，纬纱交接时出现13.07×102m/s2的加速度误差值，产生较大惯性力与动态变形，导致交接失误。

（4）建立了尺寸误差和运动副间隙对剑杆运动精度影响的模型，为后续揭示尺寸误差和运动副间隙等因素对剑杆运动特性的影响程度提供了理论基础。