波发生器作用下柔轮变形机理的非线性有限元分析*

2015-06-11郭刚，钟健

机械研究与应用 2015年2期

郭刚，钟健

(深圳职业技术学院机电工程学院，广东深圳 518055)

0 引言

谐波齿轮传动技术是近年来发展起来的一种传动技术，其特点是用柔性元件所产生的可控波动变形实现动力的传递。与传统传动机构相比有许多独特的优点比如:运动精度高、回差小、体积小、承载能力高、传动精度和传动效率高等，目前已应用于众多领域中。在当前使用谐波齿轮传动中，应用最为广泛的几种波发生器均是刚性的。为了实现柔轮与波发生器的轮齿间无侧隙啮合，近几年一些专家学者提出了弹性波发生器的概念［1］，这种波发生器的优点在于通过调整波发生器变形力可改变柔轮径向变形量，从而实现上述目的。

若要实现无侧隙啮合，需研究柔轮的变形与波发生器变形力间的关系，及相应的柔轮的形变、应力和应变分布规律，以利用其指导谐波齿轮的设计。为此笔者利用MSC.Patran建立了分析谐波齿轮传动柔轮变形的非线性接触有限元计算模型，详细的分析柔轮在弹性波发生器接触作用下的变形过程和机理。

1 有限元模型

根据常用的双谐波齿轮实际情况，在MSC.Patran中建立了分析模型，并详细的分析了波发生器与柔轮间的相互作用。其中接触状况按非线性处理。

1.1 3D模型的建立与有限元网格划分

按照典型双谐波齿轮机型的参数进行模型的建立。柔轮所选用的材料的牌号为30CrMnSiA，其弹性模量为206 GPa，泊松比取0.3。柔轮实际尺寸及柔轮轮齿部分相关参数如图1所示。

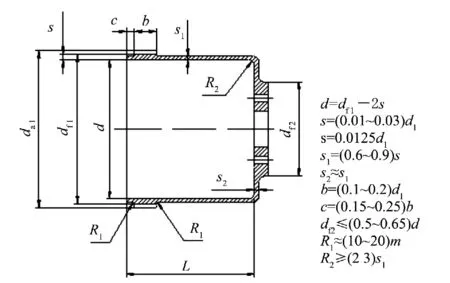
图1 杯形柔轮结构简图和尺寸

建模时为了减少网格划分和计算所用机时，忽略了柔轮底凸缘根部及齿轮根部小圆角，其原因在于文中研究波发生器作用下的柔轮变形，距离该圆角所在位置较远，忽略圆角对计算结果影响非常小。同样柔轮轮齿部分数量多和相对尺寸较小，划分有限元网格时，会造成相对较多的单元数量及增加网格划分的难度，而笔者主要研究柔轮在弹性波发生器作用下的预变形，因此在不影响计算精度的情况下将柔轮轮齿简化为等效厚度的齿圈。

同时，为了进一步减少计算的机时，利用模型的对称性，针对半个柔轮进行计算。网格划分使用八节点六面体实体单元，网格划分后得到约47 000个网格单元。根据实际变形中波发生器相对刚度大，变形很小的特点，将波发生器的作用由一个与波发生器轮廓线和轴向长度相同的刚性圆柱面代替。有限元计算模型如图2所示。

图2 杯形柔轮模型

1.2 施加约束和载荷

位移边界条件:文中研究波发生器作用下的柔轮变形，变形主要发生在柔轮顶部开口端附近。根据实际情况和计算要求限制柔轮底部凸缘表面全部6个自由度，由于利用零件的对称的特点，只计算一半的零件。计算时设定在对称面处周向位移为0。

接触边界:在 MSC.Patran/Marc中设定接触边界，将柔轮设定为变形体，波发生器设定为运动刚体同时给定其径向运动规律。波发生器沿径向向外运动，与柔轮内侧接触，并使柔轮逐渐发生形变。在设定边界条件时给定其位移增量。根据问题的具体情况，计算时忽略两物体间摩擦力。

2 结果和分析

2.1 杯形柔轮位移分布

图3为杯形柔轮计算结果沿刚体运动方向的位移分布图。

图3 杯形柔轮计算结果的位移分布

变形云图显示柔轮的位移变形以波发生器接触的相关区域为界对称分布。杯形柔轮的变形量的量值由开口端向封闭端逐渐减小。波发生器的最大位移是0.39 mm。图3中可看出在波发生器作用下，杯形柔轮的最大位移为0.426 mm，发生在其与波发生器接触的相关区域靠近开口端一侧。表明柔轮产生了轻微翘曲。同时最大变形区域已与运动刚体柱面已脱离接触。而封闭端的变形最小，几乎接近零。