小学数学深度课堂的维度构建

摘  要：数学深度课堂基于儿童立场，以凸显数学本质立深度，以对接生活实践延广度，以关注有效情感增温度，多维度合力促进数学学习的深度发生，实现让课堂“立”起来“立人”。

关键词：深度课堂;儿童立场;数学本质

当儿童与数学在课堂上自然相遇，让儿童的学习深度发生、核心素养得到长足发展就成了数学教师最朴素的课堂追求。而儿童立场、学科本质、深度学习这些不同的维度如何共筑深度课堂，让数学课堂“立”起来“立人”，就成为我们努力实践的方向。

一、深度，凸显数学本质“立”

数学是人类思维的产物。数学经典名著《什么是数学》中写道：“数学作为人类智慧的一种表达方式，反映生动活泼的意念、深入细致的思考，以及完美和谐的愿望。” [1]而写进教材后的数学就是一些客观性、逻辑性和抽象性极强的运算法则、性质、公式、公理等，其所呈现的是一种“冰冷的美丽”，而要实现把“冰冷的美丽”还原为“火热的思考”，就需要抓住数学本质，通过深度对话、深度体验、深度探究等活动，感悟与理解数学最基本的概念、思想方法、思维方式、精神等，从而让教学穿越数学的表层符号，走向意义认同。

1. 概念感悟多元化

小学数学知识体系中概念是最基本的部件，小学阶段的概念学习也是基础中的基础。“概念是人脑对事物本质特征的反映”。就像自然数“1”，现实生活中只有一个苹果、一棵树、一个人、一只小鸟等，并没有“1”，它只是抽象概括后创造出来的数字，因此要让儿童去理解掌握这些概念就需要多元感悟，如从最初的形态上，从应用变化上，从概念间联系上等，多视角全方位感悟理解这些最基本的概念，这样的概念学习就是可联结的、可生长的、可结构化的。

如“百分数的认识”中，安排了这样几个层次的概念感悟活动：首先结合商场里“20%off”的广告牌，初步理解意思;其次是结合自己的理解画一画、写一写表示出“20%”，从而实现与已有经验中的除法、份数、小数、分数、比等进行了对接;第三个活動是结合一些商品的原价看看降价多少，根据多组关于降价和原价的数据去思考“20%”在哪里;最后深度思考“百分数是一种什么样的数”的问题，从而能更好地理解百分数的概念，更好地理解为什么百分数是百分率，又为什么是百分比了。这样多元感悟把概念的建立与生活实际相连，与百分数的发展历史相关，与儿童已有经验相通，在概念的内涵理解上形成最深刻的认识。

2. 方法体验聚焦化

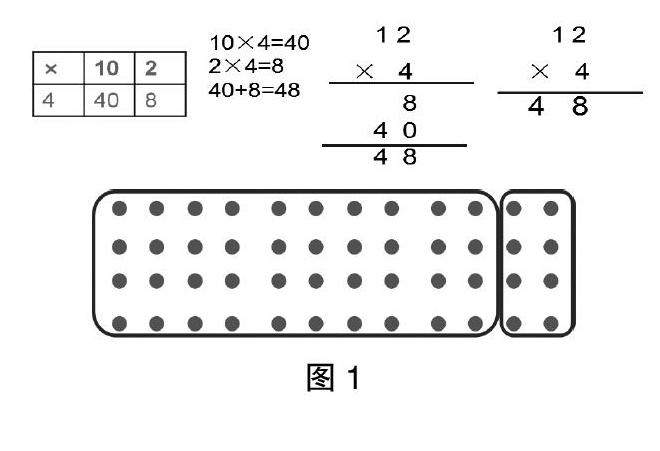
数学思想方法是对一些策略、规律的理性把握与认识。教材在编排中明的是知识掌握这条线，其实在知识后面也暗藏着数学思想方法生长的线索。教学中要通过深度开发挖掘基础知识背后的思想方法，授之以鱼，更授之以“渔”，并通过聚焦这些思想方法的来龙去脉，让学生对数学思想方法能有深度体验，在习“渔”之技时，问“渔”之理，得“渔”之道。如转化思想的学习中，通过对学习或解决问题中的化新为旧、化繁为简、化曲为直、化难为易的整理，聚焦为什么要转化、怎样转化、转化后有什么变化等问题的理解，从而帮助儿童深刻体会到数学思想背后的数学思考。再如教学“12×4”的竖式计算中，先通过点子图对口算、计算中方法背后的算理进行聚焦，由于在点子图中表示出来的想法是一样的，这样“理”相通就呼之欲出。

而当完成竖式的认识后，再次借助点子图聚焦描述12×4竖式发展历史，特别是和以前的印度竖式、铺地锦、国外的竖线计算等对接，使儿童借助直观点子图完美呈现了方法背后所蕴含的乘法分配律。这样不断聚焦，让“法”相联，儿童对方法的体验就更加深刻，对方法背后的算理理解也更加透彻。

3. 精神品鉴常态化

美国数学家M·克莱因说：数学是一种精神，一种理性精神。这种精神就是数学核心素养中提到的“必备的数学品格”。教学中在对“关键数学能力”常态培养的同时，更要注重对数学精神的欣赏与追求，经常引导儿童从哲学层面去思考“为什么这样、还可以怎样”，从理性角度分析问题、解决问题，要多通过思辨帮助儿童常态品鉴数学精神，深度感悟其内涵实质。只有这样，才能不得鱼忘筌，让数学精神之树在课堂上常态栖居，茁壮成长，最终让儿童学会用数学思维去认识世界。如平均数教学中对“1.2米的免票线”的思考：为什么是1.2米、1.2米怎么出来的、为什么不根据年龄而是根据身高等，这些思考就可以引导儿童深度探寻统计中如何进行抽样调查，如何进行数据分析，怎样借助统计数据进行决策等，从而在理性探寻中实现深度认同。

二、广度，对接生活实践“延”

华罗庚先生曾说过：宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。美国统计学家C.R.劳也曾说过：在抽象的意义下，一切科学都是数学。可以说数学在现实生活中应用广泛，但实际上儿童目之所及的数学是教材，用之最多的数学是考试。如果很难看到数学在生活中的应用，当然也就很难感受到数学的价值所在。当下教材不应是儿童的世界，而世界才应是儿童的教材。只有联系生活对接实践，开展真实问题的学习，才能打开一扇扇窗户，让儿童看到世界因数学而秩序井然，生活因数学而更加美好。从而也就能体会到古希腊数学家普洛克拉斯说的：哪里有数，哪里就有美。

1. 举三反一生活化

学会用数学的眼光观察世界是数学重要的核心素养，数学的眼光是要会“抽象”，要能从生活原型中发现其本质特征。而注重数学眼光的培养不能缘木求鱼，应本着举三反一的策略，提供丰富的生活素材。让儿童通过观察与对比、想象与联想、类比与类推的过程，去练就一双“慧眼”，实现用数学的眼光去把世界看得清清楚楚、明明白白。如认识分数的教学中安排了以下的活动，首先是通过一张长方形纸平均分成4份去认识 ，然后是动手把这张纸裁开，看还能不能看到这几个分数;其次用分数讲龟兔赛跑的故事，结合看情境去认识分数;最后通过“下课了”“谢谢同学们”，结合看文字再去认识分数，从而实现从数学的角度对“万物皆数”的实质认同。

2. 自内生外具体化

数学知识是高度抽象概括的，往往简洁的数学表达背后简缩了很多数学事实，而教材限于篇幅也没法呈现这么多的事实。教学中要深度解读数学背后的生活事实，并联系这些生活事实把抽象的数学具体化。

就像这道最被人诟病的题：“有一个水池，打开进水管注满水池要3小时，打开出水管放完整池水要2小时。现在同时打开进水管和出水管，要多少时间才能把一池水放完？”甚至被春节联欢晚会上的相声讽刺，引得哄堂大笑。却不知数学学习的只是抽象后的模型，如果结合生活举举例子就能明白，类似这样一边进水一边放水的事情是很多的：一边用手机一边充电、家庭的收支、水库放水和来水、牛吃草等，可见具体化让数学学习的作用更加鲜明，正如牛顿所说“一个例子胜过十个定理。”引导儿童多尝试举例、学会举例，只有从数学内部向外生长出数学事实，才能增强数学与生活的联系，提高儿童的数学学习能力。

3. 节外生枝放大化

对儿童而言，能把数学与生活自觉联系起来，或发现生活现象背后的数学实质，是一件比较困难的事情。因此当儿童有好的问题或好的发现时，一定要及时抓住，放大这些“节”外生出来的“枝”，并通过研究让这些“枝”茁壮成长、开花结果。如一儿童发现学校门口的时钟（二进制时钟）是坏的，每次就出现几个小点点时，引导他们对“钟坏了吗”进行研究，从而使他们不仅认识了二进制时钟，而且还了解了二进制、二维码等。再如儿童提出了“身高和体重能比吗”，放大这个问题，深入研究下去就拓展了对比的深层认识。“A4纸为什么叫A4纸”，深入研究就能发现其规格之间的联系、比例、由来等。这样每一次研究都成了“火种”，都会点燃儿童发现更多“枝”的热情，从而让他们品到数学与生活对接后的芳香。

三、温度，关注有效情感“增”

情感总是伴随学习的全过程。“感人心者，莫先乎情。”在数学课堂上老师、数学、儿童之间的情感无时无刻地进行着相互传递、相互感染，亲师爱数向学，师亲数趣爱学，师学爱数成学。因此关注儿童数学学习中丰富的情感体验，让酸甜苦辣入好菜，让苦乐忧困成营养。关注这些积极的情感体验，帮助儿童对集真善美于一身的数学形成正确的认识与敬畏，激起他们的求真之意，向善之情，爱美之心，从而让课堂的温度因教师而更温暖，因数学而更有趣，因学生而更灵动。

1. 亲师信道儿童化

亲其师信其道。儿童有着天然的向师性，但要让数学学习“道法自然”，还要如卢梭所说“把儿童看作儿童”，基于这样的立场，努力去读懂儿童。“懂”儿童要像李吉林老师那样把自己当作长大了的“儿童”，要像华应龙老师“在课堂上我是学生”那样把自己教成学生。这样当把“师”“道”儿童化了，拉近距离，才会有师生间彼此共情共振，相互欣赏，温暖前行。

2. 增趣生情故事化

现在的教材一般是按照“情境—探究—应用”的体例进行编排的。教学中经常发现情境最先出场，最先离场，不知觉间成了过场，而且长期的情境固化也造成儿童的审美疲劳。因此教学中通过情境故事化，以讲故事丰富情境的内容，激发儿童学习的兴趣。而且讲故事也可应用到整个学习活动中，如柏拉图所说：谁会讲故事谁就拥有了世界。讲好故事、会讲故事，故事就能不断地激发起儿童的向学之情。如大头儿子和小头爸爸分蛋糕学习分数加减法、猪八戒吃西瓜学习分数大小比较、猪八戒分桃子学习商不变规律、围羊圈认识面积和周长的关系等，经典故事不断上演，让数学学习变得更有情趣。

3. 穷理尽性生命化

“尽数之理，尽人之性”，才能实现数学教学滋润生命的最终目标。尽数理让数有“生命”，循理问数，做人道理亦联通。尽人性尊重生命有温情，好奇敢尝试，发现有掌声，错误能包容，课堂上思想自由、思维绽放、情感交融，求真向善，成长在其中。如“搭配中的学问”教学时顺儿童之天性、循数学之原理展开了以下的活动：首先是出示学校食堂师傅精心设计的菜单，观察得出每天都是一荤一素搭配，而且一个月内不重复。接着提出问题并组织猜测：如果要一个月（20天）不重复，至少需要几荤几素？当然儿童猜对的很少。于是逼着他们想到需要从简单想起开始研究，从而把问题退到了一荤一素、一荤两素、两荤三素。当通过研究积累了经验后，再次组织猜测至少几荤几素时，错的非常少。验证后追问：为什么第一次猜对的少，第二次猜错的少？儿童的感悟就非常多了。最后是组织反思并学会感恩：要想20天不重复，其实很容易，但师傅们为什么没有这样做？我们对他们应该做什么？这样让数学载着“温度”育人，不仅让学生学会如何学数学，也学会了如何做人，在温暖的课堂中一起见证了生命的成长。

参考文献：

[1]  R. 柯朗，H. 羅宾. 什么是数学：对思想方法的基本研究[M]. 左平，张饴慈，译. 上海：复旦大学出版社，2012.作者简介：孙敬彬（1976-），本科学历，中学高级教师;先后曾获得江苏省特级教师，江苏省师德先进个人、江苏省小学数学教材实验先进个人、江苏省小学数学优秀青年教师、徐州市名教师、徐州市优秀教育工作者、徐州市基础教育先进个人等荣誉称号，是江苏省333高层次人才培养工程培养对象。现任教于北京市海淀区中关村第三小学，北京市特级教师。