深究，让探究指向数学核心素养培育

摘  要：“探索规律”是小学数学教材中不同于基础知识的一条内容线索，第二学段更是独立编排，不属于《义务教育数学课程标准》规定的必学和必考内容。其有趣的专题、问题解决式的编排、超越双基的弹性化要求，对于培养高层次数学核心素养具有独特价值。数学核心素养引领下的规律探索，不仅要探究，更要深究。让探究与精准分析、多维探析、深层剖析等有机整合，推动数学核心素养由问题解决走向数学思维把握乃至理性精神培育。

关键词：数学核心素养;深究

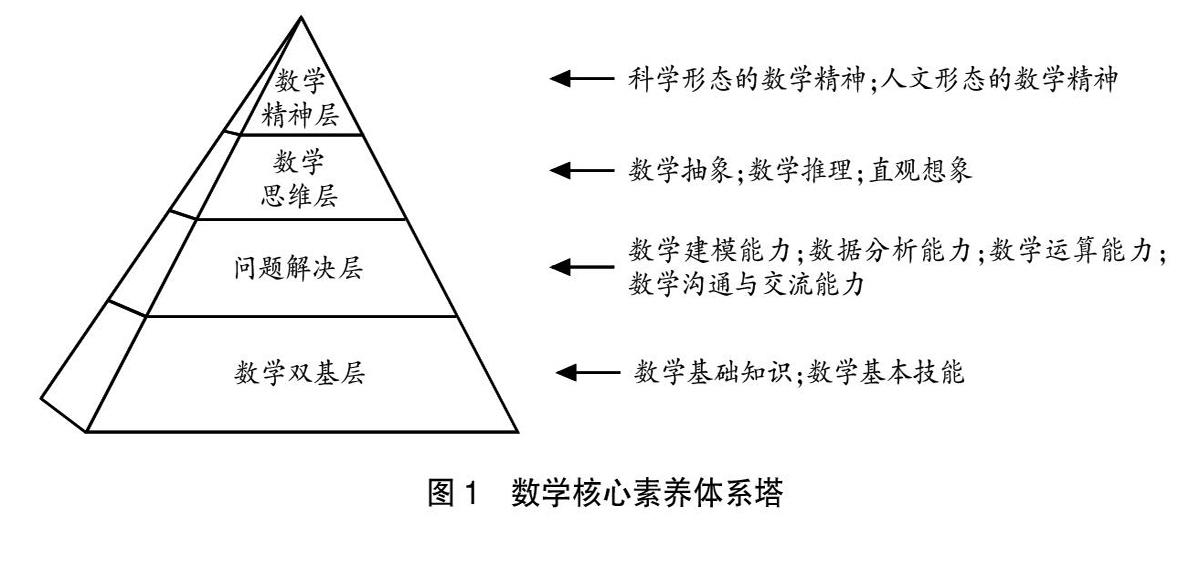
研究表明，数学核心素养体系可以划分为由低到高的四个层面：数学双基层、问题解决层、数学思维层、数学精神层。如图1。

“探索规律”是小学数学教材中不同于基础知识的一条内容线索，第二学段更是独立编排，不属于《义务教育数学课程标准》规定的必学和必考内容。其有趣的专题、问题解决式的编排、超越双基的弹性化要求，对于培养高层次数学核心素养具有独特价值。数学核心素养观照下的规律探索，不仅要探究，更要深究;不仅要动手，更要动脑;边探边思，探思结合，让规律探索不断指向高层次数学核心素养的培育。下面仅以苏教版四年级“多边形内角和”为例，谈谈具体的做法。

一、精准分析，涵养抽象眼光

情境1：探索四边形的内角和。

教师一般让学生依据三角形内角和以及从特殊到一般的思路，自主提出四边形内角和问题并展开探究。学生发现，四边形中最特殊的是长方形、正方形，它们的内角和都是360°，从而容易提出所有四边形的内角和可能都等于360°，进而从相对特殊的平行四边形和直角梯形等入手进行继续探究。然而交流展示时不难发现，学生想到的几乎都是“量”与“拼”，很少有学生能自主想到“分”。

“量”和“拼”本质上都是“做”，而“分”本质上是“看”，这种“看”实际是利用四边形与三角形之间的关系，由三角形内角和推理得到四边形的内角和。从“量”和“拼”拓展到“分”，并非只是方法数量的增加，更是涉及了方法视角的改变，即由感性的直观操作过渡到相对抽象的逻辑推理。学生之所以不能自主想到“分”，是因为学生无法自主建立起这样一种“抽象”的眼光。

研究表明，这种抽象一般要经历两个层次：对应和内涵。所谓对应，就是给这种方法起个名字;所谓内涵，就是要分析它的本质。在上述教学中要让学生戴上“分”这样一副抽象的“眼镜”，需要教师适时点拨：这些图形与已经学过的三角形有什么关系？你能用三角形的内角和推算出它们的内角和吗？更需要精准分析：这种“分”与过去所学的“量”和“拼”有什么不同？教学实践表明，适时点拨能让大多数学生能轻松想到用“分”的方法去求平行四边形和梯形的内角和，并以此为基础推算一般四边形的内角和;适时分析，能让大多数学生理解这里的“分”本质上是由动手实验转换到动脑推理，借助推理探求新知。一系列深究，使得抽象的眼光得以真正建立。

二、多维探析，引发高阶思维

情境2：探索五边形、六边形的内角和。

教师提供五边形、六边形材料，同桌两人运用“分”的方法，由三角形的内角和探究五边形、六边形的内角和。交流展示时可以发现，五边形相对容易，有的学生甚至还想到了把五边形分成一个四边形和一个三角形，但评讲时教师对该分法视而不见;六边形相对困难，不少学生无从下手。通过课后访谈笔者了解到，教师之所以对学生的“另类”分法持忽略态度，是源于其认为该分法所对应的算法与最后的一般算法不一致，它的呈现会干扰规律的探索与发现。

从四边形到五边形、六边形，随着边数增加，研究的对象变得越来越复杂，方法也变得越来越多元，对思维的要求也越来越高。澳大利亚学者比格斯曾提出SOLO思维结构分类理论，该理论认为，不论是儿童还是成人，高层次思维结构的形成一般要经历前结构、单一结构、多元结构、关联结构、抽象拓展结构等五个阶段。由此看来，学习四边形内角和时刚刚掌握的“分”法，只是将“前结构”提升为一种清晰的新结构，该结构还非常肤浅、简单，属于“单一结构”阶段，所以五边形的迁移相对容易，而六边形探究相对困难。

显然，在后续学习中，多元方向的探究有可能实现思维的突破。因而上述五边形的“另类”分法，其实是一种可贵的探索。虽然它可能意味着该学生尚未认识到分割最佳的结果（三角形），表征着一种低层次的转化，但它却呈现了难得的另一种可能。因此，教师应及时肯定该学生的想法和算法，进而展开深究：仔细观察其中的四边形，联系刚刚所学的四边形分法，你又有什么发现？引导学生感悟递推的美妙，理解分成三角形的奥妙，尝试将这些分法运用到六边形的探究中。

教学实践表明，单一结构一旦被突破，学生还能找到更多“分”法，如从一个顶点开始，由内部的一个点出发，抑或从某条边上的某一个点出发，等等。不过，高阶思维的建构还需要进一步深究：这些貌似不同的“分”法有没有相同的地方呢？不少学生能认识到，“分”法虽有所不同，但最终都可以分成若干个三角形，都恒等于若干个180°。这样，深究又让高层次的关联结构、抽象结构的把握成为现实。

三、深层剖析，激活直观想象

情境3：探索多边形内角和的一般规律。

教师让学生自己画出一些七边形或八边形，继续用“分”的方法探索它们的内角和，再按照图形名称、边数、分成的三角形个数、内角和等，把已有探究结果整理成表格，看看有什么发现。在教学现场可以看到，对学生来说，画出七边形、八边形等更为复杂的多边形似乎是一个不小的挑战，列表整理也多是一种耳提面命式的操作。

多边形有凸多边形和凹多边形，小学阶段没有特别说明，就默认为凸多边形范畴。笔者曾尝试画出七边形、八边形等，发现一不小心就画成了凹着的七边形和八边形，这里让学生画多边形，可能会让他们遭遇到凹多边形的情形，从而超越最近发展区。

不过，这种探究并非没有价值，关键要使之成为提升思维水平的一个契机，而这一目标的达成还是离不开深究。不妨在学生动手探究遇到困难时，适时提问：随着边数的增加，多边形变得越来越复杂，“分”还是一种很好的方法吗？从而让学生感受到“分”法的局限性;进而追问：动手操作已经不能很好地解决问题了，能不能动动脑筋找找其中是否蕴藏着什么规律呢？从而让列表整理成为模型思想引领下的探究，而非盲目的数学运作。

相关规律的解释，如多边形内角和为什么总与三角形内角和有关？分成的三角形的个数为什么总比多边形的边数少2？可以引导学生由简单图形激活对复杂多边形的直观想象，借助想象剖析：因为多边形都可以分成若干个三角形，而分成的三角形中，总有两个三角形中的两条边是多边形的边，而其余的三角形，都只有一条边是多边形的边，所以三角形的个数总比多边形的边数少2，从而实现对算法模型及其要素关系的通透理解。

对照数学核心素养体系塔的更高目标，不难发现，多边形内角和的探究，還需要更为深入的反思：其方法从“量”与“拼”到“分”，再从“分”优化为“算”，这些变化是否仅仅出于简便的考虑？对于某一个多边形来说，如果“量”的结果与“算”的结果不一致，是不是一定意味着“算”错了？让学生感悟这个规律并非动手测量的直接结果，而是人类理性思维绽放的花朵，进而让学生数学核心素养的培育由数学思维的把握走向更高层次的数学精神的领悟。

总之，数学核心素养引领下“探索规律”的教学，需要教师把一系列连贯的规律探究活动合理地划分为若干个环节，让探究适时与深究整合，引导学生由问题解决层走向数学思维层，训练抽象、推理、想象等数学思维方式;让深究适时与反思结合，引导学生由数学思维层进一步走向数学精神层，洞悉数学独特的理性和人文精神。

基金项目：此文系江苏省教育科学“十二五”规划（2015年度）课题“小学数学教学领域操作要义的创新研究”（编号：D/2015/02/285）成果之一。

作者简介：朱洁芬（1966-），本科学历，教育硕士学位，中小学高级教师，从事小学数学教学。