铰接式空间桁架结构模态试验研究

王桂伦， 姜 东， 周李真辉， 费庆国

(1. 东南大学 空天机械动力学研究所，南京 211189； 2. 东南大学 工程力学系，南京 210096；3. 南京林业大学 机械电子工程学院，南京 210037)

随着航天科技的发展，航天结构趋于大型化、柔性化和高精度化。空间可展结构以其展开精度高、质量轻、强度高等优点在航天领域的应用越来越广泛[1-2]。铰接式桁架结构是空间可展开结构中研究最早、应用最为广泛的一维空间展开机构，主要用于高精度探测设备定位和支撑[3]。铰接式桁架的动态特性直接影响其展开精度和探测设备的工作状态，因此有必要对桁架结构的动力学特性和相关试验技术进行研究，为桁架结构地面模态试验获得准确的模态参数提供支持。

目前，新型可展结构设计方面已经取得较大进展。Zhang等[4]采用具有形状记忆的聚合物复合材料制作了一种新型可展桁架结构；Li等[5]设计了两种基于形状记忆聚合物复合材料的可展桁架结构；Qi等[6]采用Bricard连接装置制作了大型支撑臂、可展平面桁架和环形桁架。

由于运载技术的限制和大折展比的要求，可展结构中含有大量的铰链。Tan等[7-10]通过动力学试验分析了铰链非线性对桁架结构的动力学特性的影响。Folkman等[11]和Bingham等[12]分别研究了含铰链桁架结构的阻尼特性以及重力对铰链阻尼的影响。陈鹿民等[13-15]研究了铰链间隙对结构振动频率、模态和阻尼等动态特性的影响。

可展结构的工作环境为微重力环境，在地面对结构进行模态试验时无法完全消除重力的影响。悬挂法具有结构简单、成本低等优点，故常用来模拟结构在地面模态试验中所需的自由-自由边界条件。Moon等[16]采用橡胶绳悬挂的方式抵消了可展桁架结构的重力，通过锤击法研究了含铰链可展桁架的动力学特性。关富玲等[17]对2 m天线试验样机采取悬挂法消除重力影响并进行了振动测试试验。曹长明等[18]通过振动台试验和锤击法试验获得了星载预应力可展开结构的模态参数。由于可展结构柔性大，当采用悬挂消除结构重力时，悬挂条件对试验结果影响往往不能忽略，同时铰链的存在导致结构模态试验的可重复性较差。

针对铰接式桁架结构的特点，采用悬挂方式抵消结构重力，对桁架结构开展模态试验研究，得到了桁架结构的固有频率、振型和阻尼比等模态参数。研究了悬挂刚度、悬挂点数、拾振点位置、悬挂长度对模态试验结果的影响。为之后大尺寸柔性可展桁架结构的试验模态分析提供参考。

1 铰接式空间桁架结构

铰接式空间桁架结构是典型的空间可展结构，由基本桁架单元铰接而成。桁架单元由横杆、竖杆、球铰、角块、拉索和锁定装置等构件组成，如图1所示。四根横杆通过四个角块互相连接构成刚性平面框，四根竖杆两端分别与上、下两个刚性平面上的角块通过球铰铰接构成一个桁架单元。上、下刚性平面框可以相对桁架单元轴线转动实现桁架单元的展开和收拢。

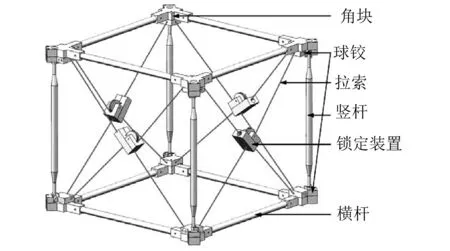
图1 桁架单元的组成

为了便于分析铰链对可展桁架锁定后模态试验的影响，省略拉索和锁定装置。将桁架单元上部的4个角节点作镜像处理，使得上下两个刚性平面框无法相对转动，从而实现桁架单元的自锁。简化后的桁架单元和角点如图2所示。不同数量的桁架单元铰接在一起构成不同长度的桁架结构。本文试验所采用的两种桁架结构分别由12个和22个桁架单元相互铰接而成。其中，12框桁架结构总长为3.6 m，质量为13.8 kg；22框桁架结构总长为6.6 m，质量为24.6 kg。桁架结构基本参数如表1所示。

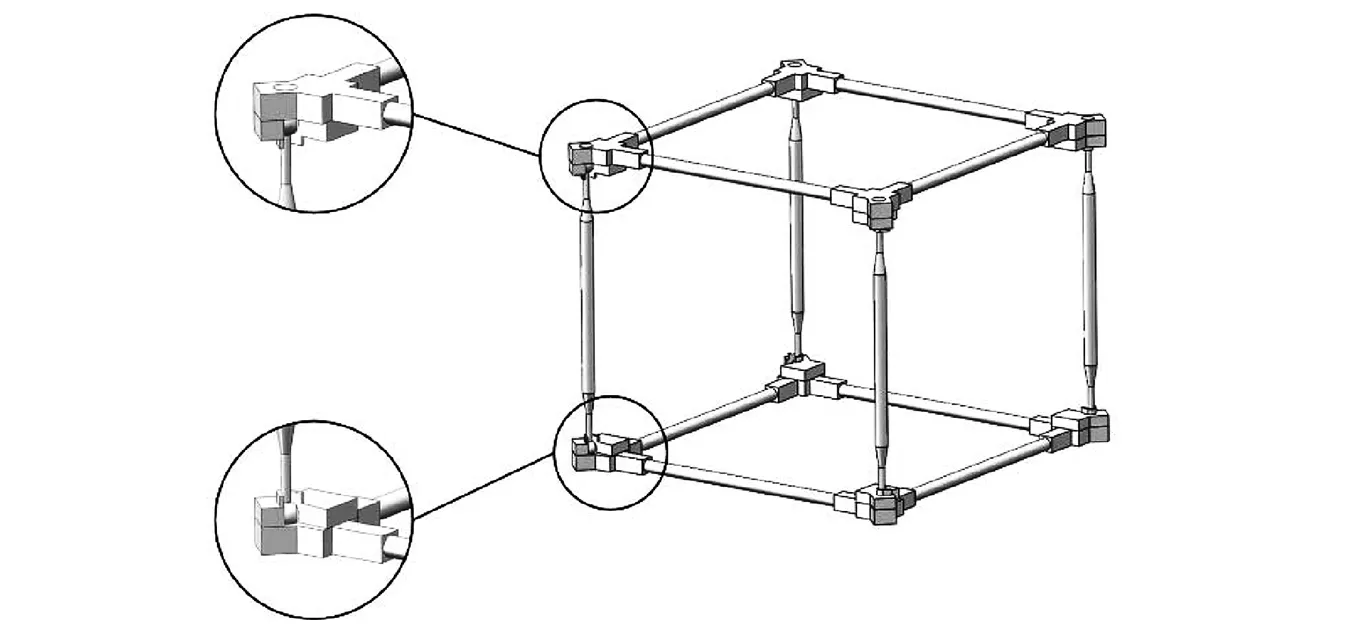
图2 简化后的桁架单元及角点

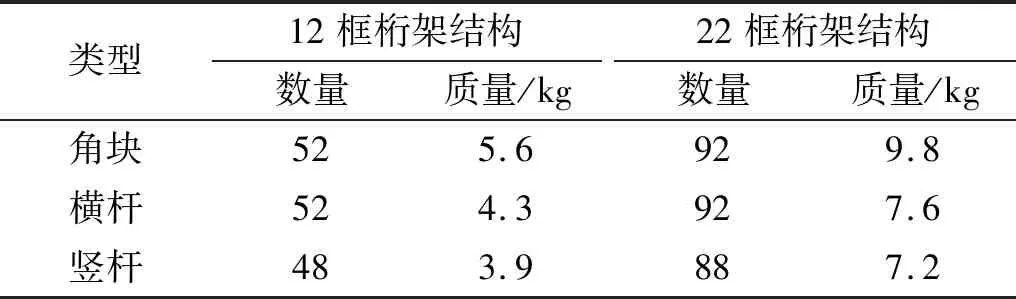
类型12框桁架结构数量质量/kg22框桁架结构数量质量/kg角块525.6929.8横杆524.3927.6竖杆483.9887.2

2 桁架结构模态试验

2.1 试验系统

本次模态试验采用型号为CA-YD-107的压电式加速度传感器，其质量为28 g，电荷灵敏度为6.05 pC/ms-2，使用频率为0.5～5 kHz。采用型号为CL-YD-303的力锤，其参考灵敏度为3.99 pC/N。分析仪器采用南京安正软件工程有限公司开发的振动及动态信号采集分析系统CRAS V7.0，模态分析软件采用MaCras。试验系统，如图3所示。

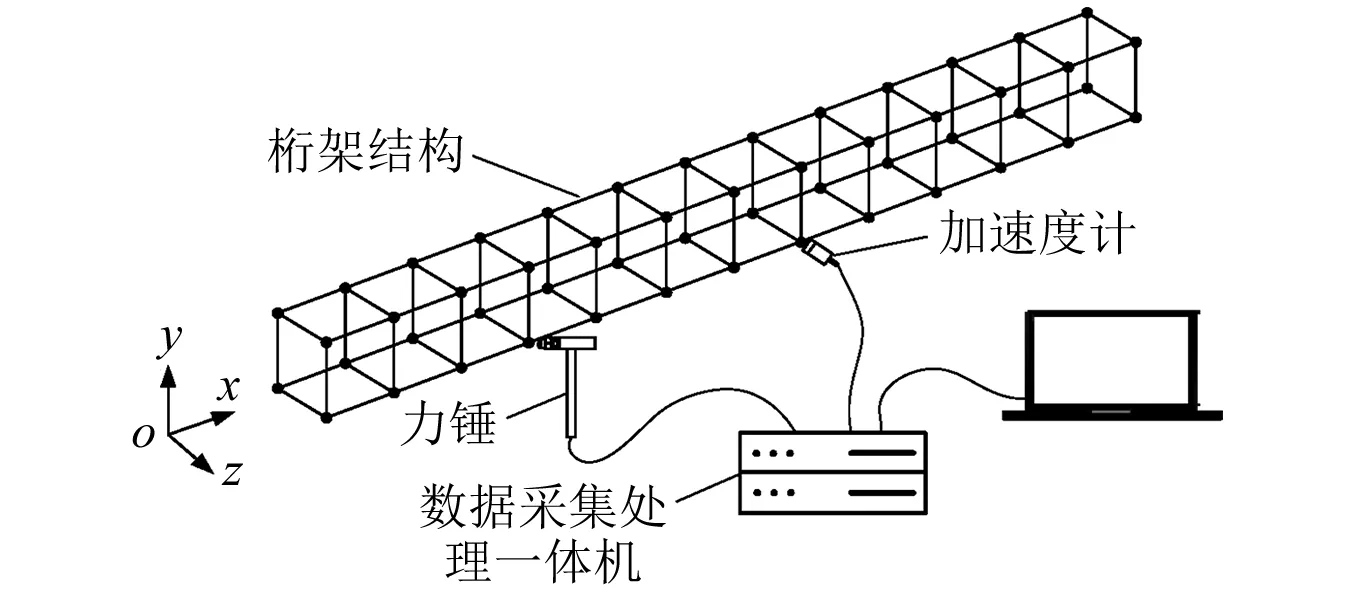
图3 试验系统

2.2 试验方案

试验采用单点拾振的测试方法，以加速度响应点为参考点，力锤激振遍历各个激励点。试验采用弹簧悬挂模拟测试所需的自由-自由边界条件。为尽可能完整地获取模态信息和辨识振型，将桁架每个角块节点选为激励点，激励点分布及其编号，如图4所示。

图4 12框桁架激励点分布及编号

通过数据采集处理一体机采集处理力信号和加速度信号，利用MaCras进行参数识别，得到结构的固有频率、振型和阻尼比等模态参数。

悬挂布置采用了如图5中(a)、(b)和(c)所示的三种方式。为了分析悬挂刚度、拾振点位置、悬挂点数对模态试验的影响，对12框桁架结构进行了七种工况的模态试验，各工况的具体说明如表2所示。对22框桁架结构进行模态试验，分析了橡胶绳悬挂长度对试验结果的影响。工况II采用橡胶绳悬挂桁架，其余工况采用弹簧。其中，弹簧刚度为105 N/m，橡胶绳刚度为25 N/m。工况I与工况II对比说明悬挂刚度对试验结果的影响，工况I与工况III、IV与VII对比说明响应点位置对结果的影响，工况I与工况V、VI对比说明悬挂点数对结果的影响。表2中拾振点和悬挂点位置参考图4中激励点编号。

图5 悬挂布置方式

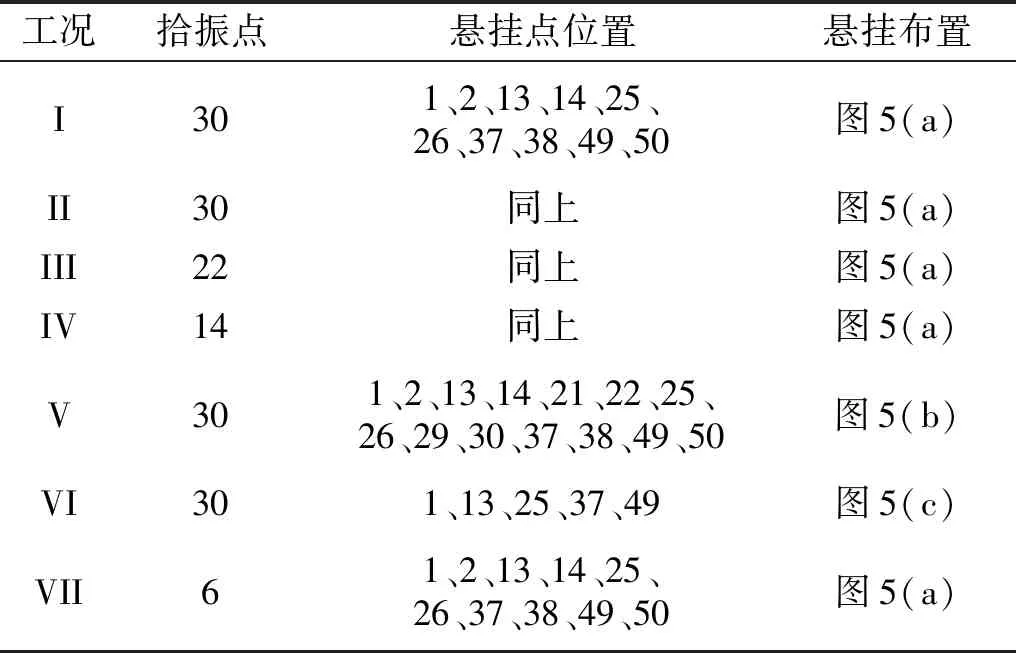
表2 各工况试验布置对比Tab.2 Comparison of different cases

3 桁架结构有限元仿真分析

利用MSC.Patran和Nastran软件对12框桁架结构进行有限元建模及模态分析，得到其固有频率和振型。在进行有限元建模时，采用梁单元模拟竖杆、横杆和角块，采用Bush单元模拟球铰。首先，建立球铰的精细化有限元模型，通过接触分析得到球铰等效线性刚度初值；其次，对3框桁架结构进行模态试验，得到结构的固有频率和振型等模态参数；最后，利用动力学模型修正方法识别出球铰的连接刚度，确定Bush单元中的六个刚度值。横杆和竖杆直径为11 mm，材料为铝合金，其弹性模量为68.9 GPa，泊松比为0.3，密度为2.7 g/cm3。12框桁架结构有限元模型，如图6所示。

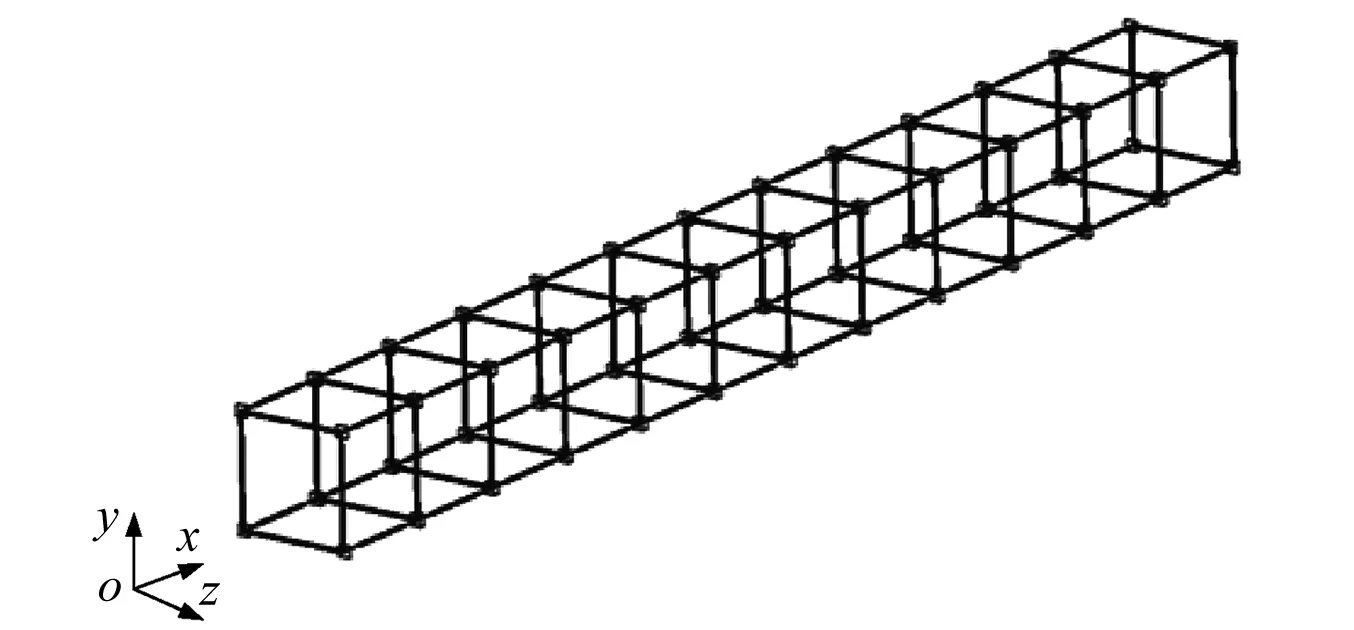
图6 12框桁架结构有限元模型

通过Nastran分析得到了自由边界条件下的12框桁架结构的前8阶固有频率和振型，为了便于与试验对比，仅提取出了xz平面内的振型图，如图7所示。

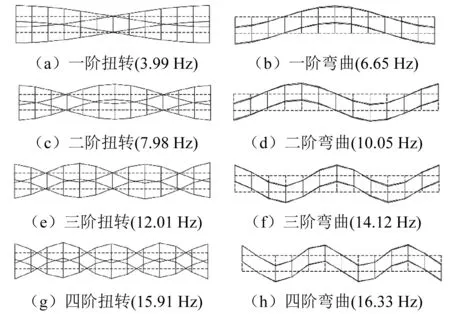
图7 桁架结构前8阶仿真模态振型与频率

4 试验结果分析

各个工况所识别的12框桁架结构固有频率如表3所示，可知试验所辨识出的桁架结构固有频率在20 Hz以内。

通过模态置信判定准则对这七个工况的模态试验结果的进行可靠性分析，验证了试验结果的合理性。工况II识别出的振型最多，故以工况II为例将其MAC值列于表4。表4对角线上的数值为各阶模态的相关系数，全部为100%；非对角线上的元素表示各阶模态之间的相关系数值。工况II的非对角线相关系数最大值为8.26%，说明各模态间的相关系数均较小，证明试验较好地激起了桁架结构的低阶模态，模态置信度较高。

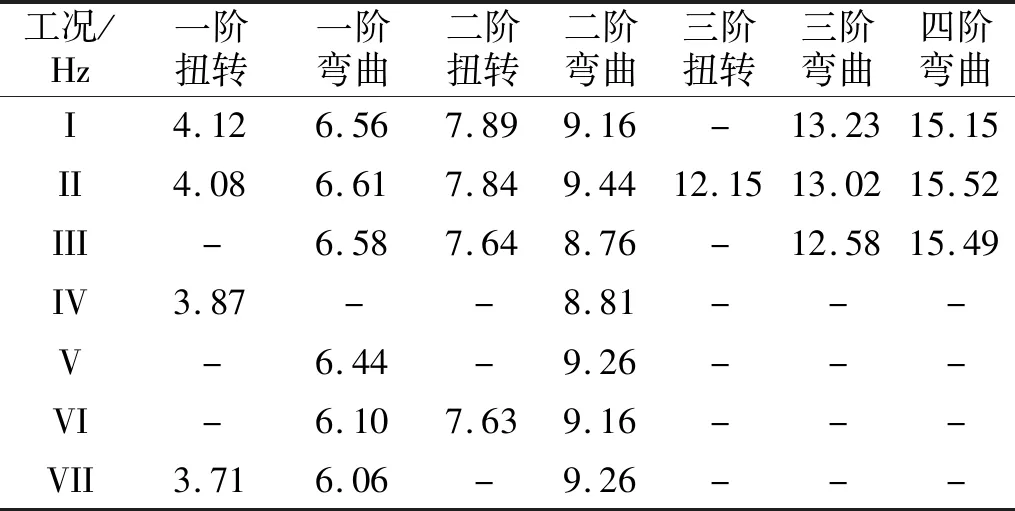
表3 各工况模态频率Tab.3 Natural frequencies of different cases

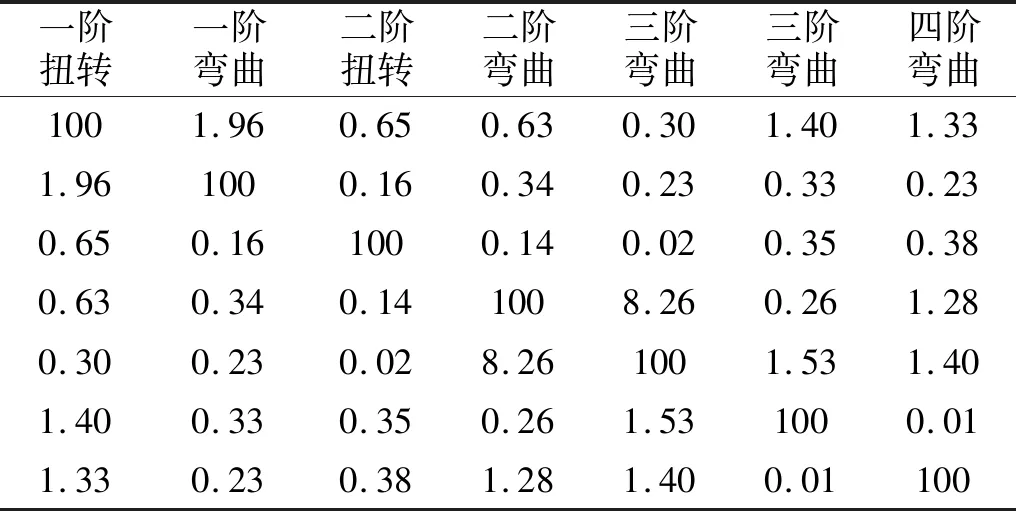
表4 工况IIMAC值矩阵Tab.4 MAC matrix of CaseII

4.1 悬挂刚度

工况I和工况II的加速度频响曲线如图8所示，其中第一阶共振峰为结构由悬挂效应引起的刚体模态。

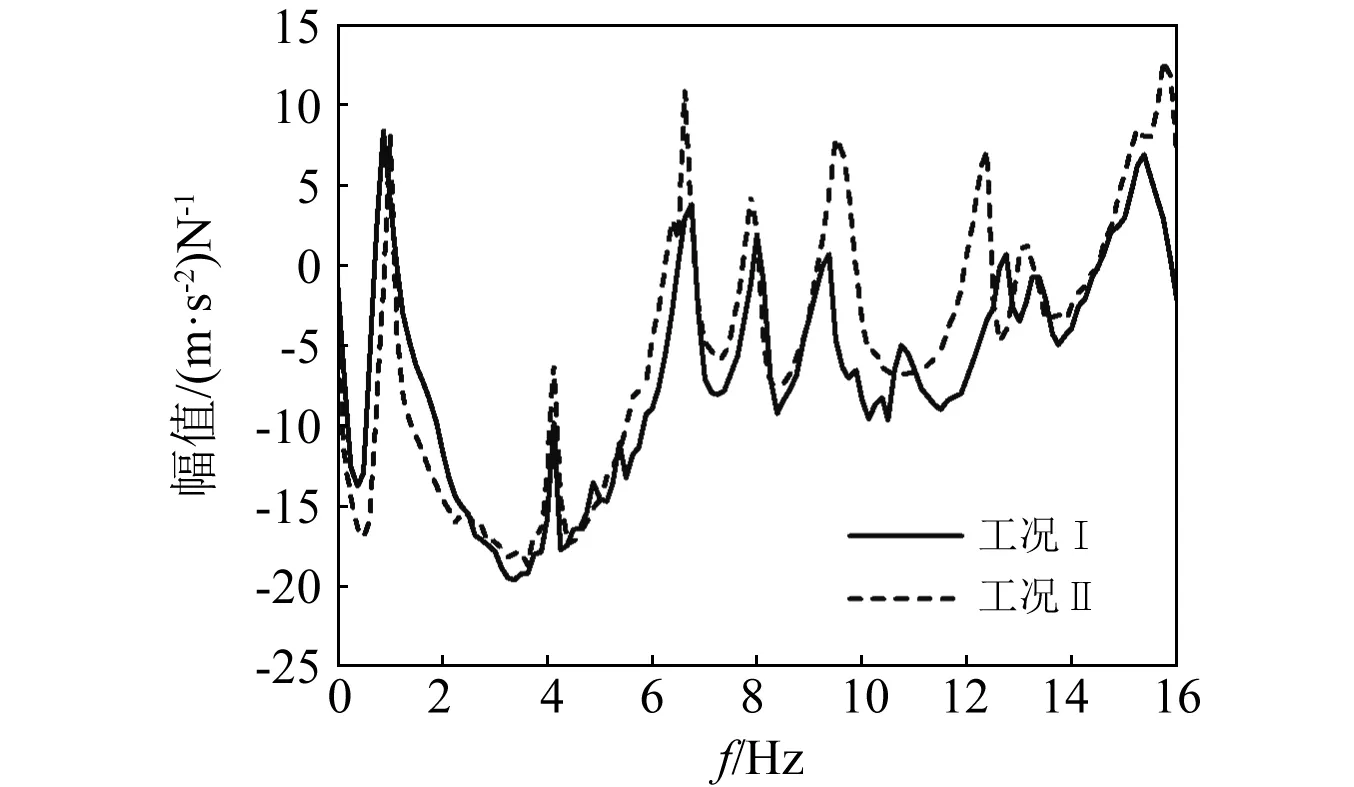
图8 工况I与工况II频响曲线对比

工况I和工况II的模态频率与仿真对比如表5所示，阻尼比对比如表6所示。工况II比工况I多识别出了第三阶扭转模态振型，且通过仿真分析得到了验证；此外，工况II的各阶阻尼比均小于工况I，因此工况Ⅱ试验结果较好。工况I未辨识出第三阶扭转模态，但辨识出了频率分别为10.74 Hz、12.51 Hz的两阶弯扭耦合模态。工况I出现弯扭耦合模态，一部分原因是桁架结构含有大量铰链，结构柔性大，模态密集；另一部分原因是由弹簧悬挂引入的附加阻尼较大，相邻模态混叠。试验结果表明：采用柔性大的橡胶绳能够降低悬挂附加刚度和阻尼比，有助于避免模态耦合，提高辨识结果的可靠性。

表5 工况I与II试验结果与仿真结果对比Tab.5 Comparison of simulation results and experimental results of Case I and Case II

表6 工况I与II阻尼比对比Tab.6 Comparison of damping ratio between Case I and II

4.2 拾振点位置

工况I、III、IV与VII试验结果与仿真对比，如表7所示。

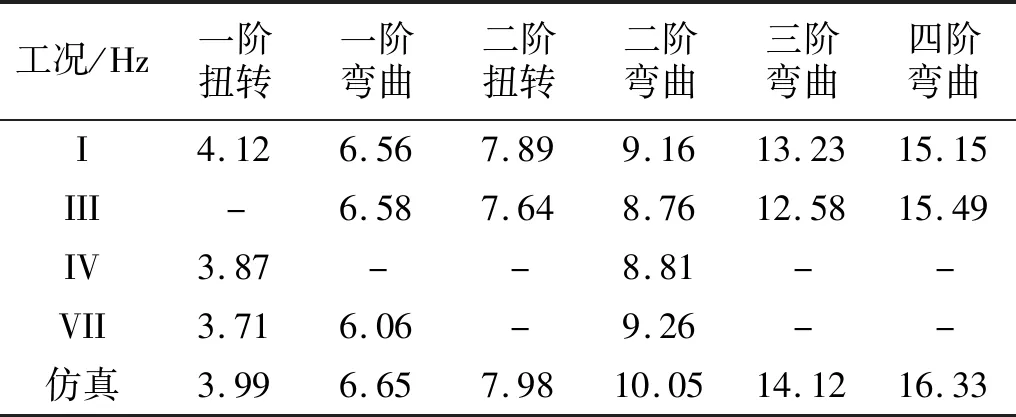
表7 工况I、III、IV和VII试验结果与仿真结果对比Tab.7 Comparison of finite element results and experimental results between case I、III、IV and VII

从表7可知，工况I和工况III辨识出的模态振型较多，试验结果相对较好。工况IV辨识出的模态振型较少是因为其拾振点是悬挂点同时又是振型节点。工况VII的拾振点靠近结构端部，而结构中的球铰间隙导致激励信号经过球铰时产生能量耗散，结构难以完全激振起来，导致模态振型丢失。当采用锤击法对含有大量铰链的结构进行模态试验时，拾振点应居中布置，同时避开悬挂点与振型节点，有利于减少激励传递的损耗，提高模态试验辨识结果的完备性。

4.3 悬挂点数

工况V在工况I悬挂的基础上增加了4个悬挂点，而工况VI仅采用5个悬挂点。工况I与V、VI试验结果与仿真对比，如表8所示。

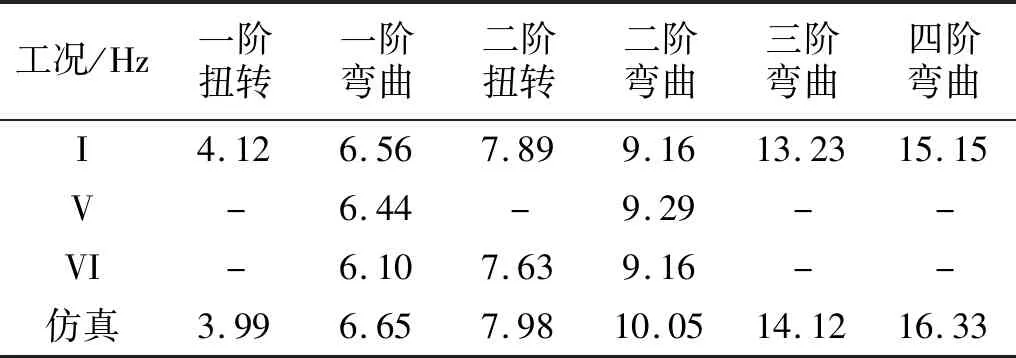
表8 工况I、V和VI试验结果与仿真结果对比Tab.8 Comparison of finite element results and experimental results between CaseI、V and VI

工况V增加了弹簧数量，桁架结构引入较大的附加刚度和阻尼，导致工况V仅辨识出低阶弯曲模态，而且出现了四阶弯扭耦合模态。工况V的悬挂集中，桁架结构中部产生挠曲变形，削弱了结构整体刚度和铰链连接刚度，导致工况V辨识结果相对较差。

工况VI的弯曲频率与仿真结果的误差较大。在工况VI的试验中，力锤敲击方向与弹簧悬挂方向不垂直，导致弹簧在激励方向产生约束，削弱力锤激励。此外，工况VI仅采用5个悬挂点，每个悬挂点处的受力较大，铰链发生滑移，间隙增大，采用锤击法难以将高阶模态激振出来。

当采用弹簧悬挂来模拟桁架结构自由-自由边界条件时，悬挂点应均匀对称布置，降低铰链对试验结果的影响，提高试验的可重复性。

4.4 悬挂长度

对22框桁架结构进行模态试验研究橡胶绳悬挂长度对试验结果的影响。由于悬架高度的限制，仅对比了两种悬挂长度下的模态试验结果。试验一和试验二的悬挂布置分别如图9和10所示，其中图9橡胶绳的长度为30 cm，图10橡胶绳长度为50 cm。

图9 试验一悬挂方式

图10 试验二悬挂方式

整个桁架结构共布置24个悬挂点和48个测点。悬挂点均匀对称布置，加速度计居中布置。试验结果与仿真结果对比,如表9所示。

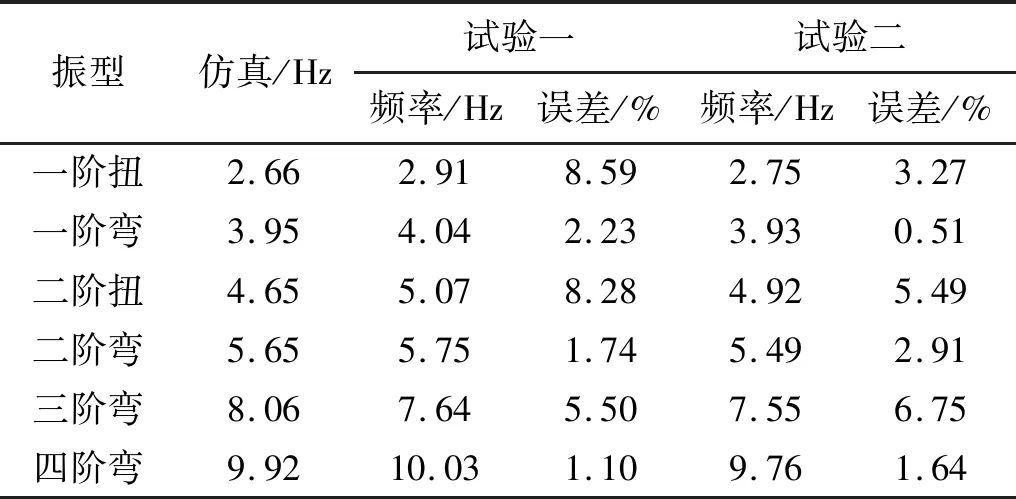
表9 试验一、二结果与仿真结果对比Tab.9 Comparison of simulation results and experimental results of Testone and two

从表9中可知，试验一和试验二仅辨识出了六阶模态频率和振型，且试验二的模态频率均低于试验一相对应的模态频率。增加橡胶绳悬挂长度，降低由悬挂单摆效应引起的刚体模态频率，减轻刚体模态对弹性模态的影响，提高了试验二试验结果的可靠性。

5 结 论

采用悬挂法抵消桁架结构的重力进而对其进行试验模态分析。针对桁架结构地面模态试验重复性差的特点，研究了悬挂刚度、拾振点位置、悬挂点数以及悬挂长度对模态试验的影响，为大型柔性可展结构的地面模态试验提供参考。主要结论为：降低悬挂刚度有利于避免耦合模态；拾振点居中布置可提高试验模态的完备性；悬挂点均匀对称布置，减轻铰链对桁架结构整体刚度的削弱，提高试验的可重复性；增加悬挂长度，可降低由悬挂效应引起的刚体模态对弹性模态的影响。