非饱和土地基振动响应分析
2019-07-08李伟华王文强
李伟华, 王文强
(1.北京交通大学 土木建筑工程学院,100044;2. GeoApplication Engineers Pte Ltd, 367903, Singapore)
动荷载下地基振动响应与波动规律作为土动力学基本问题之一,很早就被学者关注[1]。近年来随着我国高速铁路的发展,为这一问题的研究注入了新的活力,并促使其发展和完善。最初关于地基振动响应问题的研究是在单相弹性半空间中展开,并取得了相当丰硕的成果。自从Biot[2]建立了饱和多孔介质的波动方程后饱和土地基的动力问题研究得到了长足的发展。Philippacopoulos[3]、Rajapakse[4]、陈龙珠[5]、金波[6]、陈胜立[7]等就此发表了一系列论文,逐步完善了地基与基础的动力相互作用问题。然而实际上地球表面的土体大多数处于非饱和状态,通常我们所说的饱和土,实际上会或多或少含有一些微量气泡,是一种准饱和土。已有的研究证明,即使微量气泡的存在也会对土中波的传播特性产生很大的影响[8],所以研究非饱和土地基的动力响应更具有实际意义。
非饱和土体的动力特征比饱和土体动力特征要复杂的多,现有研究多停留在非饱和多孔介质中波的传播特性上。Berryman[9],Santos[10],Lo[11],Tuncay[12],Vardoulakis[13],Wei[14]和Lu[15]等分别依据Biot理论、混合物理论或二者的结合各自建立了非饱和多孔介质的动力方程,确定非饱和多孔介质中存在着1种剪切波和3种压缩波(P1,P2和P3波),并研究了其传播特征。由于非饱和介质动力方程的复杂性,往往需要借助数值方法对方程进行了求解。Zhao等[16]采用交叉网格有限差分方法求解了Santos提出的非饱和多孔介质方程,并结合完美匹配层边界研究了非饱和多孔介质中的波动。Wei[17]和Ravichandran[18]根据Wei所建立方程,建立有限元方法并分析非饱和土坝的地震响应。Gatmiri[19]和Maghoul[20]在准静态条件下推导了非饱和多孔介质动力方程的边界积分表达式,并给出方程的2D和3D的时域、频域解。Moldovan等[21]采用Hybrid-Trefftz应力单元法求解了Wei所建立的方程。目前,关于非饱和土地基的动力响应问题的研究并不多见。徐明江[22]以三相多孔介质模型为基础建立非饱和土的动力控制方程,采用解析方法研究了非饱和土半空间在表面荷载作用下的稳态和瞬态动力响应,以及非饱和土地基上刚性和弹性圆板基础的垂直振动问题。
鉴于用解析法求解非饱和土地基的动力响应问题的诸多限制,只有在少数特定的边界条件下才能求得,本文建立了一种非饱和多孔介质动力分析显式有限元方法。首先在Wei所建立的非饱和多孔介质动力方程的基础上,将其中的土水特征曲线模型改为能够更好描述接近饱和时土体特征的van Genuchten模型,然后通过时空离散,建立该方程的显式有限元表达式。该方法采用解耦计算,无需求解联立方程组,能够有效节省内存空间和提高计算速度,在求解Biot饱和多孔介质波动方程中已经得到了很好的应用[23]。利用此方法与局部透射人工边界结合,编制计算程序,分别建立刚性和柔性条形基础作用下非饱和土地基模型,分析了在竖向均布脉冲荷载作用下,饱和度、孔隙率等因素对的非饱和土地基振动响应的影响。
1 非饱和土地基动力方程
Wei以多孔介质混合理论为基础,考虑动态相容条件建立非饱和多孔介质波动方程:

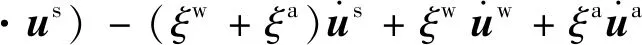
(1a)

(1b)

(1c)
式中:上角s,w和a分别代表非饱和土的固相、液相和气相。nα,ρα,uα(α=s,w,a)分别表示α相的体积分数、密度以及位移。rαα为弹性系数,文献[24]给出其与非饱和土各相的体积模量Kα、固体骨架的体积模量K、剪切模量G及有效应力系数αB的关系,
(2a)
(2b)
(2c)
(2d)
(2e)
(2f)
其中,
(3a)
(3b)
Θw和Θa是描述毛细管平衡条件的参数,对给定的饱和度Sr,有:
(4)
式中:pa-pw为基质吸力,对于给定饱和度,由土水特征曲线模型确定。Wei建立的非饱和多孔介质波动方程中,土水特征曲线及非饱和土的渗透系数均采用Brooks-Corey模型[25]。该模型存在导数不连续点,不能很好地描述土体接近饱和时的特征,而接近饱和时土水特征曲线形状上的微小变化都会导致预测水力传导率函数的显著变化,从而影响非饱和带水流模拟的结果,同时也会造成数值计算困难。为了更好地描述土体接近饱和时的特征,本文将其中的土水特征曲线及非饱和土的渗透系数改为van Genuchten提出的经验公式[26]。则基质吸力表示为,
(5)
式中:α,m,d为模型参数,且d=1-1/m,
(6)
式中:SrW为束缚饱和度;SrN为空气残余饱和度。
由线弹性状态下非饱和多孔介质的应力-应变关系,可以得到Θw和ΘN的关系,
(7)
联立式(4)~(7)即可求得Θw和Θa。
参数ξf(f=w,a)与渗透率k的关系如下,
(8)

(9)
2 显式有限元方程的建立
2.1 非饱和多孔介质动力方程的矩阵形式
定义如下矩阵:
(10)
(11)
(12)
利用上述矩阵表达,方程(1)可以表示为:
(13)
其中
2.2 有限元方程列式的建立
设N为单元形函数矩阵,则单元的位移向量uα,e和力向量fα,e可以分别表示为:
(14)

(15a)
(15b)
(15c)
式中:应变矩阵B=L·N。
2.3 离散方程及解耦方法
对于二维问题,采用4节点4边形等参单元,节点i和与其直接相邻的节点k构成局部节点系,此节点系中包含9个节点。根据式(13)可以直接得到如下离散公式:
(16a)
(16b)
(16c)
其中,
(17)
(18)
(19)
(20)
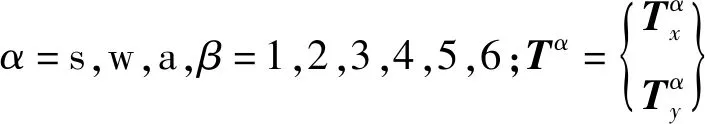
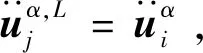
(21)
2. 4 节点动力反应的显式表达式
利用有限元方法建立离散的动力方程后,采用中心差分法与Newmark平均加速度近似格式[23]相结合的方法求解节点动力方程式(16)。得到由前一时刻的位移和速度表示的当前时刻位移的显式表达式,
(22a)
(22b)
(22c)
由前一时刻的位移和速度表示的当前时刻的节点速度反应的显式表达:
(23a)
(23b)
(23c)
由前一时刻的速度和此时刻的速度表示的加速度的显式表达式
(24)
式(22)~(24)为非饱和多孔介质局部节点系下某一节点的动力反应的显式表达式,该节点的动力反应只与相邻节点的动力反应有关,从而实现了方程的解耦求解。
2.5 动力人工边界
对半无限域地基进行有限元模拟,需要引入动力人工边界,本文采用局部透射边界[27],非饱和多孔介质中的4种波(P1,P2,P3,S波)都以其固有的波速向前传播。无论是固相、液相还是气相,对某一特定的波来说,都是以同一波速沿同一方向向前传播,且气相、液相位移与固相位移具有固定的关系。因此,可以假设非饱和多孔介质的固相、液相、气相位移分别以同一波速通过人工边界,针对固相、液相、气相分别应用多次透射人工边界。
3 有限元求解精度验证
鉴于目前关于非饱和多孔介质动力反应问题分析的解析解较少,且非饱和多孔介质动力反应的控制方程不统一,很难找到与本文中的控制方程符合的解析解,因而为了验证计算方法的可行性,本文采用了以下两种方法:方法一:将非饱和多孔介质动力控制方程退化为饱和多孔介质,与文献[28]的解析解进行对比验证。假设孔隙中只含有水,即非饱和多孔介质的饱和度为1(气相体积分数为0),将气相相关参数设为零,方程(1)可以退化到饱和状态:
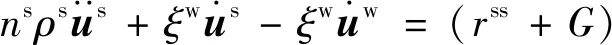
(25a)
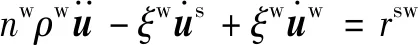
(25b)
式中的各项参数与Biot提出的饱和多孔介质动力方程的参数对比情况见表1。
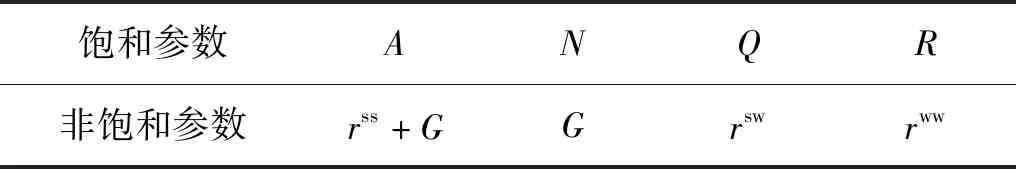
表1 参数对比
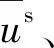

表2 饱和土材料参数
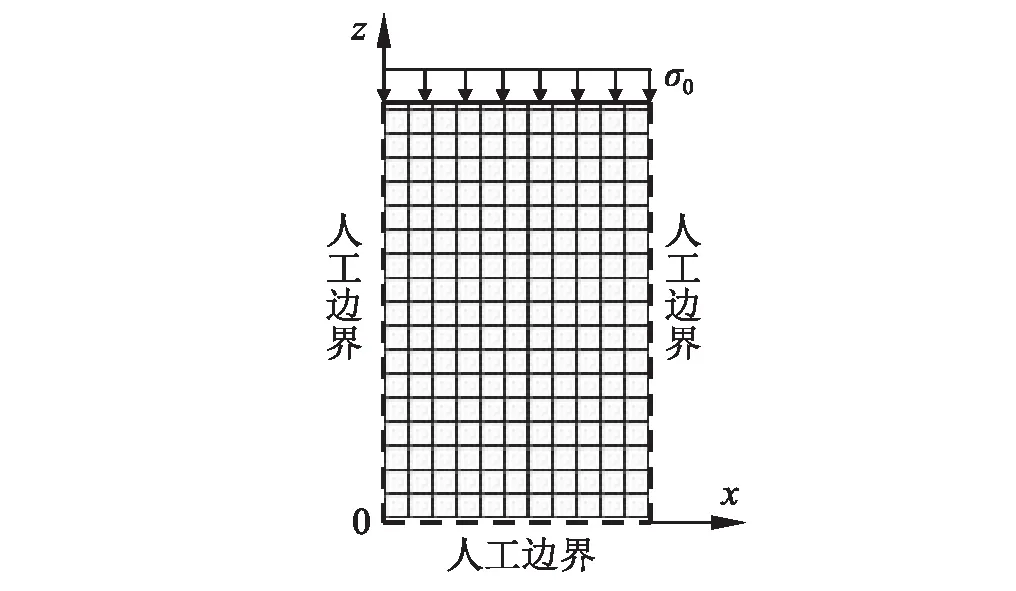
图1 验证模型及网格划分示意图
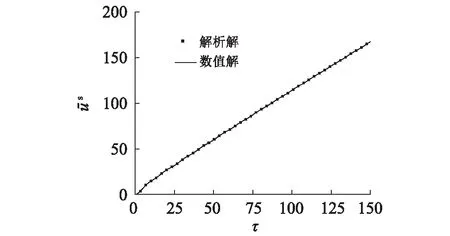
图2 验证一: 固相位移时程图
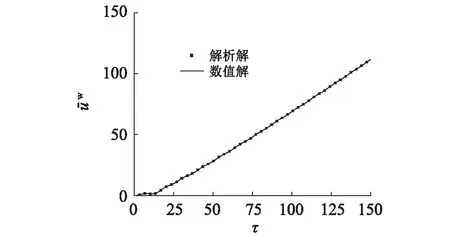
图3 验证一:液相位移时程
方法二:将气相用液相代换,且假设两种液体的材料参数相同,这样可以保证方程的完整性。采用和方法一相同的分析模型和参数,图4给出了孔隙被两种相同液体充满时,自由表面固相位移随时间的变化曲线。可以看出,第二种方法的计算结果与文献[28]的解析解十分接近,由于将单种液体划分为两种液体,计算过程中多考虑一个界面的影响,会使计算结果产生一定差别。但结果依旧能很好地反映出本文计算方法的可靠性。
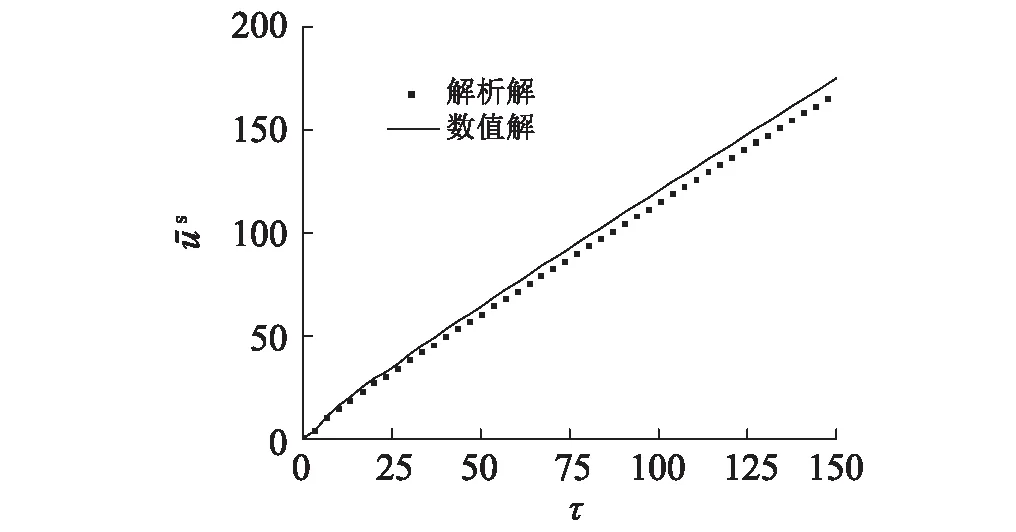
图4 验证二:固相位移时程图
4 非饱和土地基振动分析
4.1 地基模型及土层参数
在地基表面处有一宽为4 m(2b=4 m)的条形基础,基础底面作用幅值σ0=1 kPa作用时间T=0.5 s的竖向均布脉冲荷载。分别考虑刚性基础和柔性基础两种情况,不考虑地基与基础的相互作用及基础自重,将基础简化为竖向均布条形荷载作用在地基表面。计算模型如图5所示。取计算区域为40 m×30 m,网格尺寸为1 m×1 m,网格划分及坐标如图所示。地基土的物理性质见表3。在基础中心点A以下不同深度及地基表面距A点不同距离处取观察点,分析非饱和土地基振动规律及饱和度对非饱和土地基振动的影响。
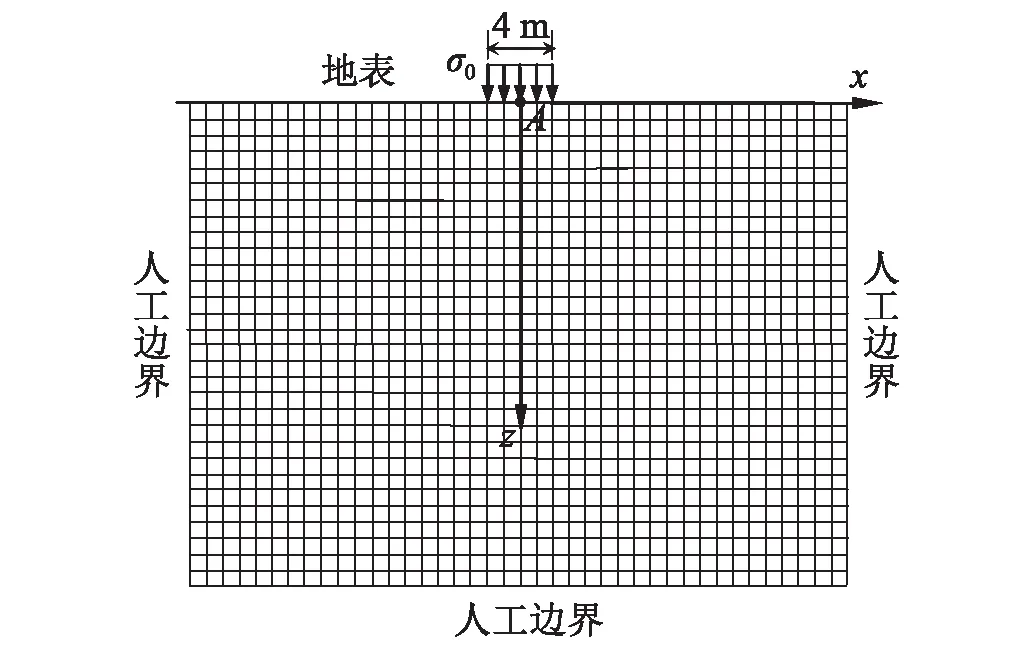
图5 地基计算模型图

K/PaG/Paρs/(kg·m-3)ρw/(kg·m-3)ρa/(kg·m-3)2.59×1071.94×107270010001.10Ks/PaKw/PaKa/Pavw/(Pa·s)va/(Pa·s)3.6×10102.0×1091.0×1051.0×10-31.5×10-5k/μm2αBαmn01.01.01.0×10-42.00.36或0.6
4.2 刚性基础作用下非饱和土地基动力反应分析
考虑非饱和土地基表面与基础接触面上各点满足以下条件:①刚性接触面上各点固相竖向位移相等;②刚性接触面内外均为透水边界。
图6给出了当土体的初始孔隙率n0=0.36时,基础中心点下各点的固相竖向位移幅值,其中图6(a)为各点竖向位移随饱和度变化的关系曲线;图6(b)为不同饱和度下基础中心点下竖向位移沿深度(z/b)变化曲线。
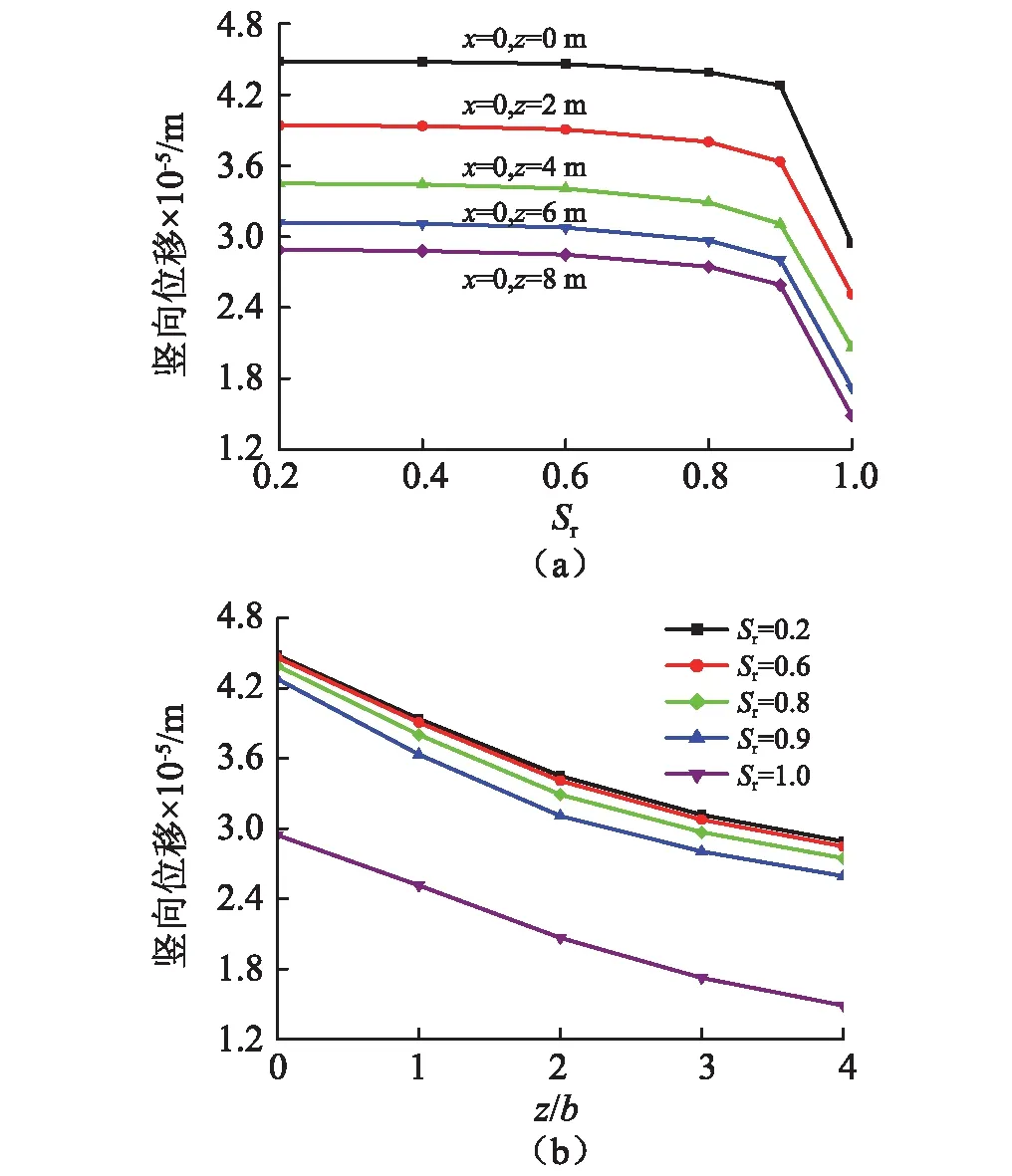
图6 刚性基础中心点下不同深度处各点竖向位移幅值(n0=0.36)
从图6中可以看出,当地基土不饱和(Sr<1)时,随着饱和度的增加,刚性基础中心点下各点竖向位移减小,且减小程度随着饱和度的增加变得明显。这主要是由于随着饱和度增加,土中基质吸力降低,有效压应力减小所致。而且当土体饱和度较小时,孔隙中含有较多的空气,孔隙流体的压缩性增加,由荷载引起的孔隙流体压力较小,饱和度变化对骨架位移影响不大。当地基土完全饱和(Sr=1)时,各点竖向位移较Sr<1时有显著降低。说明在土体接近完全饱和时,即使饱和度发生微小变化都会影响基础中心点下各点的竖向振动。这是因为当土体接近饱和时,土中气体以封闭气泡形式存在,气体含量的减小,会导致孔隙流体的体积模量显著增加,从而使得土体抵抗变形能力增加。从图中还可以看到,基础中心点下各点的位移沿深度方向衰减。靠近中心点处衰减较快,远离中心点各点位移随深度变化趋于平缓。
图7给出了当土体的初始孔隙率n0=0.36时,地表固相竖向位移幅值,其中图7(a)为地表各观察点竖向位移随饱和度变化的关系曲线;图7(b)为不同饱和度下地表竖向位移沿水平方向(x/b)变化曲线。
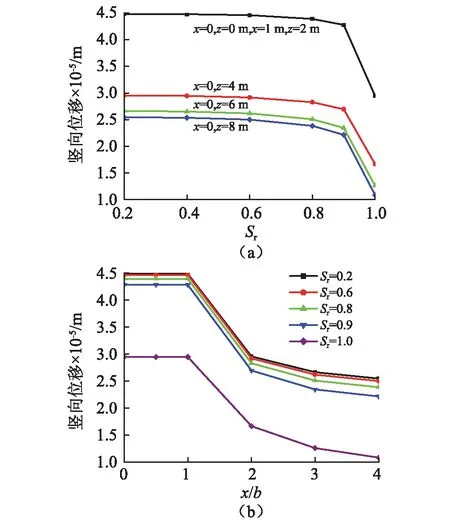
图7 刚性基础地基表面各观察点竖向位移幅值(n0=0.36)
从图7中可以看出,和基础中心点下竖向位移一样,随着地基土体饱和度的增加,地表各点竖向位移减小。当饱和度较小时,各点竖向位移随饱和度变化不大,饱和度较大时,饱和度对各点竖向位移的影响变得愈加明显。且当Sr=1时,各点竖向位移较Sr<1时有显著降低。从图中还可以看到,地表各观察点的竖向位移随观察点到荷载中心点距离的增加而减小。因为是刚性基础,荷载作用范围内各点位移相等,当1
图8给出了当土体的初始孔隙率n0=0.36时,地表固相水平位移幅值,其中图8(a)为地表各观察点水平位移随饱和度变化的关系曲线;图8(b)为不同饱和度下地表水平位移沿水平方向(x/b)变化曲线。图中负号表示水平位移与坐标方向相反。
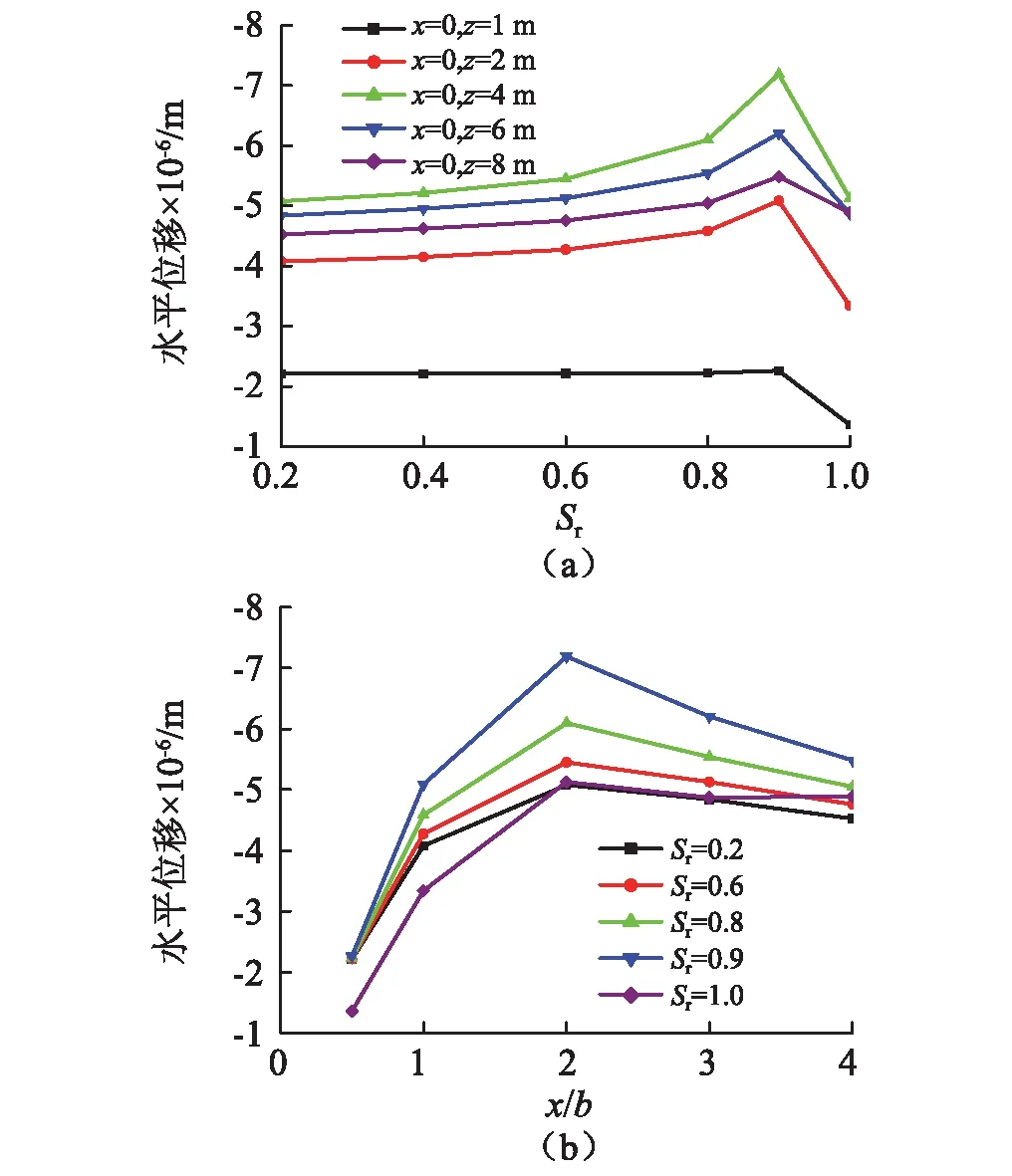
图8 刚性基础地基表面各观察点水平位移幅值(n0=0.36)
从图8中可以看出,当Sr<1时,随着饱和度的增加,地表各点水平位移大小增加,饱和度较小时,变化不大,饱和度较大时,增加明显。这主要是因为当Sr<1时,随着饱和度的增加,土体中的基质吸力降低,水平方向有效拉应力增加,导致水平方向产生的与坐标方向相反的位移大小增加。当Sr=1时,地表各点水平位移大小较Sr<1时反而降低。这是由于孔隙中封闭的气泡使得地基土体接近饱和时孔隙流体的体积模量较饱和时显著降低。从图中还可以看到,地表同一观察点的水平位移较竖向位移小近一个数量级,地表各观察点的水平位移随观察点到荷载中心点距离的增加先增加后减小,在x/b=2时达到最大值。
为了分析土体初始孔隙率不同时饱和度对地基振动的影响,图9~图11分别给出了当土体初始孔隙率n0=0.6,其他参数保持不变时,不同饱和度下,基础中心点下以及地表的固相竖向、水平位移幅值分布。从图中可以看出,n0=0.6时饱和度对各点振动响应的影响规律与n0=0.36时相同。当土体其他参数相同时,初始孔隙率大的,饱和度对各点振动响应的影响较大。当Sr<1时,初始孔隙率大,地基土体各点振动反应较初始孔隙率小时增加明显;当Sr=1时,初始孔隙率的大小对地基振动响应影响不大。再次说明非饱和土中气相状态的存在对地基振动响应的影响。
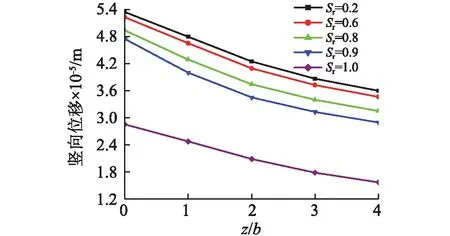
图9 刚性基础中心点下竖向位移幅值沿深度分布曲线(n0=0.6)
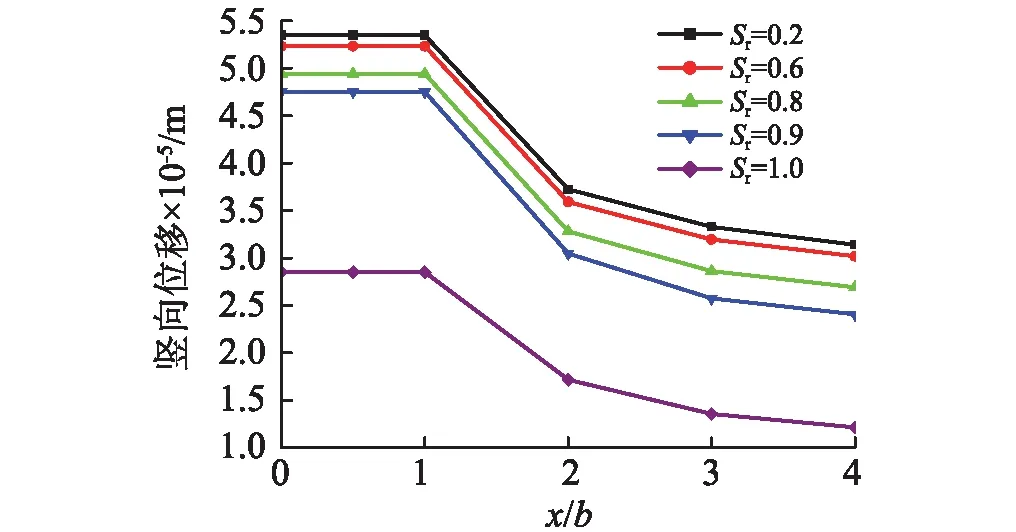
图10 刚性基础地基表面竖向位移沿水平方向分布曲线(n0=0.6)
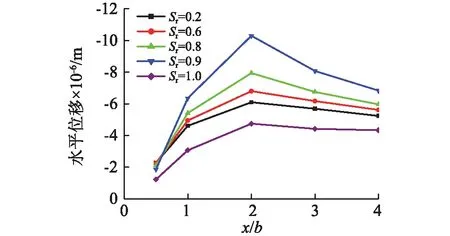
图11 刚性基础地基表面水平位移沿水平方向分布曲线(n0=0.6)
4.3 柔性基础作用下非饱和土地基动力反应分析
考虑非饱和多孔介质的自由面与柔性基础接触面上各点满足以下条件:① 柔性接触面上各点的位移不加以约束;②考虑柔性接触面间的滑动,在接触面内外皆为透水边界。
图12给出了不同饱和度下,土体初始孔隙率分别为0.36、0.6时,基础中心点下固相竖向位移幅值沿深度的分布。
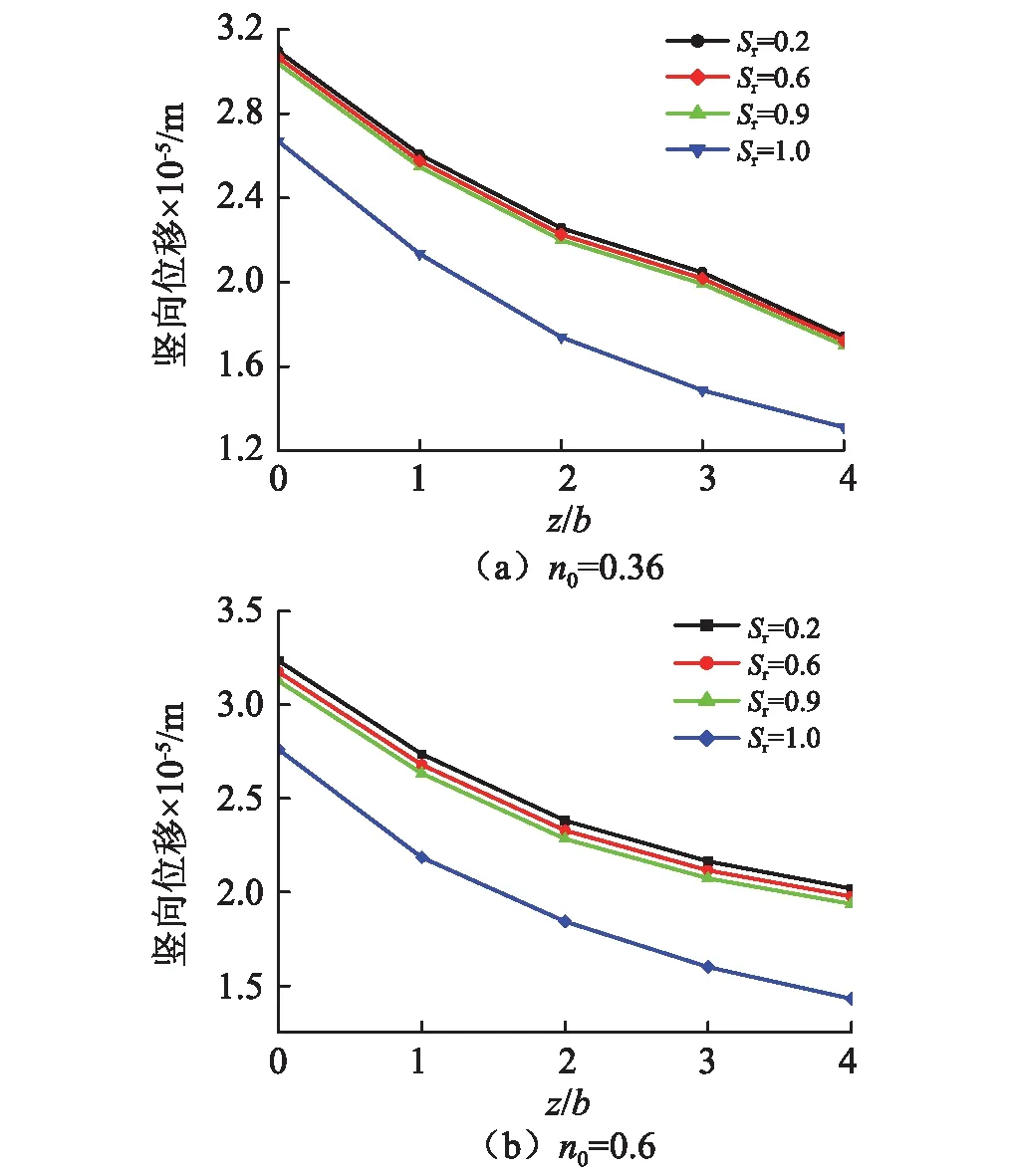
图12 柔性基础中心点下竖向位移幅值沿深度分布曲线
从图12中可以看出,与刚性基础相比,柔性基础条件下,基础中心点下相同位置处的竖向位移幅值要小。这与现有的研究结论,随着基础柔度增加,地基动力柔度系数增加是一致的[29]。在柔性基础条件下,当Sr<1时,饱和度的变化对基础中心点下竖向位移幅值影响不如刚性基础条件下明显,初始孔隙率较大时,饱和度对基础中心点下固相位移幅值影响稍有增加,随着饱和度增加基础中心点下固相位移幅值减小。与刚性基础相同的是,Sr=1时各点竖向位移较Sr<1时有显著降低;当Sr<1时,初始孔隙率大,地基土体各点振动反应较初始孔隙率小时增加明显;当Sr=1时,初始孔隙率的大小对地基振动响应影响不大。
图13给出了不同饱和度下,土体初始孔隙率分别为0.36、0.6时,地基表面固相竖向位移幅值沿水平方向的分布曲线。
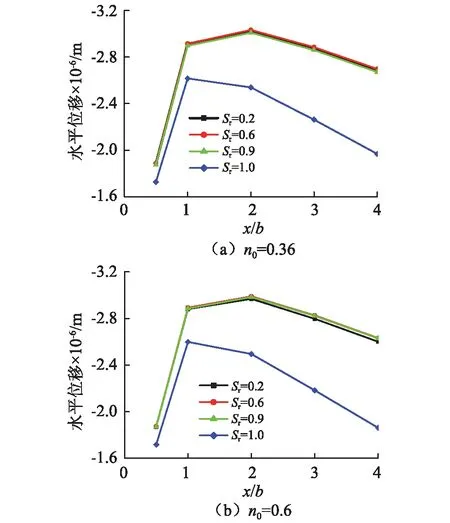
从图13中可以看出,与基础中心点下竖向位移类似,柔性基础地基表面的竖向位移幅值较刚性基础条件下相同位置处的要小;当Sr<1时,饱和度的变化对地表竖向位移幅值影响不如刚性基础条件下明显,初始孔隙率较大时,饱和度影响稍有增加,随着饱和度增加地表同一点处的竖向位移幅值减小;与刚性基础相同的是,Sr=1时各点竖向位移较Sr<1时有显著降低;当Sr<1时,初始孔隙率大,地基土体各点振动反应较初始孔隙率小时有所增加;当Sr=1时,初始孔隙率的大小对地基振动响应影响不大。因为是柔性基础,荷载作用范围内地表各点竖向位移随x/b的增加而衰减,并在0.5 图13 柔性基础地基表面竖向位移幅值沿水平方向分布曲线 图14 柔性基础地基表面水平位移幅值沿水平方向分布曲线 图14给出了不同饱和度下,土体初始孔隙率分别为0.36、0.6时,地基表面固相水平位移幅值沿水平方向的分布曲线。从图中可以看出,柔性基础地基表面的水平位移幅值较刚性基础条件下相同位置处的小;当Sr<1时,在两种初始孔隙率条件下,饱和度的变化对地表水平位移幅值影响均不明显。Sr=1时各点水平位移较Sr<1时有显著降低,尤其是在荷载作用范围外(x/b>1);初始孔隙率不同,地基表面相同点处水平位移幅值差别不大。说明柔性基础条件下,饱和度及初始孔隙率对地表水平位移影响有限。 针对目前非饱和土地基的振动响应研究刚刚起步,分析方法尚不完善,本文在现有的非饱和孔隙介质波动方程的基础上,采用解耦技术,建立非饱和多孔介质动力反应分析的显式有限元方法。 采用该方法,分别建立刚性和柔性条形基础作用下非饱和土地基振动模型,分析了在竖向均布脉冲荷载作用下,饱和度、孔隙率等因素对的非饱和土地基动力反应的影响。计算表明:①刚性基础条件下地基的振动明显高于相同条件下柔性基础地基振动,这与现有研究结果,随着基础柔性增加,地基动力柔度系数增加是一致的;②刚性基础条件下,Sr<1时,随着饱和度增加各点竖向位移减小,水平位移增大;Sr=1时各点竖向、水平位移均比Sr<1时明显减小,说明非饱和土中气相状态的存在与否对刚性基础条件下地基振动具有较为显著的影响。③柔性基础条件下,Sr<1时,饱和度对各点的竖向、水平位移影响有限;Sr=1时各点竖向、水平位移均比Sr<1时明显减小。④饱和度对地基振动的影响与土体的孔隙率有关,其他条件相同时,初始孔隙率高的,饱和度影响较大,且相同条件下地基动力反应大。 由于篇幅限制,本文只讨论了饱和度对各点振动位移的影响,对于非饱和土地基其他振动响应如动应力及孔隙流体压力分布等将在后续文章中讨论。
5 结 论
