不同拉压模量的非饱和土体自承载能力分析

于旭光

唐山工业职业技术学院 063299

引言

小孔扩张理论是研究关于柱形孔或球形孔扩张和收缩所引起的应力、孔隙水压力和位移变化的理论［1］，已经广泛应用于桩基础和地锚［2，3］、土体原位试验［4］以及隧道和地下开挖［5］等工程中，并且以上均涉及到评价岩体或土体的自身承载能力。赵均海等［6］提出了新的围岩自承载系数（即缩孔自承载系数）用于评价隧道围岩的自承载能力，相比于传统的抗力系数，虽然在形式上相同，但是比传统的抗力系数更有优势，由于新的围岩自承载系数考虑了初始地应力的影响，进而力的改变量与位移改变量的方向相同（指向洞内），并且解决了采用传统抗力系数求解无支护隧道抗力系数为0 这一有悖常识的问题；张常光等［7］在文献［6］基础上，提出了用于沉桩挤土孔扩张问题的扩孔自承载系数，并将缩孔和扩孔自承载系数进行了对比分析，但在扩孔自承载系数分析中研究对象为饱和土且未考虑土体抗拉和抗压特性的差异性。而目前在非饱和土地区由于沉桩挤土效应对桩周土体具有加固作用，合理利用可节约材料和费用，因此挤土桩在非饱和土地区普遍应用［8］。龚晓南［9］通过三轴压缩与三轴伸长试验表明土体抗压和抗拉特性差异较大，不可忽视。

因此，本文针对上述扩孔自承载系数研究不足，根据非饱和土统一强度理论，综合考虑材料的不同拉压模量、基质吸力以及强度非线性、中间主应力效应、剪胀特性等因素，对理想弹-塑性非饱和土体自承载系数进行理论推导和参数影响特性分析。

1 基本理论

1.1 平面应变条件下非饱和土统一强度理论

根据张常光等［10］建立的非饱和土统一强度理论，同时参考文献［11］建立平面应变条件下统一强度理论的方法，可得平面应变条件下非饱和土统一强度理论表达式为：

式中：c′、φ′分别为对应饱和土的有效黏聚力、有效内摩擦角；cs为非饱和土的吸附强度，其值cs＝ustanφb＝（ua－uw）tanφb，其中us为基质吸力，其值为（ua－uw），ua为孔隙气压力，uw为孔隙水压力，φb为与基质吸力（ua－uw）有关的吸力角；（σ1－ua）、（σ3－ua）分别为最大、最小净主应力；b 为选用不同强度准则的参数，取值范围为0≤b≤1。

1.2 非饱和土强度非线性

对于吸力角φb的取值，文 献［12 －17］指出：在高吸力范围内时，吸力角φb为基质吸力（ua－uw）的函数，且随基质吸力的增大而减小。比较典型的是S. L. Houston 等［16］提出的吸力角φb与基质吸力（ua－uw）的分段双曲线函数关系表达式为：

式中：（ua－uw）b为进气值，工程中常见取值范围为（0 ～50）kPa［16，18－19］；参数n 可由有效内摩擦角确定，即：1／n ＝－2.4598 ＋1.0225φ′；参数m由试验值确定［16，20］，并且文献［16］给出了12 种非饱和土的m 值，其取值范围为（0.46 ～31.5）kPa。

将式（2）代入式（1）可得到平面应变条件下考虑高基质吸力时强度非线性的非饱和土统一强度理论表达式。

2 非饱和土体自承载系数

对于具有不同拉压模量的柱形孔扩张问题，其力学模型见图1。设无穷远处受等值的初始地应力p0，柱形孔内表面均匀压力为pi，半径为ri，塑性区半径为rp。这里pi指的是沉桩施工中对桩周土体的挤压力。

图1 柱形孔扩张力学模型Fig.1 Mechanical model of cylindrical cavity expansion

文献［7］依据抗力系数的概念，提出了柱形孔扩张时土体自承载系数K表达式为：

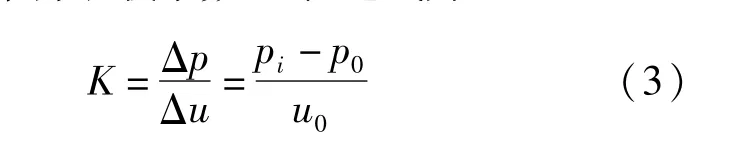
式中：Δp为柱形孔孔壁处压力的改变量；Δu 为柱形孔孔壁处位移的改变量，因开挖前柱形孔孔壁处无位移，故Δu 即为柱形孔孔壁处的实际位移u0。

对于沉桩施工对桩周土体扩张问题，可看成处于平面应变状态下的柱形孔扩张问题，随扩孔压力pi增大，孔壁周围土体逐渐由弹性状态进入塑性状态。

参考文献［7］求解思路，可得如下结果：

塑性区应力为：考虑不同拉压模量的弹性区应力和位移为［21］：

式中：α为拉压模量系数，其值为：

扩孔临界压力py和塑性区半径rp分别为：

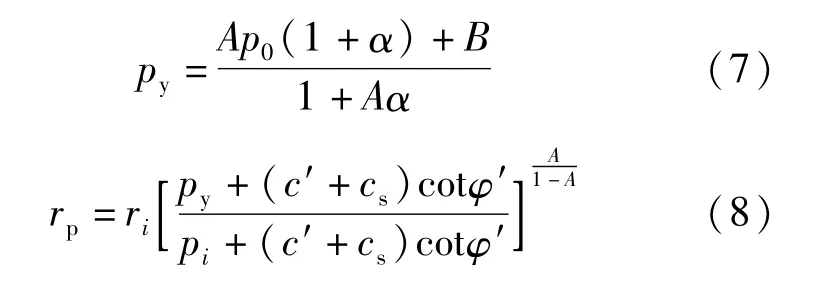
围岩塑性区位移u 和柱形孔孔壁处位移u0分别为：

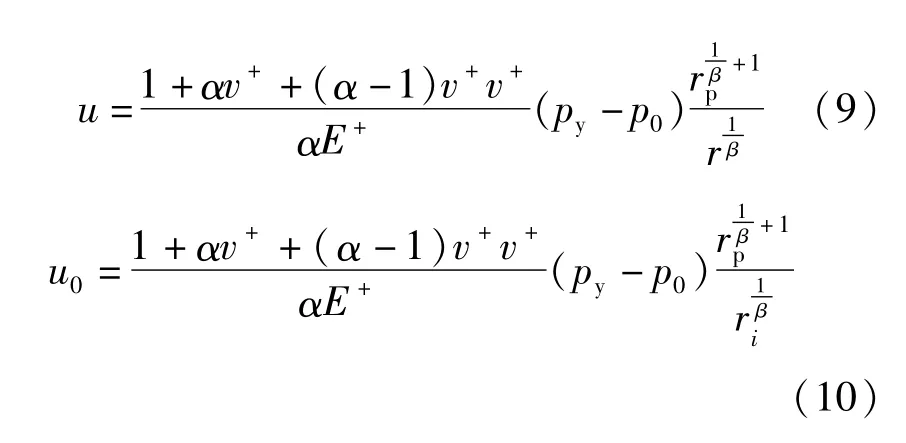
式中：β 为剪胀特性参数，其值为（1 ＋sinψ）／（1 －sinψ），其中ψ为剪胀角。

将式（8）和式（10）联立，然后代入式（3），可得到理想弹-塑性非饱和土体自承载系数为：

从式（11）可以看出，非饱和土体自承载系数K与初始地应力p0、孔壁压力pi、几何尺寸ri以及非饱和土体特性参数等有关。当非饱和土体完全处于弹性状态时，可将式（11）中孔壁压力pi替换扩孔临界压力py，可得到非饱和土体弹性自承载系数。

当ua－uw＝0 及E＋＝E－、ν＋＝ν－（即α ＝1）时，式（11）即为拉压模量相同时饱和土体自承载系数［7］。

3 本文理论解与有限元分析对比

为了验证本文理论解的正确性，选取文献［22］非饱和土体中排水条件下的计算参数，具体参数如下：E＋＝25MPa，ν＋＝0.3，c′＝38.816kPa，φ′＝20°，φb＝10°，（ua－uw）＝50kPa，ri＝0.05m，p0＝50kPa，pi＝150kPa。未给出的其他参数本文取值如下：依据文献［22］可知有限元分析得到的扩孔孔壁位移为0.28mm；剪胀角ψ 取为内摩擦角的二分之一［23］。从表1 可以看出，当b ＝0，α ＝1.0 时有限元分析与本文理论解误差不大，这是由于在有限元分析中采用Mohr-Coulomb 强度准则并且假设土体为均匀和各向同性材料。而在实际中应充分考虑b 和α，不同α 值求得的K值差异很大。本文只是通过一个简单算例进行了解释，鉴于非饱和土体的复杂性，应将文献［16］中的12 种非饱和土体进行现场试验来进行对比。

表1 理论解与有限元分析对比Tab.1 Comparison of theoretical solution and finite element analysis

4 算例及参数分析

本节主要探讨孔壁压力和非饱和土体特性参数对非饱和土体自承载系数的影响。

取非饱和土体的压缩模量E＋＝6.4MPa，压缩时泊松比ν＋＝0.2，有效黏聚力c′＝10kPa，有效内摩擦角φ′ ＝20°，吸力角φb＝12°，进气值（ua－uw）b＝25kPa，柱形孔半径ri＝0.5m，初始地应力p0＝78kPa［24］。

对体现强度非线性的吸力角φb取值一般有2种方法（见图2）：方法1 是在整个基质吸力范围内取一恒定的较小吸力角φb＝12°［15］；方法2 是在整个基质吸力范围内，按照进气值（ua－uw）b分成2 段（即式（2））。

图2 非饱和土强度非线性［15］Fig.2 Strength nonlinearity of unsaturated soil［15］

从图2 可以看出，在方法2 中非饱和土抗剪强度与基质吸力的关系曲线可以分为3 个区间：第1 个区间为FG段，此时吸力角φb等于有效内摩擦角φ′，非饱和土抗剪强度与基质吸力呈线性关系；第2 个区间为GM段，此时吸力角φb随基质吸力的增大而减小，在此区间，基质吸力增大对非饱和土抗剪强度的提高作用大于使吸力角φb减小对非饱和土抗剪强度的降低作用，因此会出现非饱和土抗剪强度逐渐增大，但增加速率越来越小，当基质吸力增大对非饱和土抗剪强度的提高作用等于使吸力角φb减小对非饱和土抗剪强度的降低作用时，到达最大值M点；第3 个区间为MN段，此区间表示基质吸力增大对非饱和土抗剪强度的提高作用小于使吸力角φb减小对非饱和土抗剪强度的降低作用，此时非饱和土抗剪强度从M点开始逐渐下降。

从上面可以看出，采用方法1 计算较简单，采用方法2 稍复杂但是比方法1 计算精确。以下分析计算中，在4.1 ～4.3 节分析中采用方法1，在4.4 节分析中将同时采用这两种方法来进行计算，进而对比这两种方法之间的差异。

4.1 孔壁压力影响

孔壁压力pi和初始地应力p0的相对大小直接决定柱形孔所处的应力状态。图3a 给出了当α ＝1.0，β ＝2，b ＝0.5 时，不同基质吸力（ua－uw）情况下非饱和土体自承载系数K 与pi／p0的关系曲线；图3b 给出了当（ua－ uw）＝25kPa，β ＝2，b ＝0.5 时，不同拉压模量系数α情况下非饱和土体自承载系数K与pi／p0的关系曲线。

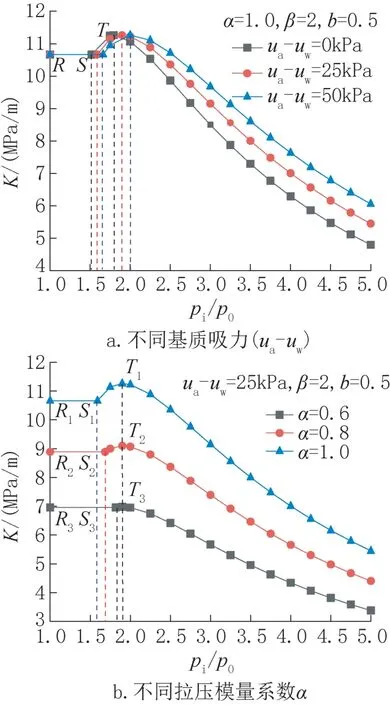
图3 孔壁压力对非饱和土自承载系数的影响Fig.3 Effect of wall pressure on self-bearing coefficient of unsaturated soil

从图3a可以看出，孔壁压力pi对非饱和土体自承载系数K的影响以S 点和T点为界分成3段：S点前的RS 段代表处于弹性变形状态，此时K ＝10.67MPa／m，为恒值；S 点之后的ST 段代表塑性挤压阶段，代表孔壁压力pi增加的速率大于孔壁处位移u0增加的速率，此时非饱和土体自承载系数K逐渐增大，当到达T点后处于最大值，接着进入塑性流动阶段，此时孔壁压力pi增加的速率小于孔壁处位移u0增加的速率，此时非饱和土体自承载系数K逐渐减小。

从图3a 还可以看出，不同基质吸力（ua－uw）下的S 点位置不同，随着基质吸力（ua－uw）增加，S点逐渐右移，说明需要更大的孔壁压力pi才能使非饱和土体（当（ua－uw）＝0 时已变为饱和土体）进入塑性变形状态，即非饱和土体会比饱和土体推迟进入塑性变形时机，会更有利于自承载能力发挥。进入塑性变形阶段后，在塑性挤压阶段（ST 段），非饱和土体比饱和土体的自承载能力低，但相差不大；而在塑性流动阶段，非饱和土体比饱和土体的自承载能力高，且随着pi／p0和基质吸力（ua－uw）增加，自承载系数K增大显著，表明在此阶段若采用饱和土体的自承载系数计算结果会严重低估非饱和土体的自承载能力，当非饱和土体的基质吸力（ua－uw）越大，会使计算结果越保守。

从图3b可以看出，不同拉压模量系数α 下的非饱和土体的自承载系数K 差异明显，随着α的减小，非饱和土体自承载系数K减小，且弹性变形阶段和塑性变形阶段分界点（即点S1、S2、S3）逐渐右移。在塑性变形阶段中，当0 ＜α ＜0.6时塑性挤压阶段将会逐渐消失，会由弹性变形阶段直接进入塑性流动阶段。另外，还可以看出，采用拉压模量相同（α ＝1.0）的自承载系数来计算会高估非饱和土体的自承载能力，使计算结果偏于不安全。

4.2 拉压模量系数影响

对于土体来说，其压缩模量要比拉伸模量大得多。图4a 给出了当pi＝2py，β ＝2，b ＝0.5时，不同基质吸力（ua－uw）情况下非饱和土体自承载系数K 与α 的关系曲线；图4b 给出了当pi＝2py，β ＝2，（ua－uw）＝25kPa 时，不同参数b情况下非饱和土体自承载系数K 与α 的关系曲线。

图4 拉压模量系数对非饱和土自承载系数的影响Fig.4 Effect of tension-compression modulus coefficient on self-bearing coefficient of unsaturated soil

从图4a可以看出，随着α 增加，非饱和土体自承载系数K 呈非线性增大。当（ua－uw）＝25kPa时，α ＝1.0 时的非饱和土体自承载系数K是α ＝0.2 时的6.2 倍，可见非饱和土体自承载系数K受α影响较大。另外，在α 取相同值时，非饱和土体自承载系数K均随基质吸力（ua－uw）增加而增大，因此，在不同α 值时，若采用（ua－uw）＝0（此时对应于饱和土体）来计算自承载系数均会低估非饱和土体的自承载能力，会使计算结果偏于保守。

从图4b 可以看出，随着参数b 的增加，非饱和土体自承载系数K均呈非线性增大。当α分别为0.2、0.6、1.0 时，b ＝1 时的自承载系数比b ＝0 分别增大了12.2%、11.1%、10.3%，可见，自承载系数K增大幅度随α增大而变小。

4.3 中间主应力和剪胀影响

不同的非饱和土体的中间主应力σ2效应和剪胀特性也不同。图5 给出了当pi＝2py，α ＝0.2时，不同基质吸力（ua－uw）及剪胀特性参数β下非饱和土体自承载系数K与b的关系曲线。

从图5 可以看出，当β 和（ua－uw）相同时，随着参数b的增加，非饱和土体自承载系数K增大，但增大趋势逐渐变缓。当β ＝3、（ua－uw）＝25kPa时，b ＝1 时的自承载系数比b ＝0 时增大了9.9%，可见采用Mohr-Coulomb准则（即b ＝0）会使计算结果偏于保守，应充分考虑非饱和土体的中间主应力σ2效应，但增大幅度不大，说明在沉桩挤土扩张问题中，中间主应力σ2效应不太显著。当b和（ua－uw）相同时，随着参数β 的增加，非饱和土体自承载系数K也增大，但增大趋势也是逐渐变缓。比如当b ＝1和（ua－uw）＝25kPa时，β ＝3 时的自承载系数比β ＝1 时增大了98.8%，可见不考虑非饱和土体的剪胀（即β ＝1）会严重低估非饱和土体自承载系数。当β 和b 相同时，非饱和土体自承载系数（（ua－uw）＝25kPa）均大于饱和土体自承载系数（（ua－uw）＝0kPa）。

图5 中间主应力和剪胀对非饱和土自承载系数的影响Fig.5 Effect of intermediate principal stress and dilatancy on self-bearing coefficient of unsaturated soil

4.4 强度非线性影响

在高吸力范围内时（即基质吸力大于进气值（ua－uw）b），非饱和土的强度具有明显的非线性，本小节取pi＝2py，β ＝2，b ＝0.5，图6 给出了当α取0.6、0.8 和1.0，分别采用方法1 和方法2 时非饱和土体自承载系数K与（ua－uw）的关系曲线。其中在方法1 中采用的吸力角在整个基质吸力范围内恒为φb＝12°。在方法2 中，当基质吸力不大于进气值25kPa 的低吸力范围内时，吸力角φb＝φ′ ＝20°；当基质吸力大于进气值25kPa的高吸力范围内时，吸力角φb采用双曲线模型即式（2）计算，参数n 根据1／n ＝－2.4598 ＋1.0225φ′可得n ＝0.0556，参数m分别取2.5kPa、5kPa、10kPa和20kPa，用来反映高吸力下吸力角不同的变化速率。

图6 强度非线性对非饱和土自承载系数的影响Fig.6 Effect of strength nonlinearity on self-bearing coefficient of unsaturated soil

从图6 可以看出，采用方法1 计算的结果在进气值25kPa前后无拐点，在整个基质吸力范围内非饱和土体自承载系数K与（ua－uw）近似呈直线增大。采用方法2 计算的结果以进气值25kPa为界分成2 段：不大于进气值25kPa 的低吸力范围内时，非饱和土体自承载系数K与（ua－uw）近似呈直线增大，与参数m 无关；大于进气值25kPa的高吸力范围内时，非饱和土体自承载系数K随（ua－uw）增大呈微弯直接增大，且参数m越小，非饱和土体自承载系数K 增大幅度越小，实际上在此区间的曲线正好反映了基质吸力对非饱和土抗剪强度的提高以及使吸力角减小对抗剪强度降低的双重影响，并且计算结果对应图2 中的GM段，即基质吸力增大对非饱和土抗剪强度的提高作用大于使吸力角φb减小对非饱和土抗剪强度的降低作用，因此非饱和土体自承载系数K一直增大，但增加幅度越来越小。另外，还可以看出，参数m越小，在进气值25kPa前后拐点越明显，明显出现与方法1 得出的曲线会相交，其交点处对应的基质吸力值几乎与α 值无关（比如当m分别取2.5kPa、5kPa 时，3 个不同α 值对应交点处的基质吸力（ua－uw）均分别为60kPa、97.5kPa），而与m 密切相关，且随着m 增大，相交点逐渐右移，并且m越大，非饱和土体自承载系数K越大。

需要说明的是，当m取值较小时，在高吸力范围内，方法2 与方法1 得到的非饱和土体自承载系数K与（ua－uw）的关系曲线会相交，从而在基质吸力相交点处将高吸力范围又分成2 段，比如当m ＝2.5kPa 时，在相交点处基质吸力（ua－uw）＝60 kPa，若基质吸力处于25 ＜（ua－uw）≤60时，若采用方法1 来计算会低估非饱和土体自承载能力，所得结果偏于保守；若基质吸力处于60 ＜（ua－uw）≤100 时，若采用方法1 来计算会高估非饱和土体自承载能力，所得结果偏于不安全。而当m取值较大时（比如本小节m ＞5kPa），在整个高吸力范围内，采用方法1 来计算均会低估非饱和土体自承载能力。因此，当m取值较小时，在计算时应谨慎选择较简单的方法1。

5 结论

1.本文根据非饱和土统一强度理论，建立的理想弹-塑性非饱和土体自承载系数（式（11））是有序理论解的集合，可以充分考虑材料的不同拉压模量、基质吸力以及强度非线性、中间主应力效应、剪胀特性等综合因素。当拉压模量相同、基质吸力为0 时可退化为饱和土的计算结果［7］，因而本文解具有更广泛的适用性。

2.非饱和土体自承载系数K 能反映非饱和土体自身的承载能力且物理意义明确，其值与初始地应力、孔壁压力、几何尺寸、以及非饱和土体特性参数等相关。

3.孔壁压力对非饱和土体自承载系数K 具有显著影响，当拉压模量系数较大时（本文即0.6≤α≤1.0），非饱和土体自承载系数K以扩孔临界压力和峰值点为界分成3 段，弹性变形阶段、塑性挤压阶段和塑性流动阶段；当拉压模量系数较小时（本文即0 ＜α ＜0.6），非饱和土体自承载系数K以扩孔临界压力为界分成2 段，弹性变形阶段和塑性流动阶段。非饱和土体自承载系数K 均随拉压模量系数α 和参数b 呈非线性增大，随剪胀特性参数β呈微弯增大。当m取值较小时（比如本文m≤5kPa），在计算时应谨慎选择恒定较小吸力角的方法1，建议采用分段双曲线吸力角的方法2；当m 取值较大时（比如本文m ＞5kPa），采用恒定较小吸力角的方法1 则偏于保守。

4.对于沉桩施工、静力触探等问题，其桩端、探头等周围土体呈现球形孔扩张，可采用与本文类似的分析方法。