一种基于标准差的K-medoids聚类算法
2020-08-12邓玉芳张继福
邓玉芳,张继福
(太原科技大学 计算机科学与技术学院,山西 太原 030024)
0 引 言
聚类分析是数据挖掘[1]、模式识别[2]等领域的重要研究内容之一,在识别数据的内在结构方面具有重要的作用[3],并已广泛地应用在金融分析、疾病诊断、假新闻检测[4]、农业灾害预测等实际问题中。聚类分析是一种常用的无监督数据挖掘方法[5],可将数据集划分成若干个簇,目标是使在同一个簇里的数据相似度尽可能得高,不同的簇之间的数据相似度尽可能得低,由此根据数据信息将数据划分为若干簇,揭示数据的原始分布。K-medoids算法[6]是一类基于划分的聚类分析方法,具有对孤立点敏感度低和良好的鲁棒性等优点,并已得到了广泛应用。
目前,大多数K-medoids聚类算法,由于初始聚类中心点的选取和中心点迭代更新等原因,存在着聚类精度和效率较低,且需要额外设置参数等不足。文中利用标准差选择候选初始聚类中心,给出了一种K-medoids聚类分析算法。该算法首先利用标准差定义了初始中心点候选集度量公式,有效地避免密集程度较低的样本点,尤其是孤立点作为初始聚类中心;其次采用从两个初始中心点逐步增加中心点直到K个中心点的方式,从初始中心点候选集中确定初始中心点,避免初始中心点选择在同一个聚类簇;然后按照将数据样本归属于最近的中心点的原则,形成初始聚类簇;再次更新聚类中心点,直到与上一次的聚类误差平方和相同,形成聚类簇;最后采用UCI数据集和人工数据集进行实验,验证了该聚类算法的有效性。
1 相关工作
聚类分析是将数据集划分成若干个簇,在簇里的数据对象的相似度尽可能高,不同簇之间的数据对象的相似度尽可能低。常用的聚类分析算法大致分为:基于划分的方法、基于密度的方法、基于层次的方法、基于网格的方法、基于模型的方法[7],以及基于子空间的方法[8-10]。K-medoids算法由于是以簇中心的实际样本对象作为簇中心点,从而有效地降低了对于噪声数据和孤立点的敏感性。K-medoids聚类算法在选择初始中心点时,有可能选为离散点或异常点,容易使聚类过程陷入局部极值,同时也需要不断地迭代更新聚类中心点,因此聚类效果和效率较差。
K-medoids聚类算法经典的PAM算法思想是:选取数据集中实际样本对象来代表类簇中心,首先随机选择K个初始中心点,将剩余的所有非中心点样本分配到与其最为相似的聚类簇中,计算聚类代价函数。其次选取一个非中心点样本作为新的中心点替换原来的中心点,然后计算替换中心点后的聚类代价函数,如果聚类代价函数减少,则由新的中心点替换原来的中心点,形成新的K个中心点,按此方式不断地进行中心点的迭代更新,直到聚类代价函数不再降低,没有可以替换的中心点为止。目前K-medoids聚类分析的研究成果主要集中在如下三方面。
(1)初始聚类中心点选取。
Park等人提出了快速K-medoids算法[11],按照密度排序,采用前K个样本点作为初始中心点。在更新中心点时采用了K-means,相比PAM算法在计算量上有所降低,在效率上有所提高。但是因为采用的选取初始中心点的方式会导致选取的初始中心点可能在一个聚类簇,因此不能很好地选择出分布在不同簇的初始中心点,使得聚类效果的准确性不高。马箐等人提出了基于粒计算的K-medoids聚类算法,采用了粒度概念[12],该聚类算法给出了新的样本相似度函数,并定义了类簇中心,利用等价关系产生粒子,然后依据粒子包含样本的数据量大小来定义粒子密度,最后选择密度较大的前K个粒子的中心样本点作为K-medoids聚类算法的初始聚类中心,改进K-medoids聚类算法的初始中心随机选取对聚类结果的影响,从而提高K-medoids聚类算法的效率。谢娟英等人[13]提出了密度峰值优化初始中心的K-medoids聚类算法,该聚类算法首先需要做出决策图,然后根据决策图来确定初始中心点,但是同样也会出现初始中心点选择在同一个簇的情况。Yu等人[14]提出了INCK聚类算法,该聚类算法从部分符合要求的数据样本中确定聚类中心,提高了聚类结果的准确性,但是在找寻符合要求的样本时存在参数的选取问题,而参数的选取会影响聚类结果的准确性。为此,文中定义了新的初始中心点候选集,在原始数据上进行聚类。
(2)迭代更新聚类中心点。
Chu等人[15]推导了一个新的不等式,该不等式可用于最近邻搜索问题。提出了基于新不等式,先前的中心点指标,内存利用,三角形不等式准则和部分距离搜索的四种基于K-medoids算法的搜索策略。颜宏文等人[16]提出了基于宽度优先搜索的K-medoids聚类算法。该算法利用粒计算初始化获取K个有效粒子,从粒子中选出K个中心点作为初始中心点。之后分别对K个粒子中的对象建立以中心点为根节点的相似对象二叉树,通过宽度优先搜索遍历二叉树迭代出最优中心点。宋红海等人[17]提出了基于优化粒计算下微粒子动态搜索的K-medoids聚类算法。该算法是在优化的粒计算前提下,提出了基于微粒子动态搜索策略,以初始中心点作为基点,形成一个微粒子,在微粒子内部,采用离中心点先近后远的原则进行搜索,有效地缩小搜索范围,提高了聚类准确率。余冬华等人[18]提出的SPAM算法中在总结的三角不等式的基础上提出了2个加速定理,其中一个定理适用于一次交换一个中心点的情况,另一个加速定理是第一个定理的扩展,可适用于一次交换多个中心点的情况。同时SPAM算法存储样本到其聚类中心的距离和中心点之间的距离,以提高效率。
(3)聚类分析的并行化。
在处理海量数据信息时面临的内存容量和CPU处理速度的问题上通常采用并行化来处理。Jiang等人[19]实现了基于Hadoop分布式计算平台上的K-medoids聚类。每个提交的作业都有许多迭代的MapReduce程序,在Map阶段每个样本被分到距离中心最相似的那个簇。在comebine阶段计算每个簇的中心点,在reduce阶段计算新的中心点。当新中心点和原来的中心点相同时停止迭代。Zhao等人[20]通过引入Canopy算法和Max-Min距离算法改进了原始的K-Medoids算法,并选择了K个点作为聚类的初始中心。然后使用MapReduce计算框架来并行化算法,改进的聚类算法不仅具有良好的加速性能,而且提高了聚类的准确性和收敛性,在处理大规模数据方面具有很大的性能优势。赖向阳等人提出了一种MapReduce架构下基于遗传算法的K-Medoids聚类[21]。利用遗传算法的种群进化特点来改进K-Medoids算法的初始中心敏感的问题,然后将遗传K-Medoids算法再结合MapReduce并行,提高算法效率。王永贵等人提出了一种基于Hadoop的高效K-Medoids并行算法[22]。该算法通过改进初始中心点选择和中心点替换策略这两个方面提高聚类精度。利用Hadoop计算平台结合基于Top K的并行随机抽样策略,实现了高效稳定的K-Medoids并行算法,之后又通过调整Hadoop平台,实现了算法的进一步优化。
综上所述,近些年来很多研究者都对聚类分析做了一定的研究。K-medoids算法作为一种基于划分的聚类分析方法,以实际样本点作为簇中心点,从而有效地降低了对于噪声数据和孤立点的敏感性,具有良好的鲁棒性。但是在选择初始中心点时,有可能选为离散点或异常点,使得聚类准确性不高。迭代更新中心点需要大量距离计算,使得聚类效率较低。
2 基本概念
聚类分析任务是将给定数据集划分成多个簇,使簇中的数据对象尽可能相似,不同的簇之间的数据对象差异性大,可采用欧氏距离来衡量数据对象之间的相似性[23]。假设数据集X={x1,x2,…,xn},样本数为n,每个样本的维数是p,第i个样本的第a个属性值表示为xia。参照文献[13]两个样本间的欧氏距离,给出样本xi与xj之间的欧氏距离,公式如下:
(1)
其中,d(xi,xj)表示样本xi与xj的距离,i=1,2,…,n,j=1,2,…,n。
参照文献[14],聚类误差平方和、数据集的标准差和每个样本的标准差公式分别定义如下:
(2)
其中,oi表示第i个簇的簇中心点,ci表示第i个簇,而x是属于第i个簇的样本点。数据集的标准差定义如下:
(3)

每个样本的标准差公式如下:
(4)
其中,vi就是每个样本的标准差值。
3 基于标准差的K-medoids聚类分析
3.1 初始中心点候选集
K-medoids聚类算法中初始中心点的选取影响最终的聚类结果。初始中心点选择在接近最终聚类中心点区域时,聚类结果的准确性相对较高且迭代更新中心点的次数较少。当初始中心点选择为严重偏离最终聚类中心区域的样本或者孤立点时,聚类过程容易陷入局部极值,聚类结果准确性较低且迭代更新中心点的次数较多。在K-medoids聚类算法中,初始中心点选择已成为提高聚类分析效果和效率的关键因素。
标准差在概率统计中最常使用统计分布程度上的测量,标准差定义为方差的算术平方根,反映数据的离散程度。标准差越小,反映数据分布比较密集,标准差越大,反映数据分布比较离散。聚类中心点的密集程度是较高的,所以中心点样本的标准差相对是较小的。相反的孤立点样本的密集度是较低的,孤立点样本的标准差相对是较大的。对于上一章节给定的数据集X,依据式(3)和式(4),将每个样本xi的标准差vi与整体数据集的标准差v进行比较,当vi小于v时,表明xi在分布密集程度相对较高的区域,因而成为聚类中心点的可能性要大;当vi大于v,表明xi在分布密集程度相对较低的区域,因而成为初始中心点的可能性要低。但是不能排除当vi略大于v时,样本xi是中心点的可能性,所以以大于v的所有样本的平均标准差作为初始中心点候选集的上界。从而既可以使密集程度较大的样本点在初始中心点候选集内,又可以使离散程度不太大的样本点也在初始中心点候选集里。
为了避免孤立点或者密集度较低的样本点被选为初始中心点,同时也为了使初始中心点被选为密集度较大的样本点,定义了初始中心点候选集,以进一步提高聚类的效果和效率。当样本的标准差小于超出数据集标准差的所有样本的平均标准差时,该样本点就有可能是初始中心点,初始中心点候选集sm的定义如下:
sm={xi|vi≤v',i=1,2,…,n}
(5)
其中,v'是vi大于v的所有vi的均值。
在K-medoids聚类分析中,不必从全部数据对象中选择初始中心点,仅从初始中心点候选集中选择即可,从而有效地提高了聚类中心点选取效率和效果。
3.2 聚类分析
在K-medoids聚类算法中,初始中心点选择尤为重要。在初始中心点的选取上,为了避免选取到孤立点作为初始中心点,同时又为了选取到密集程度较大的样本点作为初始中心点,文中利用式(5)定义的初始中心点候选集,从初始中心点候选集选取初始中心点,并迭代更新,其聚类过程参考INCK聚类算法由如下两步来实现。
首先在初始中心点候选集中选取两个初始中心点,并迭代更新两个初始中心点。在选择第一个初始中心点o1时,选取距离到所有样本点距离之和最小的样本点作为中心点,公式如下:
(6)
其中,样本xi到所有样本点的距离之和di的公式如下:
(7)
第二个初始中心点o2的选取为初始中心点候选集中距离第一个初始中心点最远的样本点,使初始中心点尽可能地选择在不同的聚类簇中,避免出现在同一聚类簇里,公式如下:
(8)
然后按照就近原则聚类,把所有的样本点归属于距离最近的中心点,计算聚类误差平方和,之后更新每个簇中心,使每个簇内新中心点距离其簇中所有样本的距离之和最小,公式如下:
(9)
其中,cj表示第j个聚类簇,xl要和xi一样是属于cj,如果xl不属于cj,则不将其与xi的距离算在内。用新中心点代替原中心点,然后聚类计算聚类误差平方和,若与上一次聚类误差平方和一样则不再更新中心点,否则继续更新中心点。
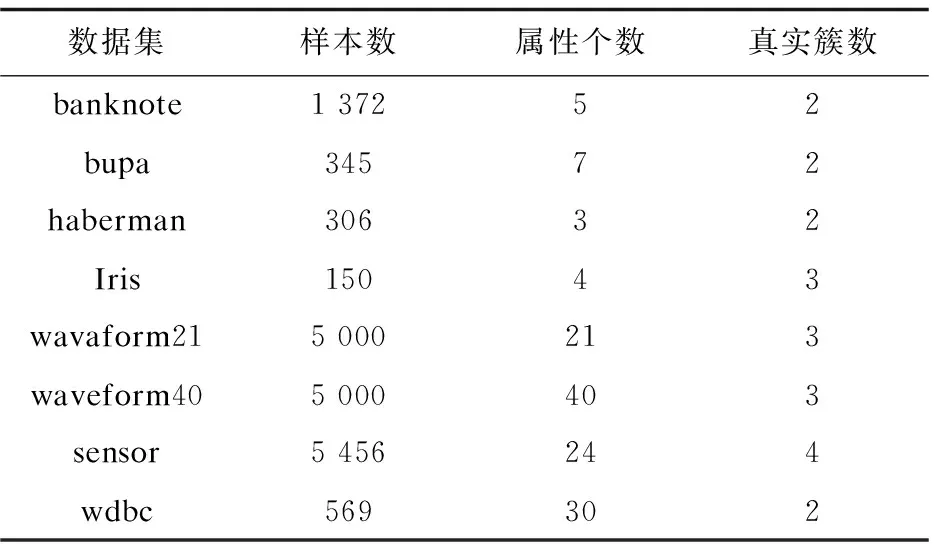
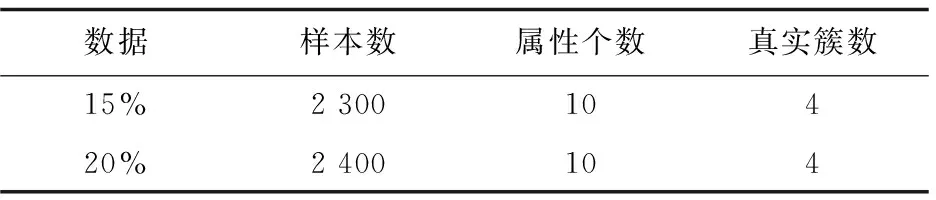
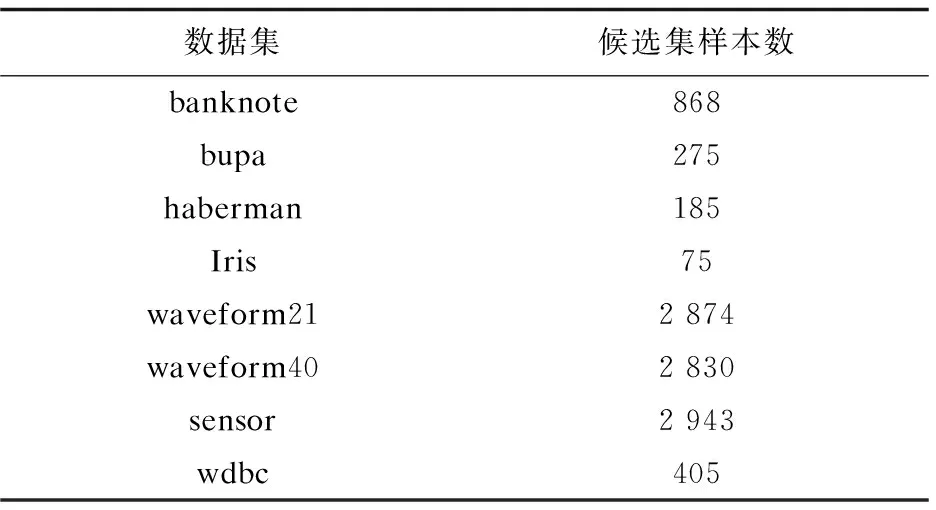
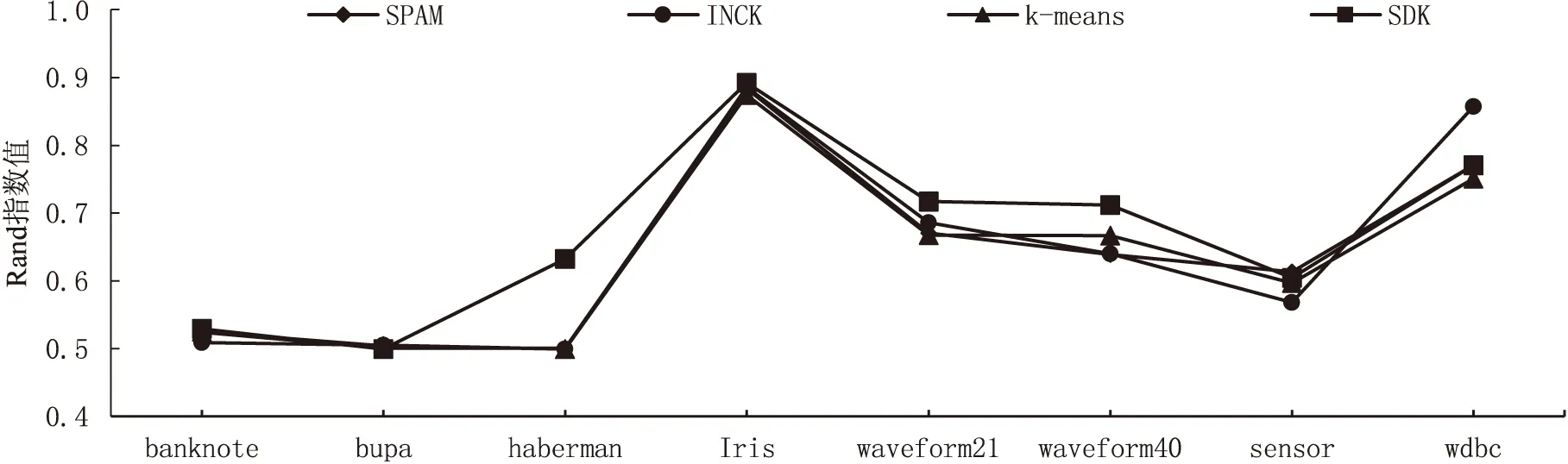
其次从初始中心点候选集中,选取其余的k-2个初始中心点。假设已经得到g(2≤g (10) (11) 然后聚类迭代更新中心点。按此方式逐步增加初始中心点直到确定k个中心点,并得到最终聚类结果。 根据上一小节聚类分析的基本思想,基于标准差的K-medoids聚类分析算法伪代码描述如下所示。 算法1:SDK聚类算法(standard-deviation-based K-medoids clustering algorithm) 输入:数据集X,簇数k 输出:k个聚类簇 (1)sm=getsm() (2)fori=1 tondo (3) forj=1 tondo (4)根据式(7)得到di (5) end for (6)end for (7)fori=1 tosdo (8)根据式(6)得到第一个初始中心点o1,s为初始中心点候选集大小 (9)end for (10)fori=1 tosdo (11)根据式(8)得到第二个初始中心点o2 (12)end for (13)Cluster() (14)fori=1 tondo (15)按照式(2)计算聚类误差平方和E (16)end for (17)Update(); (18)ifk>2 then (19) forg=2 tok-1 do (20) forj=1 tosdo (21)根据式(10)和式(11)得到第g+1个初始中心点 (22) end for (23) Cluster(); (24) forh=1 tondo (25)按照式(2)计算聚类误差平方和E (26) end for (27) Update(); (28) end for (29)end if 算法2:getsm() 输入:数据集X 输出:初始中心点候选集sm (1)fori=1 tondo (2) forj=itondo (3)计算得到样本间距离d(xi,xj) (4) end for (5)end for (6)fori=1 topdo (7) forj=1 tondo (9) end for (10)end for (11)fori=1 tondo (12)根据式(3)得到数据集标准差v (13)end for (14)fori=1 tondo (15) forj=1 tondo (16)根据式(4)得到每个样本点的标准差值vi (17) end for (18)end for (19)fori=1 tondo (20)根据式(5)得到sm; (21)end for 算法3:Update() 输入:g个中心点 输出:更新后的g个中心点和g个聚类簇 (1)While true do (2) fori=1 tondo (3) forj=1 tondo (4)按照式(9)找到更新后的中心点 (5) end for (6) end for (7) Cluster(); (8) forh=1 tondo (9)按照式(2)计算聚类误差平方和newE (10) end for (11) if newE==E then (12) break; (13) else (14) E=newE (15) end if (16)end while 算法4:Cluster() 输入:g个中心点 输出:g个聚类簇 (1) fori=1 tondo (2)d=d(xi,o1) (3) setlabeli=1 (4) forj=2 tokdo (5) newd=d(xi,oj) (6) if newd (7) setlabeli=j (8)d=newd (9) end if (10) end for (11) end for 在SDK聚类算法中,由算法2计算样本间距离的时间复杂度是o(n2),计算均值的时间复杂度是o(np),计算数据集的标准差的时间复杂度是o(n),计算所有样本的标准差的时间复杂度是o(n2),计算初始中心点候选集的时间复杂度是o(n),在算法1中计算di的时间复杂度是o(n2),选取初始中心点的时间复杂度是o(ks)。在算法4中,样本聚类的时间复杂度为o(nk),因此整体的聚类时间复杂度是o(nk2),在算法3中,假设更新中心点的最大迭代次数是t次,则更新中心点的时间复杂度是o(tn2),所以整体的更新中心点的时间复杂度为o(tkn2),因此SDK聚类算法的整体的时间复杂度是o(n2+np+n+n2+n+n2+ks+nk2+tkn2),最终时间复杂度表示为o(n2+tkn2+nk2)。 实验环境:Intel(R) Core(TM) i5-8265U CPU,8 G内存,windows10操作系统,eclipse作为开发平台,采用java语言实现SDK聚类算法。文中为验证SDK聚类算法的准确性以及鲁棒性,选用SPAM聚类算法,INCK聚类算法和经典的聚类算法k-means[24]在UCI数据集和人工数据集上进行实验验证。在对准确性的验证上采用了Rand指数还有F-measure值这两个评价指标。在验证SDK聚类算法的聚类效率时,与同样是K-medoids聚类算法的SPAM聚类算法、INCK聚类算法进行实验对比。在实验中SDK聚类算法、SPAM聚类算法以及经典k-means聚类算法的参数只需要k值,INCK聚类算法除了需要设定参数k值外,还需要一个额外的参数λ。 文中在实验中采用了UCI数据集,用来分析比较不同聚类算法的准确性和效率。在实验中采用的所有数据集的名称,数据的样本数,样本属性个数和真实的簇数如表1所示,其中sensor表示的是sensor_readings_24数据集。同时为了实验分析聚类算法的鲁棒性,采用了Matlab工具,随机生成了5组符合正态分布的人工数据集。在每组数据集分为4类,每类有500个数据样本,属性维度是10维的基础上,分别增加15%、20%、25%、30%、35%的噪声数据,从而形成5组人工数据集。表2为生成人工数据集的各种具体参数。按照表2给出的参数,随机生成了5组人工数据集,生成的5组人工数据集的具体的样本数,属性个数以及真实的簇数如表3所示。 表1 UCI数据集 表2 生成人工数据集的参数 表3 人工数据集 续表3 在SDK聚类算法中,由于采用了初始中心点候选集,所以聚类初始中心点选择不必从全部的数据样本中去确定,并且更为准确且有效。在实验验证中各个数据集的初始中心点候选集的样本个数如表4所示。 表4 初始中心点候选集 由表4可以看出,在实验中采用的所有数据集的初始中心点候选集样本数相较于原来整体数据集都减少了,从而在确定初始中心点时,不必从全体数据中寻找,减少了计算量,有效地提高了聚类效率。 为了验证SDK聚类算法的聚类效果,实验采用SDK聚类算法与SPAM聚类算法和INCK聚类算法以及k-means聚类算法在UCI数据集上进行了聚类精度的实验对比,其中实验结果数据采用了各算法运行10次的平均值。 从图1和图2的结果可以看出,无论是Rand指数还是F-measure值,表现最好的是SDK聚类算法,因此整体上,聚类的准确性最高的是SDK聚类算法。SDK聚类算法的聚类准确性相对较好主要是因为在对初始中心点的选取上,避免了选取孤立点为初始中心点,同时又尽可能地避免选取的初始中心点在同一个簇的情况,并且使初始中心点选在密集度相对较高的样本上,因而聚类准确性上表现较好。 图1 真实数据集上Rand指数的值 图2 真实数据集上F-measure的值 采用表1所示的UCI数据集,与同样是K-medoids算法的SPAM聚类算法和INCK聚类算法进行实验对比,验证SDK聚类算法的效率。实验结果如表5所示,其中取10次运行结果的平均值作为实验结果。 由表5可知,SDK聚类算法效率是最高的,而SPAM聚类算法效率是最差的,INCK聚类算法的效率居中。其主要原因是SDK聚类算法采用了初始中心点候选集的方式,确定中心点的时候不必从全部样本中选择,在更新中心点时和INCK聚类算法一样采用了快速K-medoids的方式,而SPAM聚类算法采用的是PAM聚类算法的中心点更新方式,从全部数据样本中查找中心点,所以SDK聚类算法在计算量上相对减少。除此之外,SDK聚类算法和INCK聚类算法采用了存储样本之间距离的方式,之后用到直接调用即可。SPAM聚类算法虽然也采用存储距离的方式,但是只存储样本点到其中心点的距离和中心点之间的距离,在之后用到其他两个样本之间的距离时都要重新计算。因此SDK聚类算法和INCK聚类算法都减少了不必要的距离的重复计算,而SPAM聚类算法需要重复计算距离。所以整体上SDK聚类算法和INCK聚类算法的效率都要比SPAM聚类算法要高,而文中SDK聚类算法的效率是最高的。 表5 聚类算法运行时间 s 为了验证SDK聚类算法的鲁棒性,采用表3所示的人工数据集,将SDK聚类算法,SPAM聚类算法,INCK聚类算法和k-means聚类算法进行了实验对比分析,其中实验结果选取了各算法运行10次结果的平均值。表6是Rand指数的实验结果,表7是F-measure的实验结果。 表6 人工数据集上的Rand指数 表7 人工数据集上的F-measure 从表6和表7可知,在4个聚类算法中,SDK聚类算法和SPAM聚类算法的鲁棒性表现相近且表现较好,INCK聚类算法的鲁棒性是最差的。SDK聚类算法的鲁棒性保持良好的主要原因是SDK聚类算法采用了初始中心点候选集,在选取中心点的时候,尽量避免不合适的数据被选为中心点。 利用了标准差反映数据分布离散程度的原理,定义了初始中心点候选集,从初始中心点候选集中选取初始中心点,避免孤立点或者密集度较低的样本点被选为初始中心点,同时也使初始中心点选为密集度较大的样本点。在UCI数据集及人工数据集上进行了实验验证,其实验结果验证了该算法的有效性。下一步的工作主要是对SDK聚类算法的并行化。
3.3 聚类分析算法
3.4 时间复杂度分析
4 实验结果及相关分析
4.1 数据集


4.2 初始中心点候选集
4.3 聚类精度
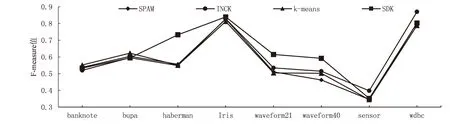
4.4 聚类效率
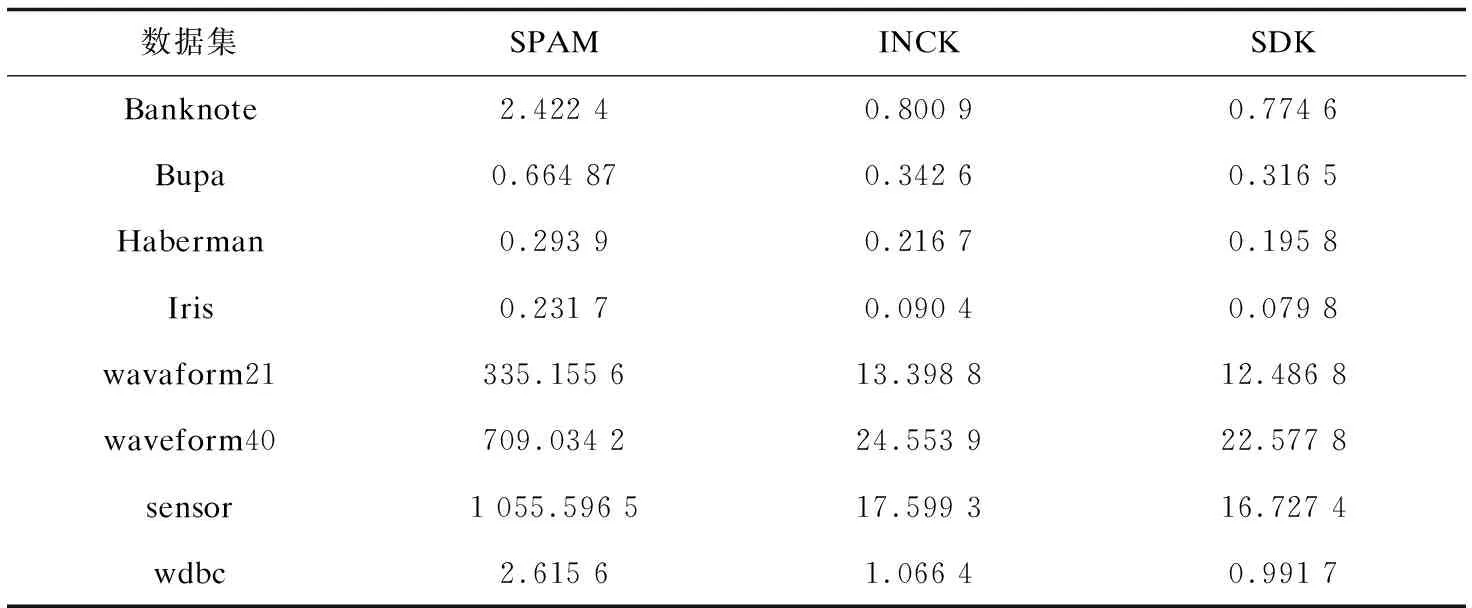
4.5 聚类鲁棒性
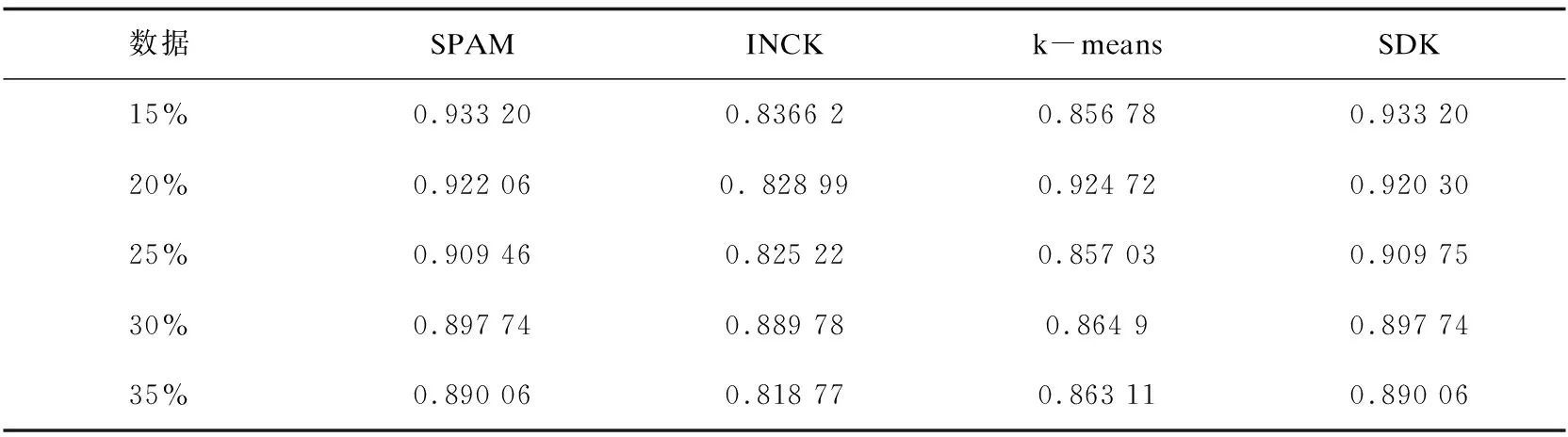
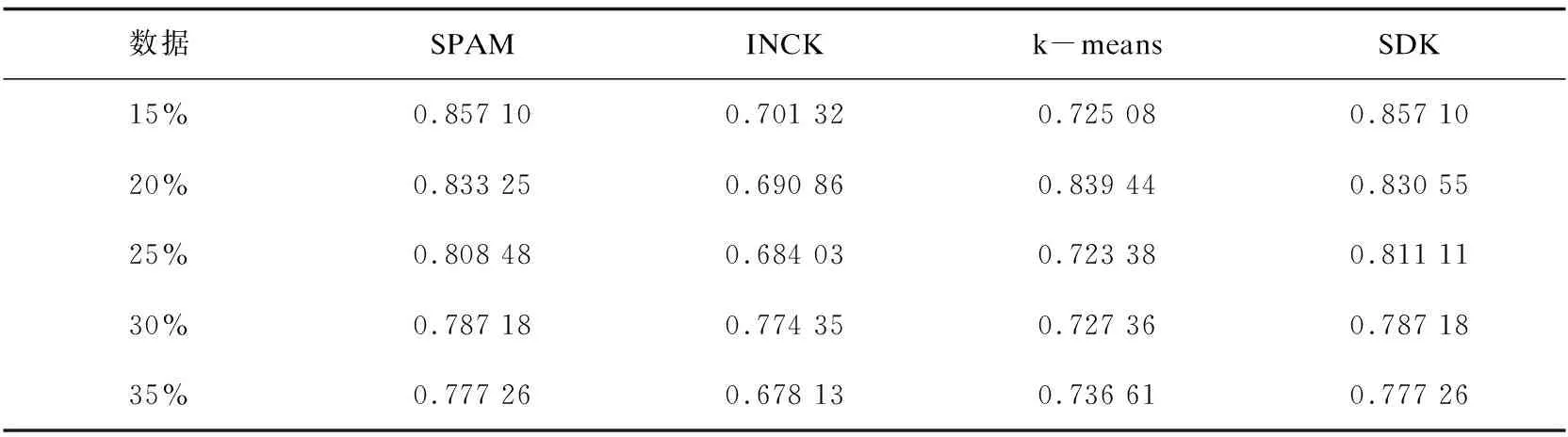
5 结束语
