一定要联立吗

福建省莆田第二中学 (351131)

蔡海涛

解析几何是高考数学的重要考查内容，直线与圆锥曲线位置关系又是解析几何中常见的重要考查类型.很多学生无法正确解答，往往是不知道设点的坐标还是直线方程，或是随便设一种形式，面对繁杂的运算最终难以完成.还有些教师甚至指导学生遇到直线与圆锥曲线位置关系时,就是“联立”、“判别式”、“韦达定理”的三部曲.笔者认为，设直线方程，与圆锥曲线方程联立,然后设而不求、整体代换,确实是常规套路,但是所有问题一定要联立吗？联立后又一定是整体代入吗？本文以近年来的高考题为例,谈谈这类问题处理的方法和策略.

1.大联立

(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB.

(2)当l与x轴重合时，∠OMA=∠OMB=0°.当l与轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB.

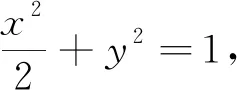
综上，∠OMA=∠OMB.

评注:直线与圆锥曲线位置关系问题，常常是先设直线方程，再把它与圆锥曲线方程联立，如果不好求交点坐标，一般是把已知条件或要解决问题进行坐标转化，利用韦达定理整体处理，用代数方法来解决几何问题.这种处理方法叫“大联立”，适合于交点坐标较难求出的类型.

2.小联立

(1)当t=4,|AM|=|AN|时，求△AMN的面积；

(2)当2|AM|=|AN|时，求k的取值范围．

评注:本题与例1类似之处是设直线,然后与圆锥曲线方程联立，区别之处是容易解出交点坐标.这种处理方法叫“小联立”，适合于知道一个交点坐标的情况，可根据韦达定理求出另一个交点坐标.往往这种类型已知一个点的横坐标为1,则可以利用韦达定理求出两根之积易得另一点坐标,或是已知一个点的横坐标为0,则可以利用韦达定理求出两根之和易得另一点坐标,一个点的纵坐标为1或0时情况类似.

3.不联立

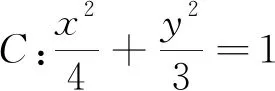
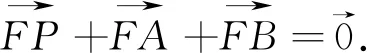
总之，以上三种方法是解决直线与圆锥曲线位置关系问题的常用方法，在具体应用时，应仔细分析，灵活选取.