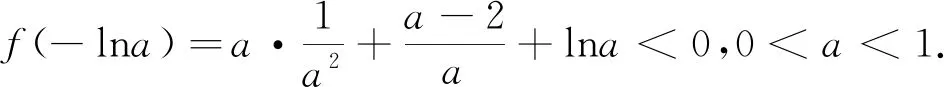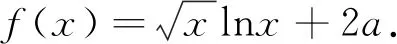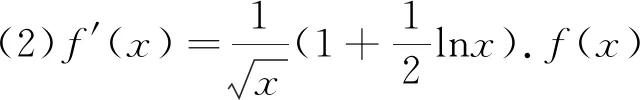例谈函数零点问题中的取点策略
2019-07-08浙江省绍兴市绍兴鲁迅中学312000
浙江省绍兴市绍兴鲁迅中学 (312000)
陈少春
近几年高考导数压轴题一个热点是考查函数零点(图像交点)个数问题,代数上判断无法求解零点的零点个数最常用的就是零点存在定理加单调性去处理,即若函数f(x)在区间[a,b]上是一条连续不断的曲线,且函数f(x)在(a,b)上单调,f(a)·f(b)<0,则函数f(x)在区间(a,b)上有唯一的零点.这个定理在应用时的难点是两个端点a,b的函数值符号的确定,很多学生谈“点”色变.下面笔者结合具体例子谈谈函数零点问题中取点策略,希望对考生备考有些许帮助.
一、直接取点
直接取点可以分成两类:常值取点和带参取点.不带参函数或者代常值能把参数消去很
多时候取具体值就可以解决问题,带参函数且不容易消参的往往要带参取点,这类问题的处理策略是利用这个点代入之后以参数为自变量的函数的单调性,代入这个点后把高次降成低次(三次降成二次,一次)转换成熟悉的函数再处理等等.
例1 设函数f(x)=ex-ax+a(a∈R)其图像与x轴交于A(x1,0),B(x2,0)两点,且x1 解:f′(x)=ex-a,f(x)在区间(-∞,lna)单调递减,(lna,+∞)单调递增.若f(x)与x轴有两个交点,则f(lna)=a-alna+a<0,a>e2.取x=1,f(1)=e-a+a=e>0;取x=a,f(a)=ea+a-a2>0.由零点存在定理知,在区间(1,lna),(lna,a)各存在一个唯一的零点.所以a的取值范围a>e2. 例2 (2019届浙江新高考联盟22)设a∈R,已知函数f(x)=xlnx+ax2-(1+a)x+1,x∈(1,+∞). (1)若f(x)>0恒成立,求a的取值范围; (2)证明:存在实数a使得f(x)有唯一零点. (1)若a=3,求f(x)的单调区间; (2)证明:f(x)只有一个零点. 综上,f(x)只有一个零点. (1)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8-8ln2; (2)若a≤3-4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点. 另一方面,由f(x)=kx+a得k= 例5 (2018年全国3理21)已知函数f(x)=(2+x+ax2)ln(1+x)-2x. (1)若a=0,证明:当-1 (2)若x=0是f(x)的极大值点,求a. (2)如果不等式(1+kx)f(x)>1+x对f(x)定义域内一切值都成立,求实数k的所有可能的值. 笔者发现很多模拟题往往是指对数函数放缩成幂函数,从而导致很多学生形而上学,机械操作,其实有些问题把幂函数往指对数函数转化能使问题得到更快更好的解决. 例7 (2017年全国卷1理21)已知函数f(x)=ae2x+(a-2)ex-x. (1)讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. (1)求f(x)的单调区间;(2)若f(x)有两个不同的零点,求a的取值范围.
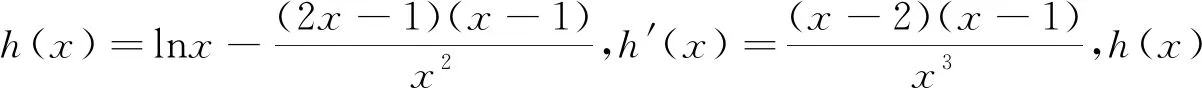
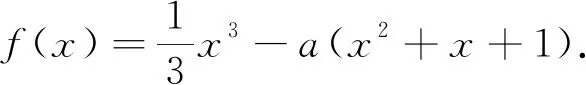

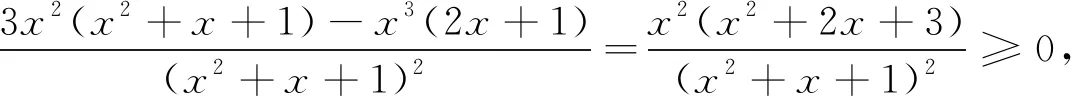
二、指对数放缩后取点
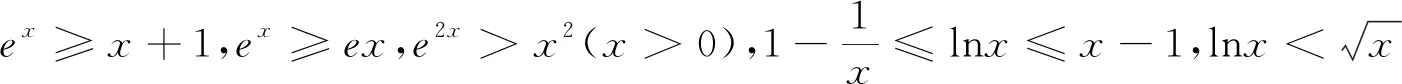
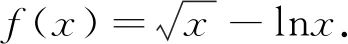
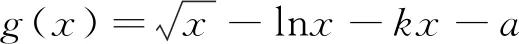

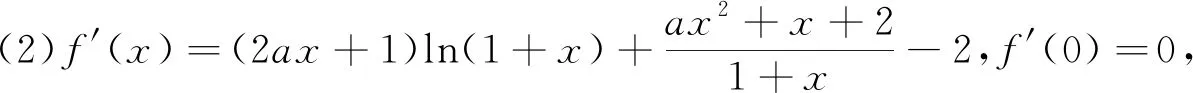
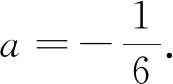


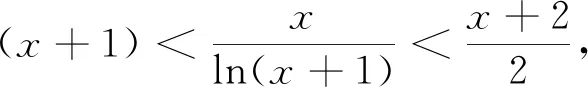

三、幂函数放缩后取点