也谈几类赛题的三角换元法

湖北省武昌实验中学 (430061)

彭 景

广东省珠海市实验中学 (519090)

王恒亮

三角换元法是解决高中数学问题的常用方法，合理利用此方法不仅能降低思维难度还能简化相关运算，它是高中生必须熟练掌握的几种方法之一.高中阶段的各级各类数学竞赛中都不乏有三角换元的影子，合理利用此法有时候可以给我们带来意想不到的效果，笔者结合自己的教学实际谈谈几类赛题中的三角换元，希望对读者有所帮助.

类型1x2+y2=A2>0,(x=Acosθ,y=Asinθ).

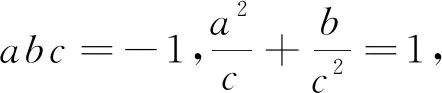
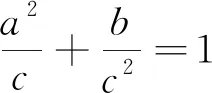
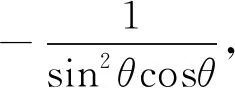
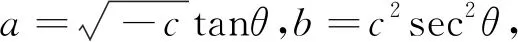
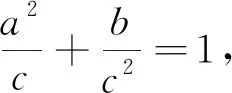
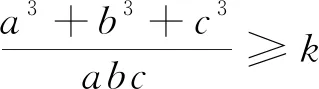
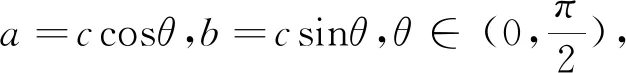
类型2x2+y2+z2=A>0,(x=Acosθcosφ,y=Acosθsinφ,z=Asinθ).

例3 (2010年湖北省高中数学联赛试题)

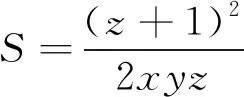
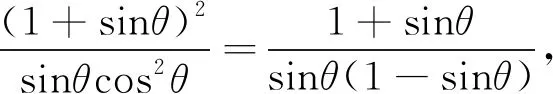
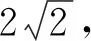
例4 (2009年浙江省高中数学竞赛试题)

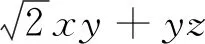
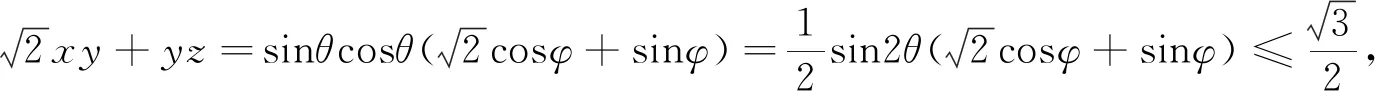
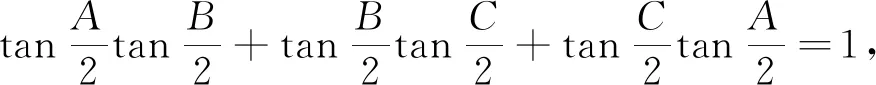
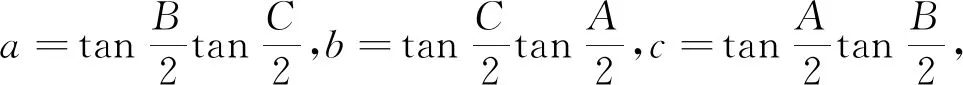
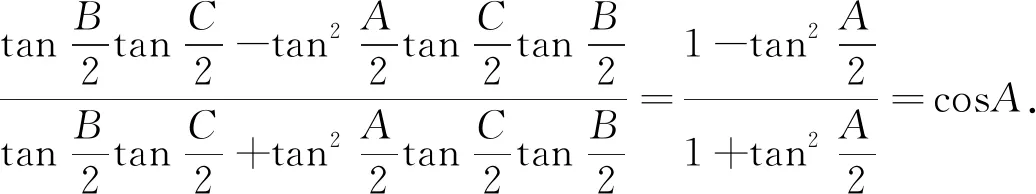
注：具备三角代换意识，对于条件a+b+c=1的快速转换将有助于分析问题、解决问题，本题的证法有多种，但用三角代换证法是其中比较简单的.

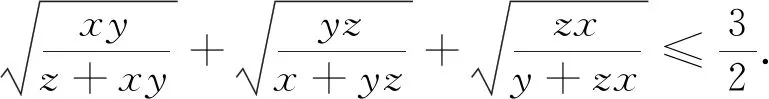
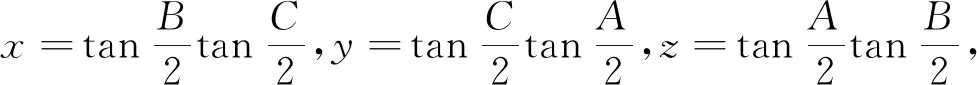
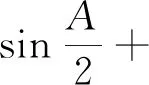
类型4x,y,z∈R+,x+y+z=xyz,(x=tanA,y=tanB,z=tanC).

在ΔABC中，有恒等式tanA+tanB+tanC=tanAtanBtanC，于是当遇到条件“x+y+z=xyz”时可以作作三角代换：x=tanA,y=tanB,z=tanC.

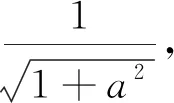
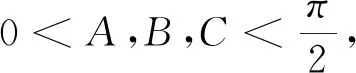
注：一般地，遇到条件a,b,c∈R+,a+b+c=abc,我们往往首选三角代换a=tanA,b=tanB,c=tanC,这种代换往往可以给我们带来很多意想不到的效果！

类型5x,y,z∈R+,xy+yz+zx=1,(x=cotA,y=cotB,z=cotC).

x=cotA,y=cotB,z=cotC.