例谈零点存在定理在导数及其应用中的作用*

福建省龙岩第一中学 (364000)

刘文娟 林文柱

由于导数在函数的图像、性质及其应用过程中所具有的基础性、工具性作用，以及在这一过程中对学生所应具有的将知识迁移到不同情境中的能力、逻辑推理能力及运算能力等方面有着较高的要求，近年来，导数及其应用问题已经成为高考的热点问题.考查的这部分内容在解题策略以及推理论证能力，理性思维的层次和深度等方面都有一定的要求，这就给中学数学教学在提炼和总结解题方法，扩大学生的知识视野，拓宽学生解决问题途径和思维途径，激发学生求新、求异等方面提出了更高的要求.

本文以高考复习中导数及其应用问题作为背景材料，把导数与函数的零点紧密联系起来，解决相关数学问题上其优越性就能表现出来.现将材料整理，与各位同仁交流.

一、例题呈现,思路探析

例1 ∃x0∈(2,+∞),k(x0-2)>x0(lnx0+1),则正整数k的最小值为．

(参考数据：ln2≈0.6931,ln3≈1.0986,ln5≈1.6094)

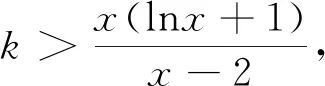
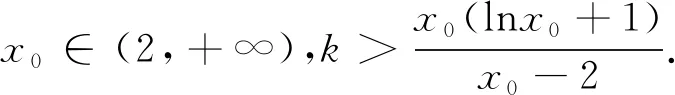
又H(8)=8-2ln8-4=4-6ln2<0,H(9)=9-2ln9-4=5-4ln3>0,故∃x0∈(8,9),使得H(x0)=x0-2lnx0-4=0.从而g(x)在(2,x0)上单调递减，在(x0,+∞)上单调递增.因此g(x)的最小值为g(x0).

变式1 已知函数f(x)=x+xlnx,若k∈Z,且k(x-1)1恒成立，则k的最大值为．

类比例题1，解答过程略.

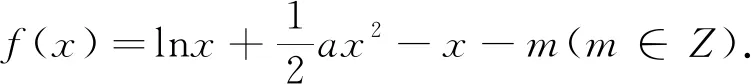
(1)略;(2)若a<0,且f(x)<0恒成立，求m的最小值．

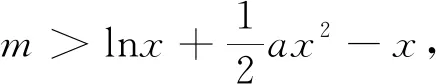
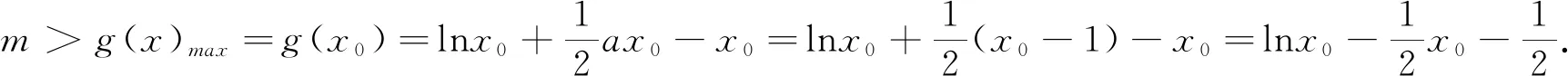
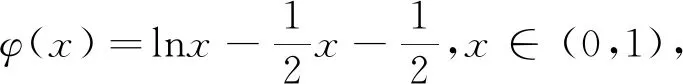
二、总结归纳，深度挖掘

通过上面两道例题的解答过程，我们可以分析得到在“恒成立”或“存在性”问题中求参数的最大(小)整数值的一般解答步骤：

1.分离参数，将问题转化为研究函数的最值问题；

2.对所整理的函数求导，当导函数值的符号不容易确定时，常常对导函数(导函数的部分函数)二次求导，利用零点存在定理，求出二阶导函数的驻点，从而判断原函数的单调性；

3.利用求导的方法可求出某一函数的最值，如果求出的最值仍然是含有变量的表达式，那么再确定这一表达式的最值时仍然需要求导.

上面的例题讲评后，笔者再布置了一道题作为课后练习:

练习已知函数f(x)=mx+2-ex(m∈R),其中e为自然对数的底数.

(1)略；(2)已知m=1,k为整数，若对任意的x>0，都有(k-x)f′(x)>-x-1恒成立，求k的最大值．

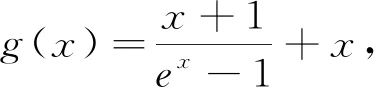
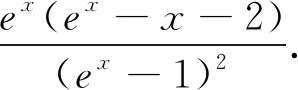
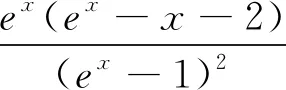
三、反思提升

把握问题本源，探究解法自然.罗增儒教授在《数学解题学引论》中指出：解答数学习题的实质是：“解数学题，这就是要找到一种一般数学原理(定义、公理、定理、定律、公式)的序列，把这些原理用于习题的条件或者条件的推论(解答的中间结果)，得到习题所要的东西，即习题的答案.”[1]

因此，在平时教学时，对一些有难度的题目，可以试着从学生的角度出发，帮助学生形成思考问题的切入点，提炼数学本质，形成自然流畅的解题方法，这样学生可以多题一解，提炼数学的通用方法.从而提升学生数学思维能力，摆脱枯燥乏味的题海战术.