平面向量中的最值问题及求解策略

广东省深圳市南头中学 (518052)

田彦武

最值问题，因为其题型的多样性，解决方法的灵活性和题目难度的综合性而受到高考的青睐，是高考考察的重点和热点问题．平面向量是高中数学教材中的新增内容，它的引入，不仅给高中数学教学带来了无限生机，而且给高考数学命题注入了新的活力，这是因为向量具有代数与几何形式的双重身份，它能将数学的很多知识联系起来，成为数学知识的一个交汇点．本文主要探讨平面向量中的最值问题，和大家共享．

1.向量模的最值问题

点评:本题利用向量模的定义及向量数量积的坐标运算，转化为关于t的二次函数来求模的最小值．

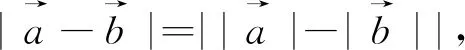
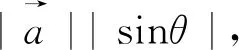
点评:本题的本质和例1类似，也转化为二次函数求解，但比例1稍微复杂一些而已，万变不离其宗！

2.向量数量积的最值问题

图1

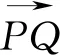
解法2:以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立直角坐标系．设|AB|=c，

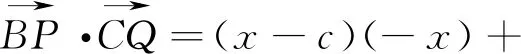
点评:本题两种解法各有千秋，方法1是利用向量的加减法运算法则将两向量的数量积转化为向量夹角的三角函数，然后利用三角函数的有界性解决最值；方法2是建立坐标系后将向量转化为坐标形式，后面和方法1一致．两向量的数量积是一个实数，故数量积的最值最终转化为函数的最值解决．

3.向量中参数的最值问题

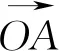
解：设∠AOC=α，

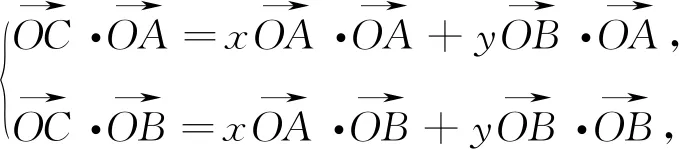
点评:本题根据平面向量基本定理，充分利用向量数量积的意义，将参数表示成向量夹角的三角函数，然后利用三角函数的性质求解最值．

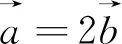
综上所述，平面向量中的最值，基本都可以转化为相关参数的函数，然后利用解决函数最值的方法来求相应的最值．