轨道参数对轮轨耦合系统固有频率的影响

马维国，关庆华，钟文生，陶功权，金学松，温泽峰

（西南交通大学 牵引动力国家重点实验室，成都610031）

铁路运输系统中，车辆系统和轨道系统是密不可分的两大组成部分，二者通过轮轨耦合组成一个相互作用的大系统。车辆在轨道上运行是一个轮轨相互作用的复杂动力学过程，影响因素众多，既有车辆方面的、也有轨道方面的，并且相互影响[1]。轨道作为铁路系统的重要组成部分之一，其固有特性对车辆运行平稳性、舒适性和安全性等有重要影响。因此，研究轨道参数对轨道系统特性的影响有重要意义。荆果等[2]通过力锤敲击试验研究了轨枕间距对钢轨振动的影响，其结果表明随着轨枕间距的增加，钢轨同阶模态频率会减小。和振兴等[3]研究了城市轨道交通轨枕间距对车辆轨道系统的动力学影响，研究表明，轨枕间距越大，车辆轨道系统的冲击响应越大。Wu 和Thompson[4]研究了随机轨枕间距和道床刚度对轨道振动的影响，认为轨枕间距和道床刚度随机变化引起的点响应和振动衰减是在一个范围内。Oscarsson[5]研究了轨垫刚度、道床刚度、轨枕间距对轨道振动的影响，分析了各参数对轮对垂向加速度、轨枕最大位移、轮轨最大接触力的影响。练松良和刘富[6]的研究表明P2力随轨道刚度的增大而增大，当轨道刚度较大时，P2 力的增大会对列车安全运行与轨道受力有不利影响。耿传智和吴觉波[7]运用模态分析理论研究了有砟轨道垂向振动特性，分析了轨道结构的固有振动特性及垫层刚度与阻尼的影响，并与落轴试验进行了对比。尚文军等[8]运用模态分析和有限元理论，研究了不同轨道支撑条件对钢轨固有频率和振型的影响。雷晓燕[9]将傅里叶变换应用于轨道结构动力分析中，研究了轨下胶垫、扣件刚度和阻尼、道床刚度和阻尼对轨道振动特性的影响。关庆华等[10]通过Laplace 变换法求解簧下质量-轨道系统的耦合振动频率和振型，分析了车辆和轨道系统的P2共振频率及参数影响规律。

关于轨道参数对轨道和车辆簧下质量耦合系统固有频率影响的研究较少，本文考虑整体道床参数和轨枕间距随机分布的影响，运用ANSYS软件分别建立了普通短轨枕整体道床轨道有限元模型和簧下质量轨道耦合系统有限元模型，通过模态分析和谐响应分析研究轨道参数对轨道和簧下质量轨道耦合系统固有频率的影响。

1 轨道现场测试与扣件刚度识别

为了获得轨道特性，对某地铁普通短轨枕整体道床轨道进行了力锤敲击试验，测试现场如图1所示。

图1 轨道力锤敲击测试现场照片

本次现场轨道敲击测试选用激励频带为0～2 000 Hz的铝制锤头进行测试。轨道响应信号由加速度传感器采集，现场测试分别在轨枕上方轨头和跨中轨头安装加速度传感器。为了减小测试误差，测试结果通过敲击5次取平均所得。

图2给出了轨枕上方和跨中钢轨垂向敲击垂向响应的频响特性，结果表明，在0～1 200 Hz范围内，存在204 Hz 和1 110 Hz 两个较为明显的振动峰值，其中，轨枕上方轨头和跨中轨头在204 Hz的轨道振动响应相似，该频率为钢轨的1 阶垂向弯曲频率。两位置处钢轨振动差异主要表现在1 110 Hz，这是扣件周期性离散支撑导致的振动频率，即Pinned-Pinned共振频率。Pinned-Pinned共振的波长等于两个轨枕间距，其驻波节点刚好在轨枕支撑处（扣件处），若以轨枕间距简支支撑的钢轨Euler 梁模型考虑，Pinned-Pinned共振频率计算可表示为[11]

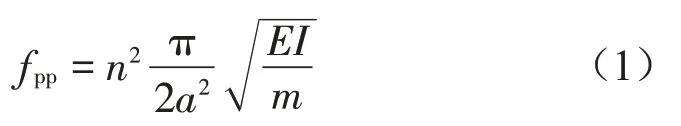
式中：n为钢轨Pinned-Pinned 振动阶数，a为轨枕间距（m），EI为钢轨垂向抗弯刚度（N·m2），m为单位长度钢轨的质量（kg/m）。由公式（1）可知，Pinned-Pinned 共振频率仅由钢轨类型和轨枕间距决定，当钢轨类型确定后，1 阶Pinned-Pinned 共振频率只与轨枕间距有关，随轨枕间距的增大而减小。

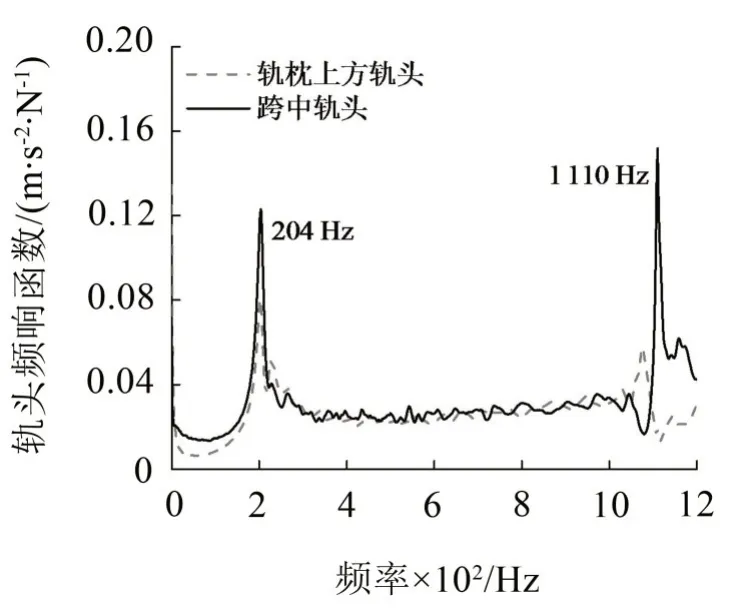
图2 普通短轨枕轨道结构垂向频响特性

为考虑车辆的作用，在车辆通过时，测量了车辆和轨道部件振动加速度。车辆运行速度约为62 km/h～75 km/h。图3给出了普通短轨枕3个不同区间轨道的轴箱振动加速频谱，在0～800 Hz 频率范围内，轴箱垂向振动加速度峰值所对应的频率为64 Hz。

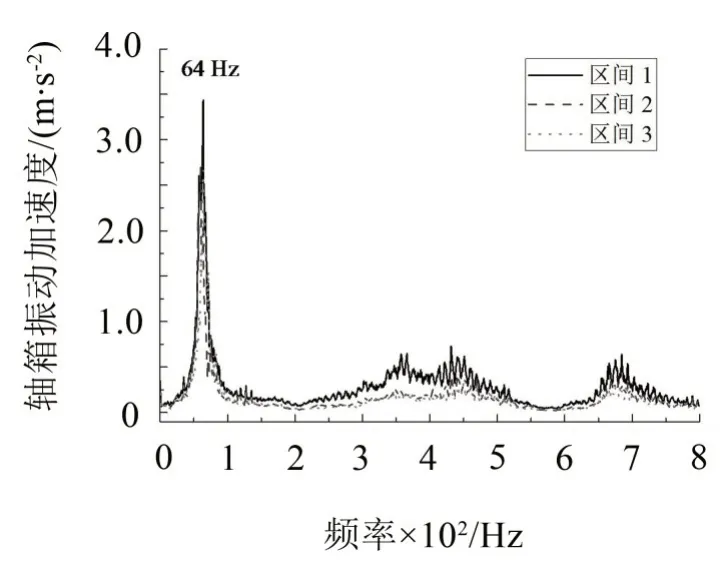
图3 车辆轴箱振动加速度频谱图

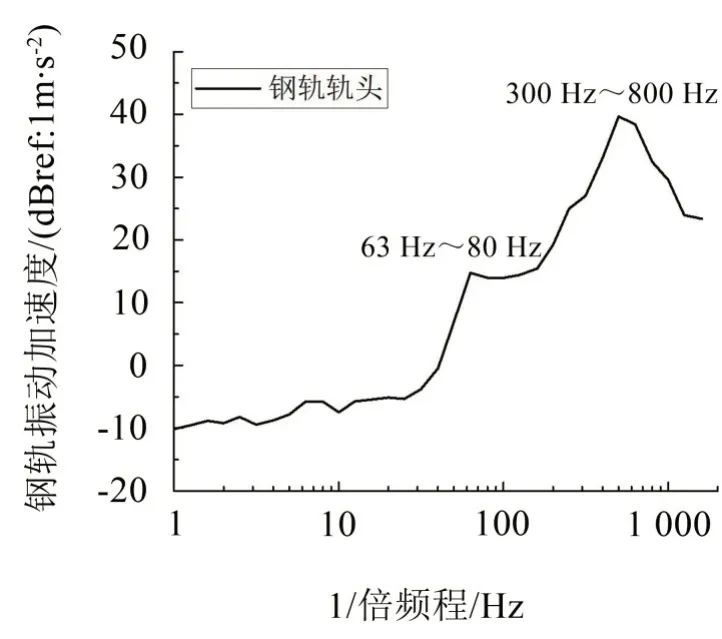
图4 钢轨振动加速度1/3倍频程图

图4给出了轨道振动加速度1/3倍频程图，可知在63 Hz～80 Hz 和300 Hz～800 Hz 处分别出现了峰值，且第一个峰值与车辆轴箱振动相重合，为车辆轨道系统的P2共振频率。第二个峰值是由31.5 mm短波钢轨波磨引起。Timoshenko于1926年通过无质量Winkler地基梁模型求得轨道垂向振动固有频率，可表示为wR=(k/m)0.5，其中，k为Winkler 地基弹性系数[10]。由力锤敲击测试可知，钢轨的1阶垂向弯曲频率为204 Hz，由k=m(2 πf)2反推钢轨基础弹性系数为9.86×107N/m2。根据K=ka（a为轨枕间距，K为扣件刚度）换算得扣件刚度为5.92×107N/m。

2 轨道特性仿真计算分析模型

2.1 数值模型

理论上，轨枕在纵向上基本以相等间距分布，故由钢轨和轨枕组成的轨道结构可近似认为是无限周期支撑结构，由于轨道响应的影响范围有限，在满足分析精度的情况下，通常以有限长模型来分析轨道振动[12]。试算表明，选取20 个枕跨的长度进行建模可以满足分析精度。普通短轨枕整体道床轨道主要由钢轨、扣件、短轨枕、混凝土道床板和地基组成。由于短轨枕镶嵌在道床板内并与其固结在一起，两者之间几乎没有缓冲减振特性，因此，建模时将扣件直接与道床板相连。

图5为利用有限元软件ANSYS 所建立的有限元模型，采用combin14弹簧阻尼单元模拟钢轨与道床板间的扣件弹性及道床板与地基之间的弹性联结。以beam188Timoshenko 梁单元模拟钢轨，钢轨两端施加固定约束；道床板用Solid185 实体单元模拟。由于轨道结构的对称性，本文选取轨道结构的一半进行计算。轨道板对称中面与两端均施加对称约束。

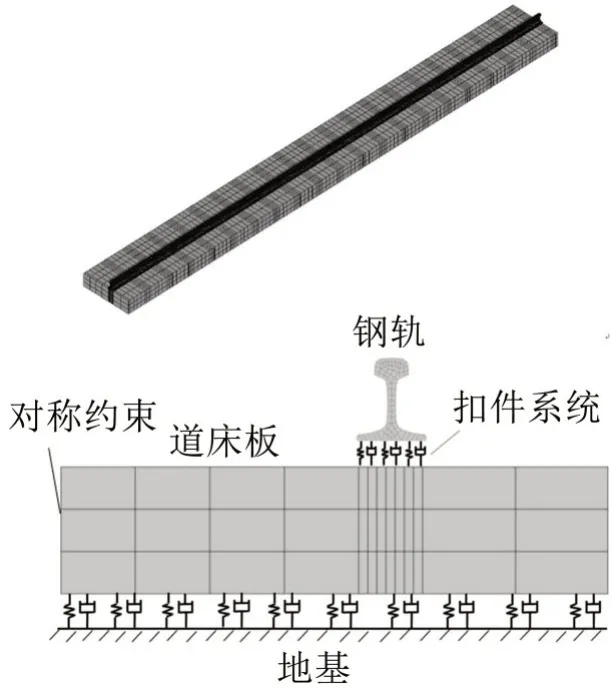
图5 整体道床轨道有限元模型

由于地基支撑刚度的变化对钢轨1阶垂向弯曲频率的影响不大（见下文），而扣件刚度对钢轨1 阶垂向弯曲频率的影响较大，可将钢轨基础弹性系数视为扣件离散支撑分布刚度。由文献[13]知，隧道内无砟轨道地基弹性系数取1 200 MPa/m。建模基本参数如表1所示。在下文的分析中，若不加说明，均采用表1中参数进行计算。

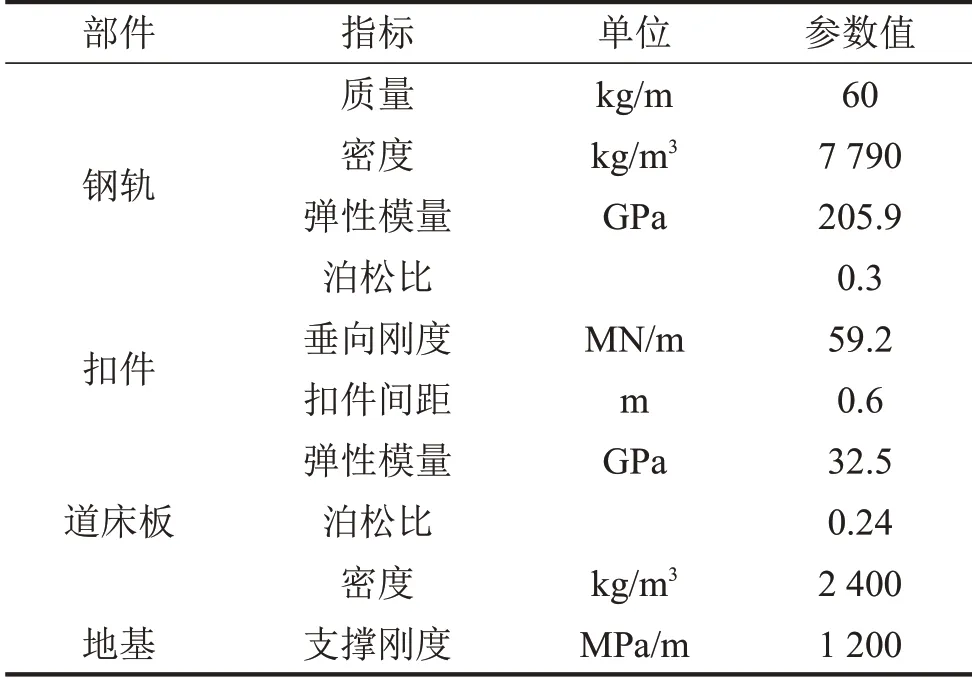
表1 轨道部件参数

2.2 谐响应分析

对轨道模型施加幅值为1 kN 的时变正弦载荷进行谐响应分析，分别计算跨中激励跨中响应和轨枕上方激励轨枕上方响应的位移导纳，结果如图6所示。

由图6可知，在0～1 200 Hz 范围内有2 个明显的响应峰值，对应频率分别为202 Hz和1 112 Hz，与力锤敲击结果基本一致。

2.3 模态分析

通过模态分析获得轨道结构的固有频率。其中钢轨1、2阶垂向弯曲频率及Pinned-Pinned共振频率随扣件刚度的变化曲线如图7所示。

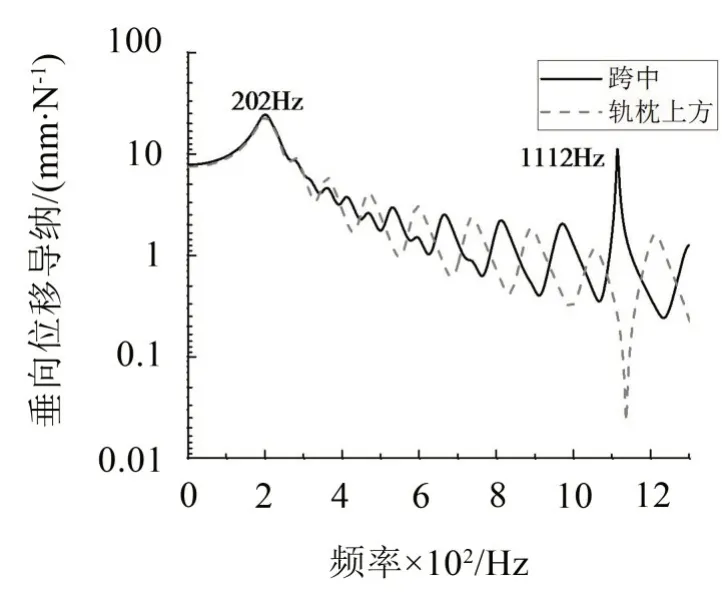
图6 轨道垂向位移导纳

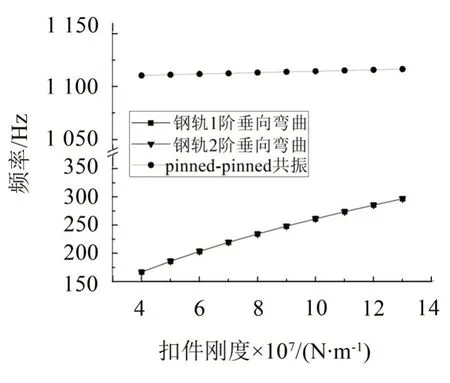
图7 轨道特征频率随扣件刚度的变化

图7结果表明，钢轨的1、2阶垂向弯曲频率基本相等，且随扣件刚度的增加而增加；Pinned-Pinned共振频率几乎不受扣件刚度变化的影响。图8给出了钢轨1、2阶垂向弯曲频率及Pinned-Pinned共振频率随地基刚度的变化曲线，显然，地基刚度的变化对这3个特征频率影响较小。

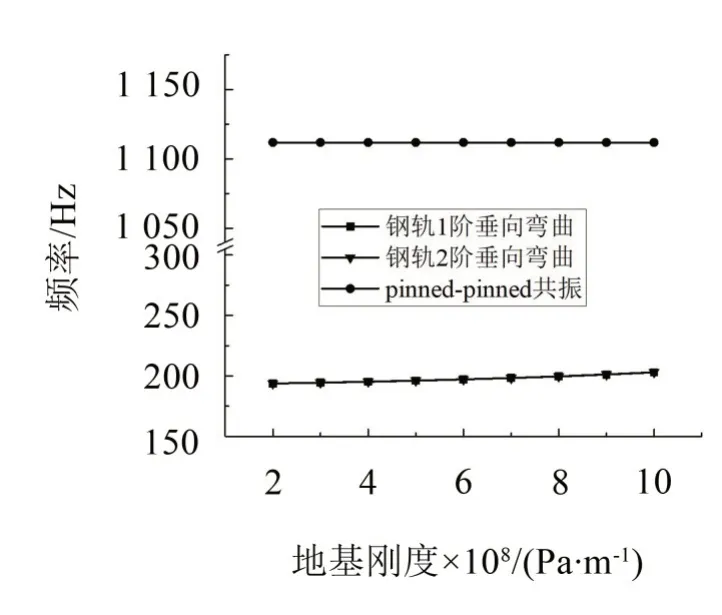
图8 轨道特征频率随地基刚度的变化

由于钢轨1阶垂向弯曲频率受扣件刚度影响较大，受地基支撑刚度的影响较小，故可以使用钢轨1阶垂向弯曲频率反推扣件刚度。

3 簧下质量轨道耦合模型及各参数对耦合系统振动特性的影响

P2 共振为簧下质量与轨道作为整体质量在轨道弹性基础上的振动。其1阶垂向弯曲频率即为P2共振频率。图9为簧下质量轨道耦合系统有限元模型，簧下质量取1 290 kg。

图9 簧下质量轨道耦合模型

轮轨之间的接触通过弹簧单元模拟，其接触刚度取1.524×109N/m[10]。有限元模型计算的P2 共振频率为63.1 Hz，与试验结果64 Hz基本一致。

3.1 扣件刚度的影响

扣件是钢轨与轨枕之间的联结件，它的作用是固定钢轨，阻止钢轨纵向和横向位移，并提供适当弹性减振隔振。根据地铁和轨道交通车辆轴重及减振的要求，扣件垂向刚度一般取值为10 kN/mm～40 kN/mm，但是，当线路运营一段时间后，轨道部件老化等原因会使得扣件垂向刚度变大，如本文测试的普通短轨枕整体道床轨道扣件垂向设计刚度为40 kN/mm，而通过力锤敲击反推的扣件垂向刚度却达到了59.2 kN/mm。图10为簧下质量轨道耦合系统P2共振频率和2阶垂向弯曲频率随扣件刚度变化曲线，随着扣件刚度增大，P2共振频率和系统2阶垂向弯曲频率明显增大，第2 阶垂向弯曲频率随扣件刚度的增长率要高于P2共振频率的增长率。

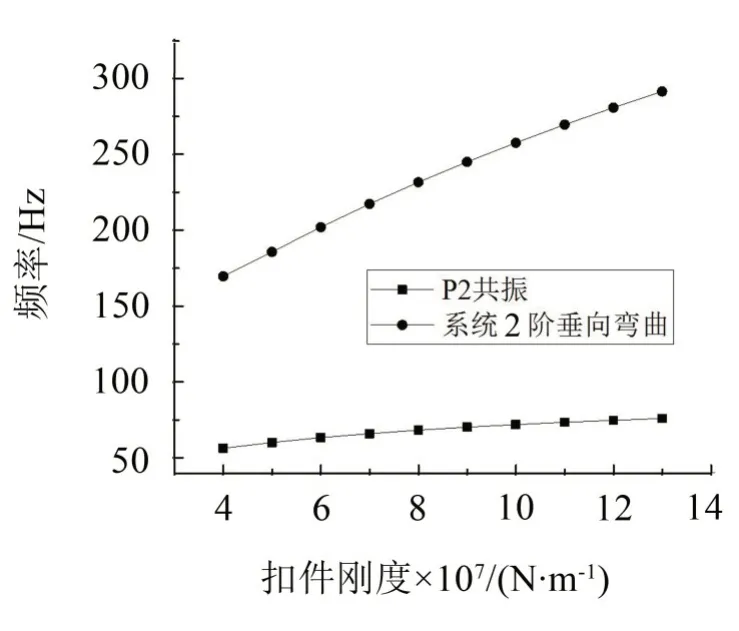
图10 系统前2阶固有频率随扣件刚度的变化

3.2 簧下质量的影响

图11为簧下质量轨道耦合系统P2 共振频率和2阶垂向弯曲频率随簧下质量变化曲线。

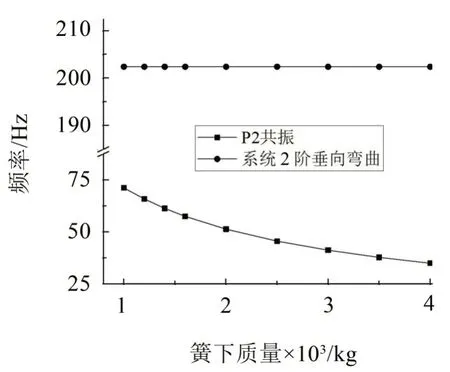
图11 系统前两阶固有频率随簧下质量的变化

可知，P2 共振频率随簧下质量的增大而减小，簧下质量对耦合系统2阶垂向弯频率的影响可以忽略；这是由于P2共振为簧下质量和轨道质量在轨道基础上同相振动，而轨道参振质量远低于簧下质量，故簧下质量对P2共振频率的影响较为明显，而系统2阶垂向弯曲频率实际上是由轨道固有特性决定，因此，簧下质量对系统2 阶垂向弯曲频率的影响可忽略。这与文献[10]的计算结果相一致。

3.3 地基支撑刚度的影响

由文献[13]知，无砟轨道位于土质路基上时，地基刚度一般取85 MPa/m；无砟轨道位于桥梁上时，地基刚度取1 000 MPa/m；无砟轨道位于隧道内时，地基刚度取1 200 MPa/m。图12为簧下质量轨道耦合系统P2共振频率和2阶垂向弯曲频率随地基刚度变化曲线。

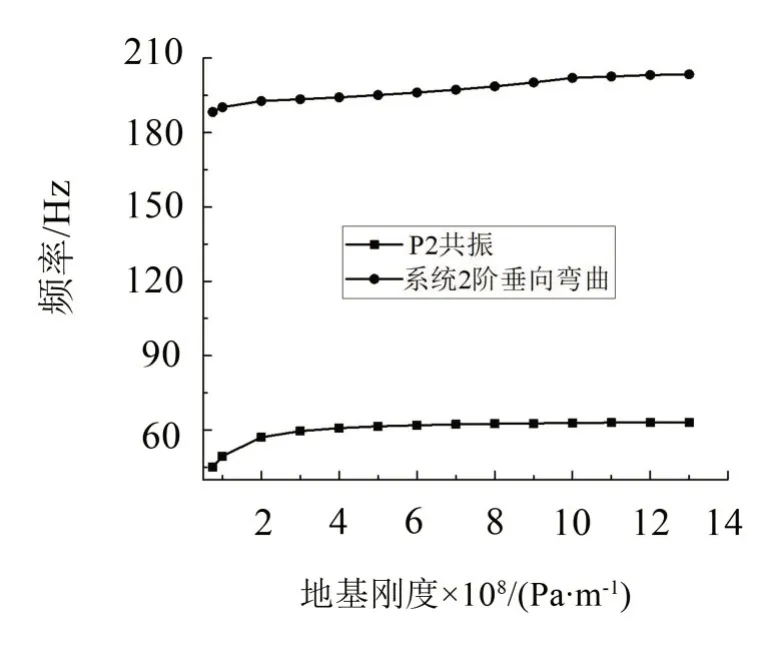
图12 系统前两阶固有频率随地基刚度的变化

P2共振频率随地基刚度的增大而增大，当地基刚度大于300 MPa，地基刚度的变化对P2 共振频率影响较小。地基刚度对耦合系统2阶垂向弯曲频率的影响较小，因此，下文分析中假定地基刚度不变。

3.4 轨枕间距的影响

轨枕间距与每公里配置的轨枕根数有关，而轨枕的根数是由运量、行车速度及线路条件确定，以求在最经济的条件下，保证轨道具有足够的强度和稳定性。同时，不当的轨枕间距设置易诱发钢轨波磨，在车辆通过时产生剧烈的振动和噪声，加剧轨道和车辆部件的疲劳破坏。为研究轨枕间距对轨道特性的影响，在0.5 m～0.7 m 范围对不同轨枕间距轨道系统的1 阶垂向弯曲频率、Pinned-Pinned 共振频率以及簧下质量轨道耦合系统的P2 共振频率进行了计算。结果如图13所示。

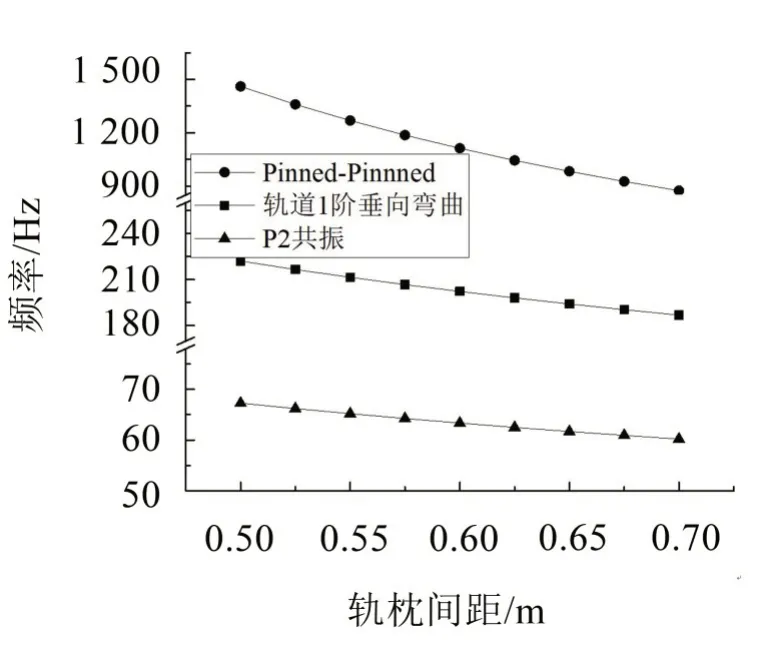
图13 轨枕间距对轨道特性的影响

从图13可知，Pinned-Pinned共振频率、轨道1阶垂向弯曲频率及耦合系统P2 共振频率随轨枕间距的增大而减小。

相同扣件刚度和相同钢轨基础分布刚度时取0.5 m、0.6 m轨枕间距计算轨道系统1、2阶垂向弯曲频率及簧下质量轨道耦合系统的P2共振频率，如表2所示，表中结果表明，钢轨基础分布刚度不变的情况下，轨枕间距的变化对1、2 阶垂向弯曲频率及簧下质量轨道耦合系统的P2 共振频率影响较小。若扣件刚度相同，轨枕间距增大将导致钢轨基础分布刚度下降，使得系统各频率有所下降。

3.5 随机轨枕间距的影响

在理论分析中，我们通常将轨枕间距看作是均匀分布的，然而实际上，由于轨道在建造时安装精度的限制以及运营中轮轨相互作用、轨道维修，轨道状态发生变化，轨枕间距并不是一个定值，而是在一定范围内变化。因此，有必要研究轨枕间距在一定范围内随机分布对轨道振动特性的影响。在有限元模型中考虑中间10 组轨枕间距的随机分布，使用MATLAB 中rad 函数生成10 个在0.5～0.7 范围内分布的随机数组作为轨枕间距。左右两端的5跨使用均匀的0.6 m 的轨枕间距，共进行了10 个随机工况的计算，结果如图14所示。

图14中横轴为不同轨枕间距的情况，0.6表示轨枕间距为0.6 m 均匀分布情况，s1～s10 表示10 种随机轨枕间距的分布。可知，轨道1、2 阶垂向弯曲频率波动较小，Pinned-Pinned 共振频率波动较大。轨枕间距随机分布的10 种情况中，轨道1 阶垂向弯曲频率最大差值为5.6 Hz，2阶垂向弯曲频率最大差值为6.8 Hz，Pinned-Pinned 共振频率最大差值为64 Hz，P2 共振频率最大差值为2.2 Hz。最大差值与相0.6 m 等间距情况下各频率的比率分别为2.8 %、3.3%、5.7%、3.4%。由各频率最大差值占相应等间距频率的百分比可知，轨枕间距随机分布对这几个频率影响较小。

表2 扣件刚度与各频率的关系

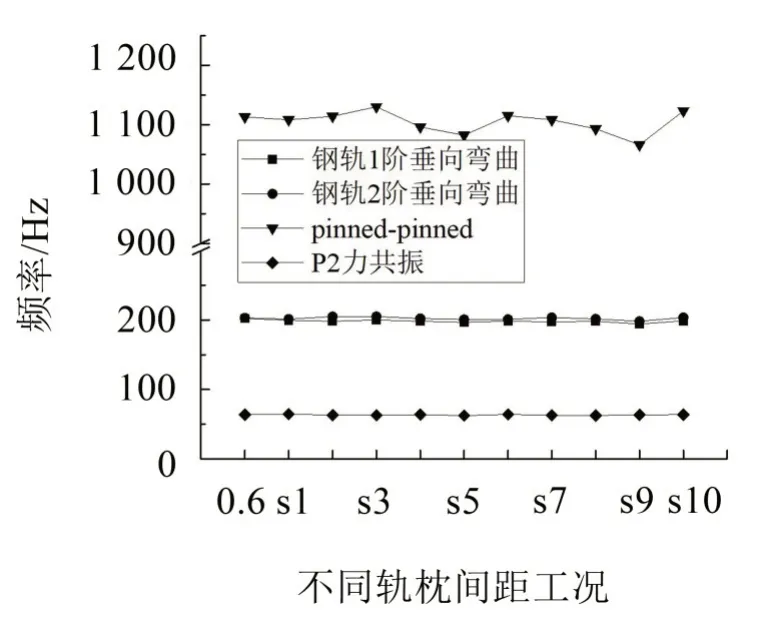
图14 随机轨枕间距对轨道特性的影响

对轨枕间距随机分布轨道结构进行谐响应分析，钢轨垂向位移导纳计算结果见图15。

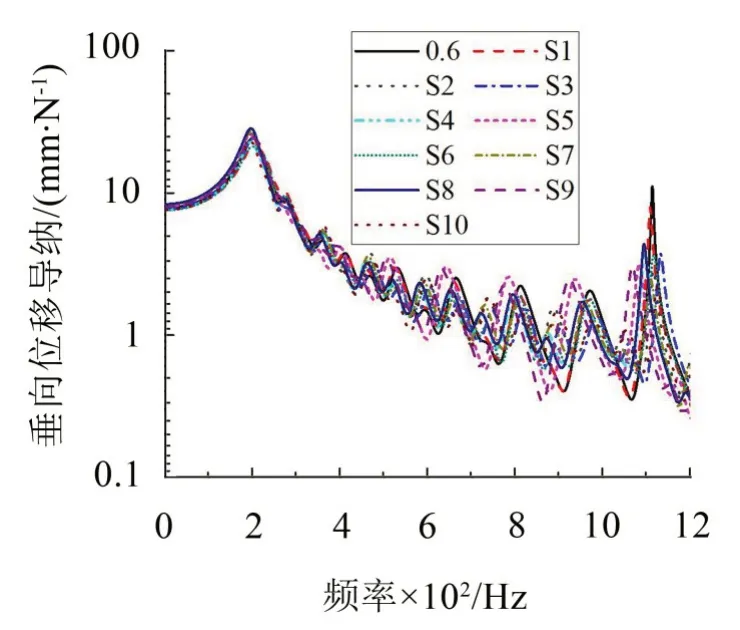
图15 随机轨枕间距的轨道垂向位移导纳

由图15可知，在0～1 300 Hz 范围内，轨枕间距随机分布对轨道垂向位移导纳均有影响。在Pinned-Pinned 共振频率处，等间距轨道响应峰值最大，这是因为轨枕间距均匀时，Pinned-Pinned共振波长为2 个轨跨的长度，反射波在激励点处以相同的相位叠加，所以Pinned-Pinned 共振的响应峰值较大，当轨枕间距随机分布时，反射波具有相位差，因此，Pinned-Pinned共振的响应峰值有所下降，与文献[4]结果一致。在计算的10 种随机轨枕间距分布情况中，Pinned-Pinned 共振的响应峰值为均匀分布时的19.7%～71.8%。

在其它频率处响应峰值随机变化，可能大于也可能小于等间距轨枕的轨道响应。这是因为轨枕间距随机变化时，激励点处的平均刚度也是随机变化的。

4 结语

结合现场力锤敲击测试与车辆轨道振动测试，利用有限元模型分析了轨道参数对轨道系统及簧下质量轨道耦合系统动态特性的影响，得到以下结论：

（1）轨道1 阶垂向弯曲频率随扣件刚度的增大轨道1阶垂向弯曲频率的影响较小，故可由钢轨1阶垂向弯曲频率反推扣件刚度。P2 共振频率随扣件刚度的增大而增大，随簧下质量的增大而减小，当地基刚度小于300 MPa/m 时，P2 共振频率随地基刚度的增大而增大，当地基刚度大于300 MPa/m时，地基刚度的变化对P2共振频率的影响较小。

（2）轨枕间距均匀分布时，相同扣件刚度和地基刚度条件下，轨道1 阶垂向弯曲频率、Pinned-Pinned 共振频率及耦合系统P2 共振频率随轨枕间距的增大而减小。

（3）轨枕间距随机分布时，相同扣件刚度和地基刚度条件下，轨道1、2 阶垂向弯曲频率、Pinned-Pinned 共振频率及耦合系统P2 共振频率均有所波动，Pinned-Pinned共振频率最大差值为64 Hz，相对于等间距Pinned-Pinned 共振频率的变化比率为5.75 %。轨枕间距随机分布对0～1 300 Hz 范围频率的响应幅值均有影响。轨枕间距随机分布可有效降低Pinned-Pinned共振的响应峰值，在计算的10种情况中，可降至均匀分布时的19.7%～71.8%。