复合式流体滤波器的衰减性能分析

罗先聪，周知进,2，古莹奎，熊 雄

(1.江西理工大学 机电工程学院，江西 赣州341000；2.贵州理工学院 机械工程学院，贵阳550003；3.西南科技大学 制造科学与工程学院，四川 绵阳621010)

随着液压系统逐渐朝高压、大功率、高速方向发展，容积式液压泵的排油机制产生了流量脉动，流量脉动产生压力脉动，压力脉动对系统产生不利影响，严重时对系统产生巨大破坏作用，造成生命和财产损失。因此，研究液压系统中的压力脉动衰减机理成为国内外专家关注的重点[1-2]。目前采用主动式和被动式来衰减液压系统中的压力脉动，主动式脉动衰减器是通过引入与初级脉动源幅值相等，相位相反的脉动，以达到衰减的目的。由于主动式难控制，可靠性差，成本高等原因。目前还处于研究阶段[3-4]。

被动式是采用合理的衰减结构，设置合理的结构参数，具有结构简单，成本低，衰减效果良好等优点。现在主要有赫姆霍兹衰减器[5]，旁路谐振器[6]等。但是都存在滤波频率窄，频率选择性强的特点，在低频段具有较好的衰减效果。

国内外专家学者设计了各式各样的流体滤波器，曹秉刚等利用电液比拟的方法，分别对H型和K型滤波器进行研究，数值模拟表明，H 型和K 型都能在一定频域内有效衰减压力脉动，但是实验研究显示，K型比H 型的滤波效果还要好些[7-8]。1998年，竹下等发明专利是在T 型分支管内部加上多处以上的节流口，把衰减器分为多腔室，通过调节滤波器结构参数改变共振频率，可以衰减多个频率范围的压力脉动[9-10]。窦雨淋[11]利用流体网络建模方法，提出一种改进的H 型流体脉动衰减器，数值模拟表明，在理想负载情况下，该衰减器对低频衰减效果较好。盖晓玲等[12]基于微穿孔板吸声理论和H型共振理论，提出一种镶嵌亥姆霍兹共振器的微穿孔板吸声体，数值仿真显示，低频吸声峰值由亥姆霍兹主导，高频共振峰与微穿孔板相关，达到了宽频的效果。焦生杰等[13]研究了H 型液压滤波器各参数对滤波效果的影响。仿真和试验表明，在液压系统中，共振频率处的系统阻抗达到局部最小，当颈径和颈长适中时，体积越大，阻抗越小，滤波效果越好。官长斌等[14]利用集中参数法，对3自由度的H型衰减器，提出一种旋转矢量优化方法，该方法的目的是搜索谐振器未知的结构参数，使谐振器的共振频率与液压泵的流体脉动谐波一致，优化结果表明该方法的可行性，并且在模拟的最佳结构参数下，表明集中参数法与传递矩阵法的具有相同的精度。

虽然基于H 型的各种衰减滤波器已经有大量的研究，但是对H型与K型的复合式流体滤波器研究甚少，H型和K型滤波器分别对低频和高频的压力脉动滤波效果较佳。为此，本文结合各自的滤波特点，利用电液比拟的方法，建立复合式流体滤波器的等效电路图，分析复合式流体滤波器对压力脉动的衰减性能。

1 复合式流体滤波器工作原理

复合式流体滤波器结构示意图如图1所示，主要以K型和H型滤波器串联组成，当液压泵的流量脉动遇到系统阻抗时产生压力脉动，压力波传到复合式流体滤波器时，遇到截面积突变，一部分压力波进入复合式流体滤波器，另一部分沿管道继续前进，进入滤波器的部分压力脉动分别在直径为d1的容腔与d2、d3的小孔中，并且在小孔中会产生液柱，液柱在压力脉动的作用下像活塞一样做往复运动。同时，液体产生的液柱有一定的粘性和质量，在管道阻尼的作用下，消耗了压力脉动产生的能量。K 型部分和H 型部分的容腔有阻碍压力脉动变化的特性，当与压力波谐振频率与滤波器固有频率一致时，便产生共振。此时，对压力脉动的衰减达到最佳。

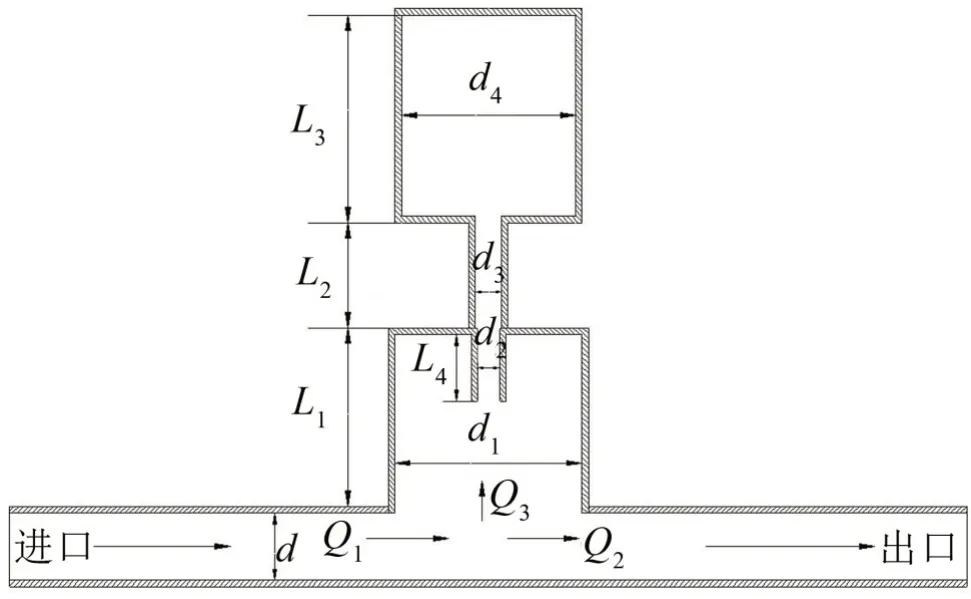
图1 复合式流体滤波器结构示意图

2 复合式流体滤波器的数学模型

在实际工作中，由于流体滤波器需要接入液压系统，在滤波器的后面会加装负载，负载对滤波器的衰减特性会产生很大的影响。因此，以如图2液压系统建立流体滤波器的数学模型。其中，A1，B1，C11为直管道，T1为衰减器，负载端采用“直管道+节流阀”。P2、Q2分别为安装滤波器后压力和流量。

图2 脉动衰减器液压系统模型

由图2脉动衰减器液压系统模型，基于电液比拟的方法，可以建立的等效数学模型如图3所示。

图3 脉动衰减器液压系统模型等效电路图

其中，Z1是液压泵与流体滤波器一段直管道的阻抗，Z2为流体滤波器与压力测量点之间管道的阻抗，Z3是衰减器的阻抗，分别由K型和H型滤波器引起的流阻R1、R2，流感L11、L12，流容C1、C2组成的，ZL为“直管道+节流阀”的负载阻抗，P1、Q1和P2、Q2分别为液压泵输出的压力和流量和“直管道+节流阀”前面的压力和流量，Q3为分支流量。

从文献[11]中得出管道阻抗为

式中：d为管道直径，为油液的密度，μ为油液的动力粘度，s=j×w，w为角频率，LA,LB分别为A1、B1管道的长度。

由流体力学[15]知其中为压强波的传播速度，Ke为油液的体积模量。即阻抗Z3可以表示为

其中：

在线性电路理论中，图3为带有负载无源T型四端网络，由节点定律和回路定律可得

经过计算可得

对于A1、B1、C11直管道的传递矩阵为

由于液压管道C11较长，为了减小计算误差，C11管道段需要用分布参数法计算。设节流阀的阻抗为，其中：ΔpT为节流阀的压差，qT为通过节流阀的流量。则有

即：

评价滤波器的衰减性能一般采用传递损失和插入损失，传递损失反映滤波器的本身的传递特性，取决于滤波器的结构尺寸和介质特性，不受负载和液压源的影响。插入损失不仅与滤波器的本身特性有关，而且还受液压源，负载特性的影响。因此，本文采用插入损失评价滤波器的衰减性能。取d′点位置的压力进行计算，一般由流体网络的传输方程P2(s)=Q2(s)·ZL，由(4)式可得P1(s)与P2(s)的关系。

即：

由(4)和(7)式得

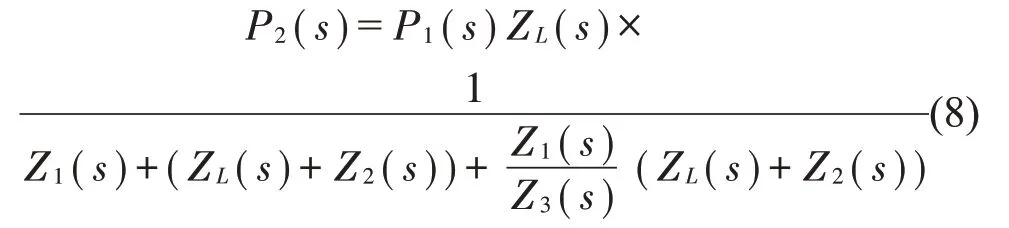
若没有加装流体滤波器时，即Z3=∞，则有

由插入计算公式有

式中：P′2为没有加装流体滤波器前的压力脉动；P2为加装流体滤波器后的压力脉动。

3 复合式流体滤波器的衰减性能分析

图4为复合式流体滤波器插入损失仿真曲线。从图中可以看出，流体滤波器在频率为331 Hz出现峰值点。在高频部分810 Hz以上，插入损失分贝数出现增长趋势。仿真显示：低频部分由H 型部分主导，高频部分与K型部分相关。

图5分别比较了”K+H”型，“H+H”，”H”型滤波器的衰减压力脉动情况，仿真表明，在相同部分具有相同的参数情况下，“K+H”在低频部分的共振频率点与“H+H”，“H”的共振频率接近，尤其与“H+H”最为接近。但是“H+H”型出现了2个峰值，分别为284 Hz 和659 Hz。从图5可以看出，在频率为972 Hz～2 000 Hz 区间，复合式流体滤波器的衰减效果都要好于“H”与“H+H”型。说明了“K+H”型衰减器对高低频压力脉动具有较好的衰减能力，实现了“H”型滤波器对低频与“K”型滤波器对高频的各自衰减频段的特点，结构比“H+H”型结构更紧凑，高频部分衰减效果更好。复合式流体滤波器对压力脉动衰减在低频部分的共振频率点与单个“H”型并不重合，主要原因是复合式流体滤波器“H”型部分与“K”型部分的内插管串联，造成复合式流体滤波器“H”型部分的共振频率点降低。

表1 仿真基本参数

图4 复合式流体滤波器插入损失仿真曲线

图5 3种滤波器的滤波效果比较图

在表1中其他参数不变的情况下，仅改变K 型部分的d2直径，从图6可以看出，增加d2的值，曲线向右移动，高频部分的曲线基本不变，主要原因是K型部分的内插管与H 型部分串联，影响了曲线在低频部分的固有频率点。

图6 K型部分的d2直径对插入损失的影响

在表1中其他参数不变的情况下，仅改变K 型部分的容腔体积，图7给出了增加容腔直径d1，结果显示，随着d1直径的增加，高频部分的曲线向左移动，高频部分的衰减频率范围变宽。主要原因是增加K型部分的容腔体积。

图7 K型部分d1长度对插入损失的影响

在表1中其他参数不变的情况下，仅改变K 型部分的L4内插管的长度，图8给出了增加L4的长度，曲线在低频部分的固有频率点向左移。

图8 K型部分L4长度对插入损失的影响

图9 液压直管道C11的Lc长度对插入损失的影响

在表1中其他参数不变的情况下，仅改变“液压直管道C11+节流阀”中直管道LC的长度，从图9可以看出，在高频部分，虽然曲线呈交错变换，衰减效果差别较小，但是通过局部放大图知，在模拟的频率范围内，增加LC的长度，在频率约为1 200 Hz～1 800 Hz区间时，插入损失增加逐渐放缓，当LC=0.5 m、LC=0.6 m与LC=0.4 m时相比较，插入损失出现较大的下降。综合以上分析，说明在加装滤波器时，在实际情况允许下，应尽量将滤波器适当靠近负载。以便获得最佳衰减效果。

4 结语

结合K 型和H 型滤波器的各自滤波特点，利用电液比拟的方法，建立液压系统等效电液图，对复合式流体滤波器的衰减效果进行分析，经过数值仿真，得出以下结论：

(1)提出一种以K 型和H 型滤波器串联的复合式流体滤波器，分别结合各自的滤波特点，有效拓宽了滤波器在高低频的滤波范围。结合实际工况，合理地选择结构参数，可以实现最佳的滤波效果。

(2)从图9可以看出，改变液压直管道C11的LC长度，会影响插入损失的大小和滤波范围，但是影响效果不显著，结合衰减器对高频的衰减效果综合情况来看，在加装滤波器时，在实际工况允许的情况下，应适当靠近负载，衰减的效果较好。复合式流体滤波器与串联的“H+H”型相比较，在高频部分滤波效果更好，在相同的参数下，结构更紧凑。

(3)改变K 型部分的直径d2和L4的值会影响低频部分的共振频率点，增加K型部分容腔直径d1，高频部分曲线向左移，拓宽了滤波器对高频段的滤波范围。