风电齿轮箱高速轴圆锥滚子轴承动态特性分析

沈意平，徐默然，唐斌龙，李 卉

(湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭411201)

风电齿轮箱是双馈风电机组中连接叶轮和发电机的重要部件，是传递能量和承受风载的核心部件。根据美国[1]和欧洲[2-3]相关研究机构统计资料表明：齿轮箱是风电机组故障率最高的部件之一，其引起的故障停机时间最长，其中约达50%源于高速轴轴承故障。高速轴输入端常采用圆柱滚子轴承，输出端采用圆锥滚子轴承，由于外部风载激励和内部激励，特别是齿轮箱输出轴与发电机轴不对中，将使高速轴轴承载荷增大，给轴承带来附加位移和动载响应，加速高速轴轴承过早失效[4-8]。根据ISO281轴承寿命计算公式，如果当量动载增大5%，其寿命将降低约15%。因此，为了保证齿轮箱长寿命、高可靠性的使用要求，需要深入研究高速轴轴承载荷变化对其振动响应特性的影响。

美国国家可再生能源实验室Keller[9-10]等通过理论计算、实验和现场测试对齿轮箱高速轴端轴承的载荷分布情况进行了较全面的研究。Bruce[11]等针对NREL 750 kW风电机组齿轮箱，采用多体动力学分析方法研究工作和停机条件下轴承的最大接触应力。秦大同[12]考虑齿轮和轴承的时变刚度，建立了齿轮箱平移-扭矩耦合动力学模型，研究随机风载下关键齿轮和轴承的可靠性。Sakaguchi[13]等采用ADAMS软件开展了圆锥滚子轴承保持架的运动特性，并与实验结果进行对比验证。Jiang 采用Simpack软件进行行星轮轴承载荷分析，轴承接触力采用面积分与有限元结合的方法计算。朱利军等采用ADAMS软件进行深沟球轴承钢球与内外圈和保持架之间的碰撞力等性能分析。

论文以某750 kW 风电齿轮箱高速轴输出端圆锥滚子轴承为分析对象，根据风电齿轮箱结构和风载工况分析圆锥滚子轴承轴向和径向载荷，采用ADAMS 软件建立圆锥滚子多体动力学模型，基于美国Spectra Quest转子实验台开展圆锥滚子轴承振动响应特性实验研究，通过理论、仿真与实验研究轴向和径向载荷变化对其动态接触力和振动响应特性的影响，将为风电齿轮箱高速轴圆锥滚子轴承选型与齿轮箱设计提供理论依据。

1 风电齿轮箱高速轴轴承载荷分析

某750kW风电机组齿轮箱采用一级行星轮系+两级定轴轮系组成，其传动比为1:67，其结构如图1所示。高速轴输出端圆锥滚子轴承由内圈、外圈、滚子和保持架组成，能够承受较大的轴向和径向载荷联合作用。根据额定工况下高速级齿轮啮合力与轴承布置位置计算得到圆锥滚子轴承的载荷，其径向载荷Fr为13 215 N，轴向载荷Fa为18 820 N。

图1 某750 kW风电齿轮箱结构图

然而由于外部随机风载、传动链轴系不对中等因素作用，圆锥滚子轴承载荷将偏离理论设计值，造成轴承振动响应发生变化。考虑圆锥滚子轴承高速旋转运动的离心力Fe，滚子受力分析如图2(a)所示，滚子与内、外滚道和挡板的接触载荷分别为Qi、Qe和Qf，接触角分别为αi、αe和αf，根据滚子的力平衡方程可得出

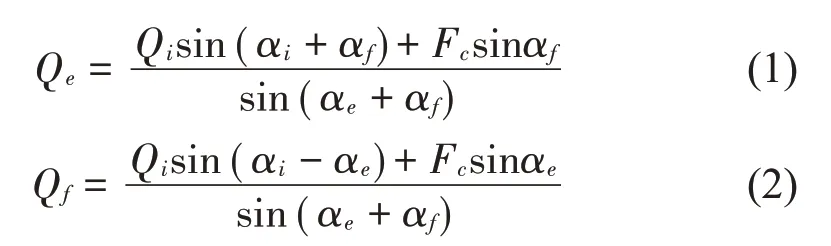
离心力Fc的计算式为

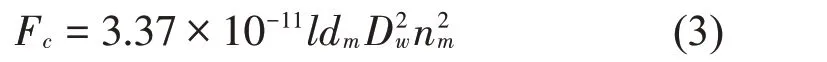
式中：l为滚子长度，dm为轴承节圆直径，Dw为滚子平均直径，nm为滚子公转速度。

对于单列圆锥滚子轴承，径向和轴向载荷联合作用下轴承同外圈将保持平行，并且分别产生相对位移δa和δr，如图2(b)所示，以最大载荷滚子为起点的任意角度位置ψ处的滚子载荷Qψ可写为

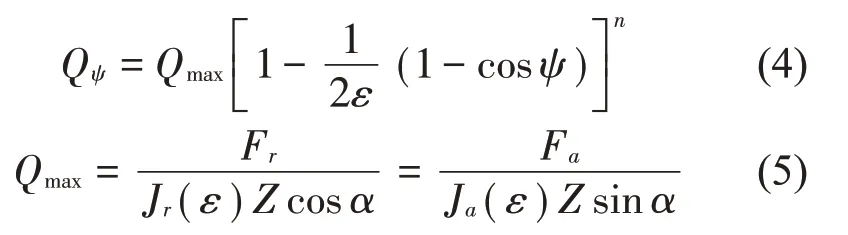
式中：ε为载荷分布系数，Jr(ε)为径向载荷积分，Ja(ε)为轴向载荷积分，α为载荷作用下实际的接触角，Z为滚子数目，滚子轴承中n通常取1.11。

根据Frtanα Fa通过查表可以获得圆锥滚子轴承滚子载荷计算所需的ε、Jr(ε)和Ja(ε)，进一步分析径向和轴向载荷作用下滚子接触载荷情况。

2 圆锥滚子轴承多体动力学模型

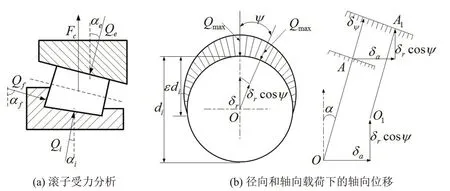
图2 圆锥滚子轴承载荷分析示意图

运转工况下圆锥滚子轴承各零部件之间复杂的接触碰撞使得其动力学特性异常复杂，论文采用多体动力学软件ADAMS 来分析其动力学特性。以750 kW风电齿轮箱的高速轴圆锥滚子为分析对象，其内径为d为110 mm，外径D为200 mm，宽度B为53 mm，滚子直径Dw为22 mm，滚子数目Z为16 个，内外锥角分别为11°和15°。该轴承内外圈和滚子材料为钢，密度为7 801 kg/m3，弹性模量为207 GPa，泊松比0.29；保持架为黄铜，密度为8 545 kg/m3，弹性模量为106 GPa，泊松比0.32。采用CATIA 软件建立圆锥滚子轴承的内圈、滚子、保持架和外圈模型并装配，其三维模型见图3所示。

图3 圆锥滚子轴承CATIA三维模型

将圆锥滚子轴承三维实体模型通过无缝接口软件SimDesigner导入ADAMS软件，根据各零部件间的运动关系，轴承外圈定义为固定副，滚子与内外圈为旋转副，外圈为固定副，内圈与外圈为方向副（即两轴线平行），保持架为平面副。滚子轴承运转过程中，考虑油膜润滑时，滚子与滚道接触形成弹性流体润滑油膜，因此，滚子与内外圈的接触刚度包括Hertz 接触刚度和油膜刚度两部分组成。滚子与内圈接触刚度为[13]

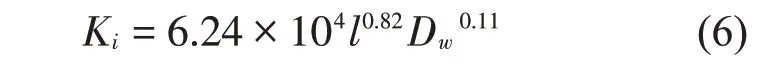
滚子与外圈接触刚度为

圆锥滚子轴承润滑油膜厚度直接影响着接触副的动力学特性，根据Grubin方程可知，两个钢制圆柱体最小油膜厚度可写为

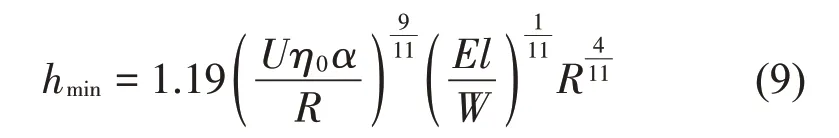
利用接触载荷对最小油膜厚度的微分来近似表达滚子轴承的油膜刚度

式中：W为单位长度滚子上的载荷；η0为油在常压下的动力黏度；U为无量纲速度参数；ζ为黏压系数；R为滚子与滚道间的等效半径。

圆锥滚子轴承中滚子与内外圈的等效接触刚度可写为

根据圆锥滚子轴承相应的参数，计算得到滚子与内圈接触刚度为1.54×105N/mm，滚子与外圈接触刚度为1.86×105N/mm。圆锥滚子轴承各零部件间的接触载荷采用ADAMS软件中的Impact接触力函数计算

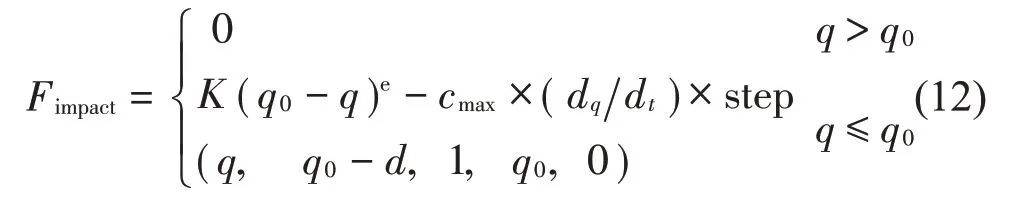
式中：q0为两物体产生碰撞的初始距离，q为两物体的实际距离，dqdt为两物体相对速度，K为接触刚度，即滚子与内外圈的接触刚度K∗i和K∗e，e 为力指数，cmax为最大阻尼系数，d为切入深度，它决定了何时阻尼力达到最大，step函数形式为

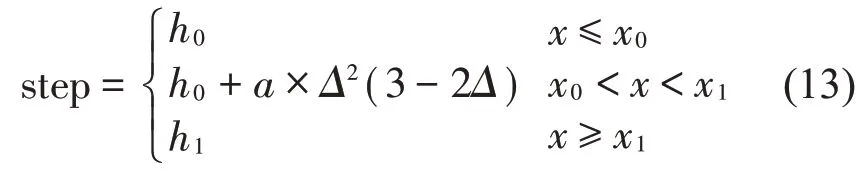
式中：a=h1-h0，Δ= (x-x0)(x1-x0)。

碰撞指数e 选为1.5，最大阻尼系数取内外接触刚度的0.1%，切入深度d取0.1 mm。ADAMS 中采用Coulomb模型计算摩擦力，其计算式为

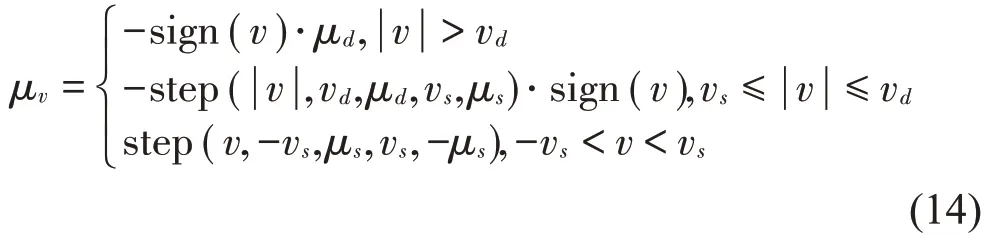
式中：vs为静临界速度，μs为静摩擦系数，vd为动临界速度，μd为动摩擦系数，分别取值为vs=100、μs=0.01、vd=1 000和μd=0.007。

为了保证ADAMS求解精度，本文采用SI2积分格式，积分误差设置为0.001。在ADAMS 中完成上述模型设置、运动副与约束设置、碰触接触参数设置和求解器设置，建立起圆锥滚子轴承多体接触动力学仿真分析模型。

3 圆锥滚子轴承动态响应分析

圆锥滚子轴承的载荷分布系数ε描述了受载区的大小和载荷分布的均匀程度，轴向载荷越大则ε越大。为了掌握不同轴向载荷作用下圆锥滚子轴承的最大接触力情况，假定额定径向载荷不变，分析ε分别为0.3，0.5，0.6，1 和1.25 5 种情况下轴承接触载荷情况，通过查表获得Frtanα Fa值，从而可以计算对应的轴向载荷分别为3 495 N，3 877 N，4 110 N，5 876 N 和8 554 N。圆锥滚子轴承的额定转速n=1 500 r/min，仿真模型时长0.5 s，仿真步数为4 000，仿真分析了不同载荷分布系数下圆锥滚子轴承振动响应情况。图4是ε为0.3时轴承滚子与内外圈接触力及受载滚子数目情况。图5(b)中引出直线表示该滚子受载，此时受载滚子数为6。图5是ε为0 时圆锥滚子轴承的轴心轨迹图。

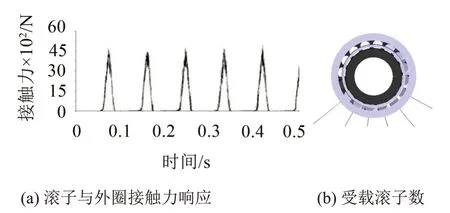
图4 ε=0.3时滚子与外圈接触力及受载滚子情况

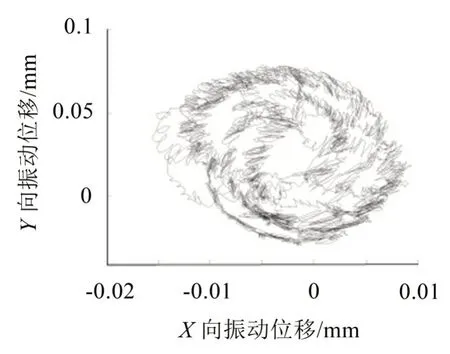
图5 ε=0圆锥滚子轴承的轴心轨迹图

采用理论计算圆锥滚子轴承最大接触力与ADAMS 仿真分析得到的接触力进行对比，相应的结果见表1。

表1 不同载荷分布系数下滚子与外圈的最大接触力

从表1可以看出：

(1)ADAMS仿真分析得到的不同载荷分布系数ε下受载滚子数目与理论分析得到的数目一致，同时仿真得到的滚子与外圈的最大接触载荷与理论分析结果误差均小10%，这说明了论文建立圆锥滚子轴承多体动力学模型的正确性，ADAMS 动力学仿真分析得到的接触力为动态接触力，更加符合实际运转情况。

(2)随着载荷分布系数的增大，轴向载荷相应增加，滚子与外圈间的接触力先随着受载滚子数量的增多而减小，当滚子全部受载后则随着载荷分布系数的增大而增加。

4 实验研究

基于美国Spectra Quest 转子实验台，开展了圆锥滚子动态特性实验，采用的圆锥滚子轴承型号为3021，径向载荷通过给轴承座顶部的螺栓施加预紧力来进行模型，如图6所示，3 个单方向加速度传感器安装于实验轴承座顶部和侧面，测试方向为2 个径向和1个轴向，采用丹麦B＆K公司开发的PULSE Labshop采集系统进行轴承振动信号采集，采用后处理分析软件Reflex对数据进行分析处理。采集时长20 s，采样频率为16.4 kHz。

图6 圆锥滚子动态特性实验装置

通过力矩扳手控制施加给径向加载装置的螺栓预紧力，开展了等效径向载荷为200 N、600 N、1 000 N、1 400 N和1 800 N等情况下的圆锥滚子轴承振动响应，图7所示为径向载荷为200 N时径向方向的加速度响应信号，各工况下的加速度均方根值汇总于表2，可以看出随着径向载荷增大，振动响应随着增大。

图7 径向载荷200 N时径向方向的加速度信号

表2 不同径向载荷下轴承振动值

5 结语

论文以某750 kW 风电齿轮箱高速轴圆锥滚子轴承为分析对象，基于ADAMS 软件建立了轴承的多体接触动力学仿真模型，分析了轴向和径向载荷变化下轴承动态接触力与振动响应特性。ADAMS软件仿真与理论计算得到的不同载荷分布系数下轴承最大接触应力与受载滚子数目结果一致，说明了建立多体接触动力学模型的准确性，阐明了轴向载荷增大将使滚子与外圈最大接触力的先减小再增大的变化规律，获得了不同径向和轴向载荷作用下轴承的振动响应，通过实验研究了径向载荷增大引起轴承振动响应加剧的变化规律。分析结果可为风电齿轮箱圆锥滚子轴承的动态设计和轴承寿命预测提供基础数据，将为风电齿轮箱轴承选型设计提供理论依据。