轨枕空吊动态演变规律
2019-05-09周和超包泽宇张树艺
周和超, 包泽宇, 张树艺
(同济大学 铁道与城市轨道交通研究院, 上海 201804)
随着高速铁路以及重载运输的发展,列车的运行速度和牵引质量不断提高,轮轨系统中的各种振动加剧,列车对轨道结构的破坏作用以及对线路变形的影响逐渐增大.由于钢轨表面不平顺造成的轮轨冲击力等原因,道床容易发生不均匀沉降,车辆长期通过后,道床沉降量不断地累积,造成轨枕与道床之间的接触面变小甚至完全消失,即轨枕发生部分或完全悬空.与此同时,由于轨枕无法正常地将来自钢轨的作用力传递至道床,因此容易导致轨枕破坏、钢轨扣件断裂等,加大线路维修成本,情况严重时甚至会引发列车脱轨的重大事故.为此,国内外相关学者针对轨枕空吊问题开展了一系列的研究.Dahlberg等[1]提出了混凝土轨枕的建模方法.Auguestin等[2]根据线路调查发现,目前大约有50%左右的轨枕存在程度各异的空吊现象.Olsson等[3]指出,在轨枕和道床间普遍存在着各种程度的空吊间隙.Kaewunruen等[4]对空吊轨枕的自由振动进行了详细分析.Grassie[5]在通过线路试验和数值计算对存在轨枕空吊的轨道动力学响应进行研究后指出,空吊轨枕将导致相邻轨枕承受的列车载荷增大,加快轨道恶化的速率.Ishida等[6]研究了轨枕空吊对轨道部件损坏的影响.肖新标等[7]建立了车辆-轨道耦合系统动力学模型,并分析了轨下支承失效对直线轨道动态响应的影响.张健等[8]比较了单根轨枕空吊面积对轨道动力响应的影响.邹春华等[9-10]通过搭建有砟轨道模型,提出了由路基不均匀沉降引起的轨枕临界空吊的计算方法.向俊等[11]通过数值仿真方法分析了轨枕空吊对车辆和轨道的影响.张大伟等[12]在对重载铁路轨枕空吊动力响应进行研究后指出,轨道不平顺与轨枕空吊叠加会加剧轮轨动力作用.然而,上述研究主要侧重于轨枕空吊形成后对车辆-轨道耦合系统动态响应的影响,对于轨枕空吊的形成过程则涉及较少.为此,本文建立车辆-轨道耦合系统动力学模型,结合道床沉降理论并通过多次迭代计算来研究轨枕局部空吊的演变过程,为线路维护提供理论指导.
1 计算模型
1.1 车辆-轨道耦合系统动力学模型
车辆-轨道耦合系统动力学模型主要包括车辆子系统和轨道子系统,两个子系统之间的相互作用通过轮轨接触关系来实现(见图1).本文中建立的货车模型共有39个自由度(见表1),采用传统的三大件式转向架.该转向架构架由左右两个独立侧架和一个摇枕组成,一系中央悬挂包括弹簧装置和摩擦楔块减振器,轴箱悬挂采用导框式定位.为使计算结果更为合理,建模时尽可能地考虑了系统的非线性环节,如轴箱干摩擦、楔块摩擦和三大件结构的抗菱形刚度等.对于轨道子系统,钢轨被视为连续弹性离散点支承上的Timoshenko梁,而轨下基础沿纵向以各轨枕支点为单元离散.由于轨道模拟长度超过100 m时足以满足计算精度的要求[13],因此本文中建立的轨道子系统长120 m.车辆-轨道耦合系统动力学模型的计算参数如表2所示.
1.2 轨枕空吊模型
正常情况下,轨枕与道床之间处于紧密贴合.由于车辆行驶、雨水冲刷等因素的影响,轨枕与道床之间产生分离,当轨枕与道床的接触面积减小或消失,轨枕即发生部分或完全悬空(见图2).为了研究轨枕局部空吊,选取任意一根轨枕将其近似简化为Timoshenko梁,并将其离散为10等份,通过弹簧-阻尼单元与轨枕下方的道床连接(见图3),具体计算参数如表3所示.图4显示的是如图3所示柔性轨枕的前5阶垂向弯曲模态,与之相对应的振动频率如表4所示.通过与相关文献对比可以发现,本文中采用的简化柔性轨枕模型具备较好的计算精度.在此基础上,针对该柔性轨枕出现的局部空吊现象,采用如图5所示的非线性函数来模拟轨枕与道床的接触状态,即轨枕空吊区域在车辆载荷的作用下向下自由运动,直到空吊间隙消失后与道床接触,道床产生一定的支承力.
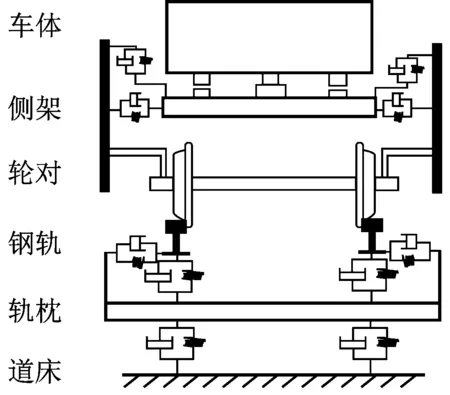
a 车辆-轨道耦合系统

b 动力学计算模型

部件部件具有该方向自由度纵向横向浮沉侧滚摇头点头车体√√√√√摇枕√侧架√√√轮对√√√√√

表2 车辆-轨道耦合系统动力学模型参数

图2 轨枕空吊示意图
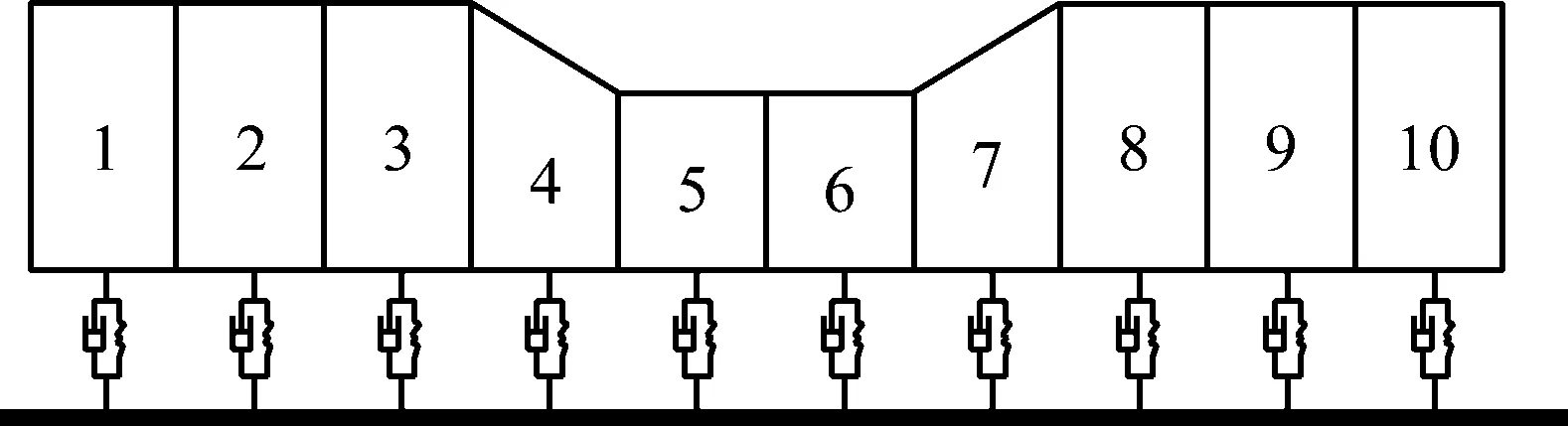
图3 柔性轨枕示意图
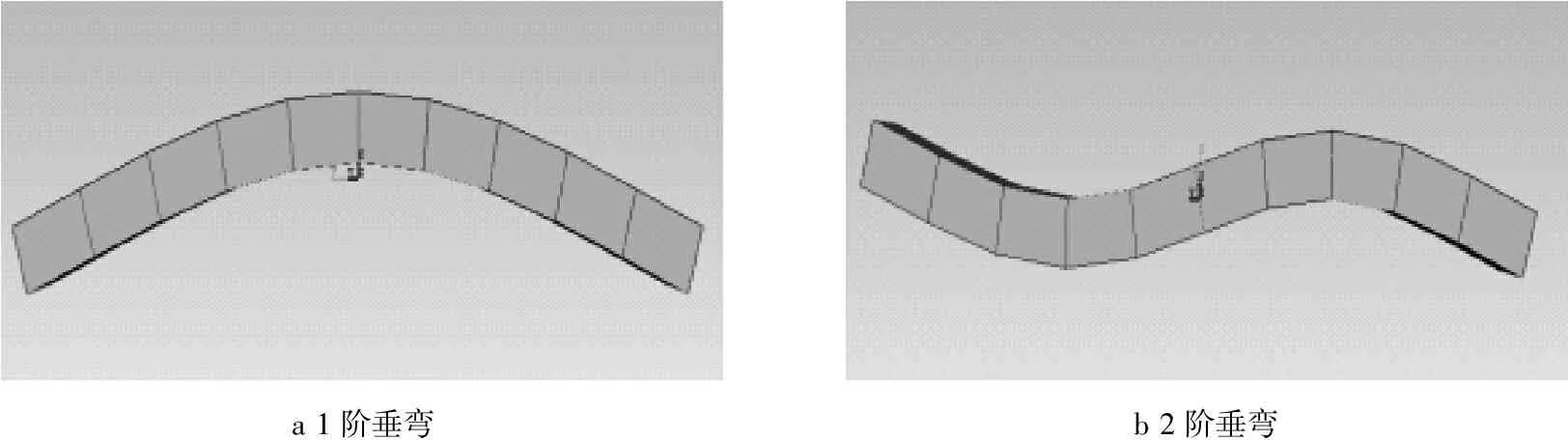
a 1阶垂弯b 2阶垂弯

c 3阶垂弯d 4阶垂弯
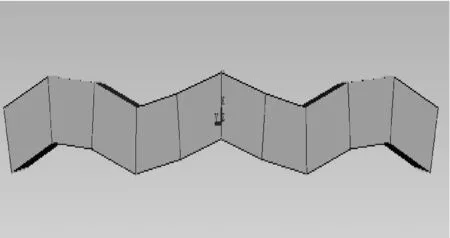
e 5阶垂弯

表3 柔性轨枕参数

表4 轨枕模态频率
1.3 道床沉降模型
道床在车辆载荷的累积作用下逐渐发生沉降,将道床在车辆载荷累积作用下的沉降全部视为轨枕的空吊间隙.此外,采用由Hettler[14]提出的道床沉降模型,如下所示:
uN=sF1.6(1+clnN)
(1)
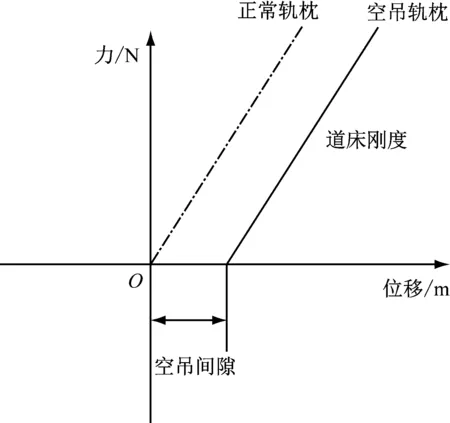
图5 轨枕-道床接触曲线
式中:uN是道床沉降;F是施加在道床上的车辆载荷;N是循环次数;s是比例因子,s=0.000 95;c是自然沉降常数,c=0.43.
1.4 计算流程
针对最为常见的两种轨枕空吊现象进行研究(见图6),并设置初始空吊间隙为3 mm.完整的计算流程如图7所示.首先设定轨枕局部初始空吊间隙,并利用车辆-轨道耦合系统动力学模型计算车辆通过时轨枕和道床的动力学响应.假设在一定的循环周期内车辆-轨道耦合系统不发生改变,从而结合道床沉降模型计算出新的轨枕空吊间隙,进而不断循环直至轨枕空吊程度不再发生明显变化.

a 轨枕单侧空吊

b 轨枕中部空吊
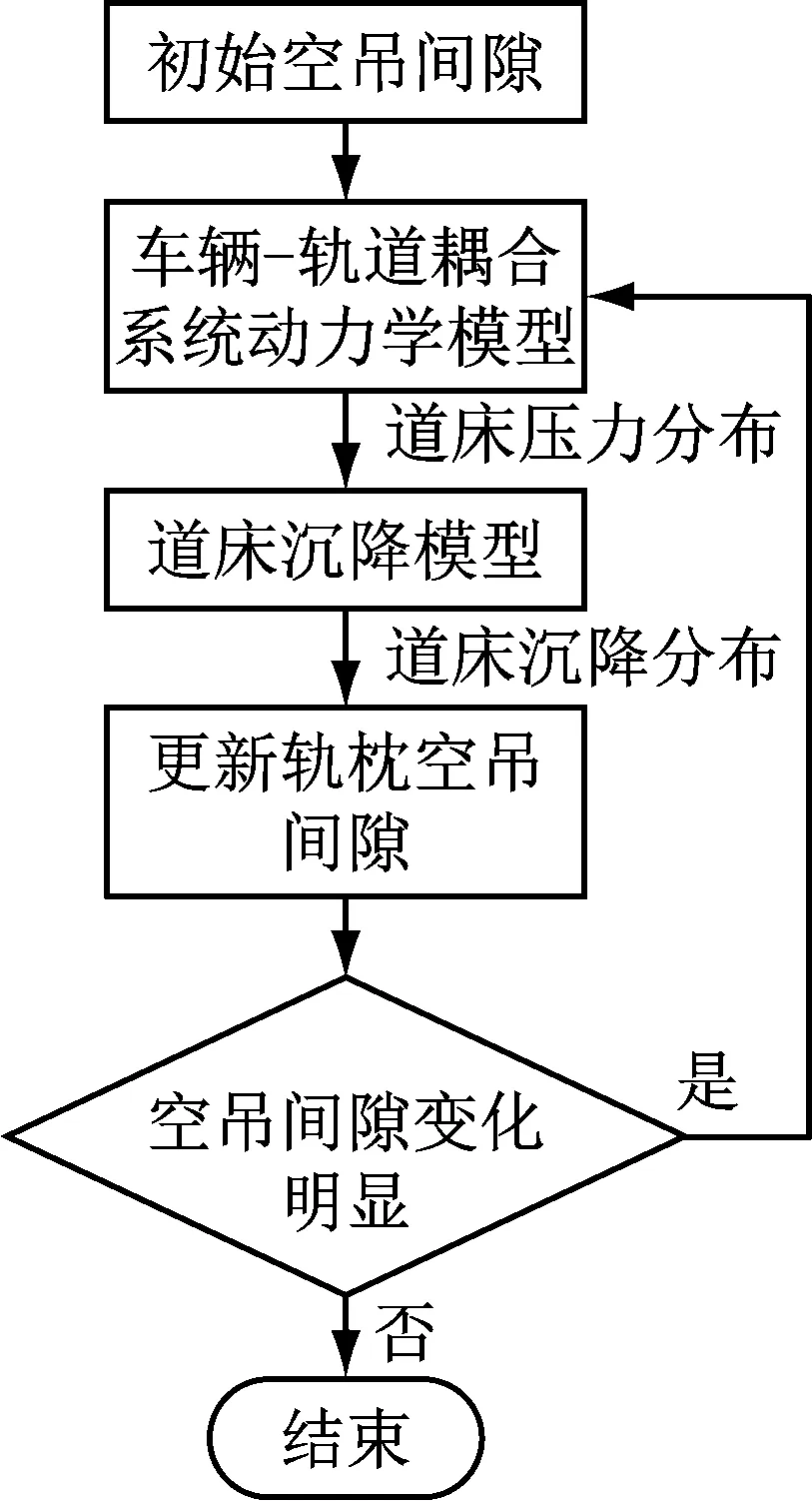
图7 迭代计算流程
2 轨枕单侧空吊
如图8b所示,车辆经过时轨枕承受的垂向载荷(66.9 kN)主要由两侧承担,中间区域受力较小.由于受到初始间隙的影响,轨枕空吊区域(1号区域)基本上不再承受车辆载荷,而与之相邻的2号区域承受的作用力显著增加,达到13 kN.此外,由于轨枕左侧受到局部空吊的影响,导致轨枕左侧非空吊区域承受的车辆载荷明显高于轨枕右侧的相应区域,如轨枕左侧2号和3号区域承受的作用力分别为13 kN和10 kN,而轨枕右侧相应的9号和8号区域承受的作用力仅为8 kN和7 kN.
随着车辆通过次数的增加、运量的增大(累积通过量5 000 t),轨枕下方道床在如图8b所示的载荷分布情况下产生不同程度的累积沉降,进而导致轨枕各区域出现不同程度的空吊间隙.如图9a所示,轨枕1号区域在初始3 mm空吊间隙的影响下不再承受车辆载荷,因而该区域的空吊间隙不再发生明显的变化,与之相邻的2号、3号区域由于受到的车辆载荷最大,导致该区域空吊间隙发展迅速,分别达到2.9 mm和1.9 mm.由于此时轨枕两侧依然为主要的承载区域,因而轨枕两侧的空吊程度明显高于轨枕中间区域.与此同时,随着轨枕各区域空吊程度的变化,轨枕下方道床所承受的车辆载荷也发生了相应的改变,由之前的两端承载转变为中间承载,即轨枕中间区域下方的道床成为主要的承载区域(达到11.5 kN),而两端区域空吊间隙较大,基本失去支承作用(见图9b).
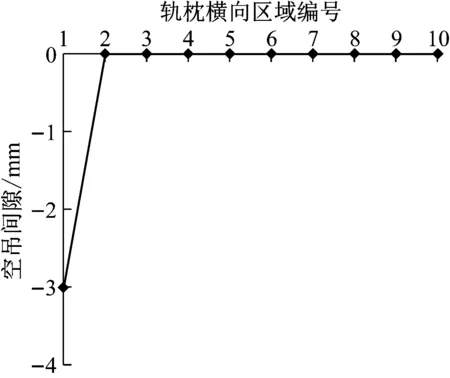
a 轨枕空吊间隙
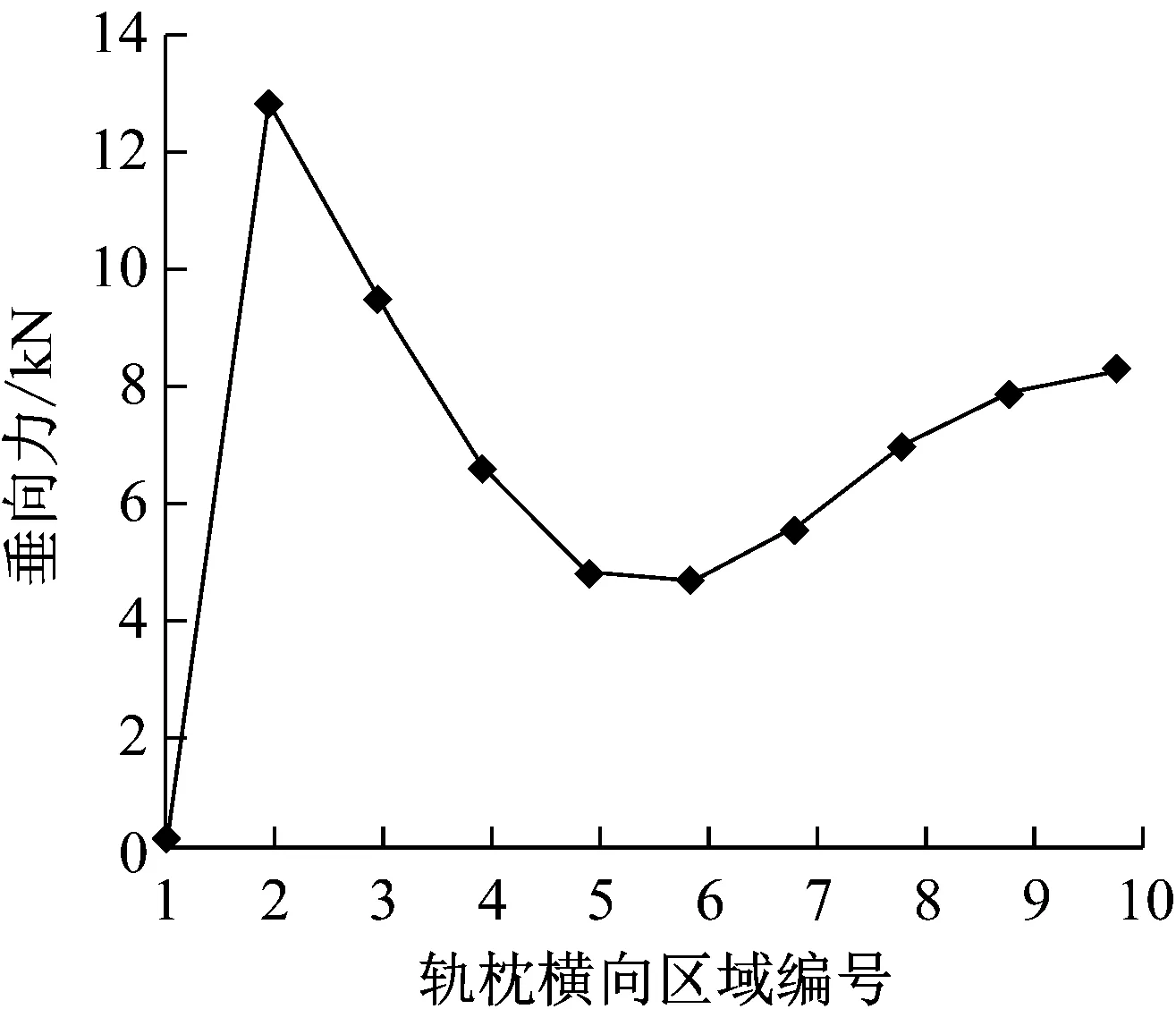
b 轨枕-道床作用力
Fig.8 Initial contact situation of sleeper and subgrade in condition of side voided sleeper
随着车辆通过次数的进一步增加(累积通过量达到15 000~600 000 t),从图10可以看出,轨枕各区域空吊间隙的发展速度明显变缓,最终大部分区域处于1.5 mm左右的空吊间隙.主要原因在于:一方面道床在车辆载荷的作用下逐渐被压实,导致沉降速度降低;另一方面,随着轨枕空吊程度的增加,轨枕的承载能力逐渐丧失,如当累积通过量达到600 000 t时,该轨枕仅承受31.61 kN的车辆载荷(相比于初始时刻减少了52.8%),而大部分的车辆载荷主要由相邻未出现空吊的轨枕承担.
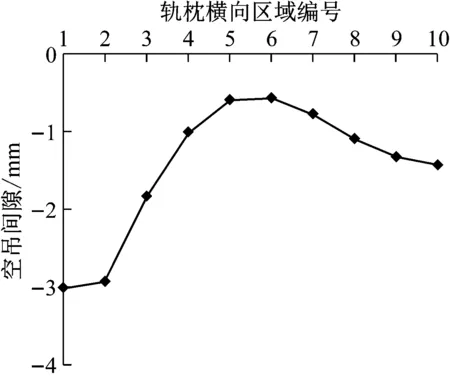
a 轨枕空吊间隙
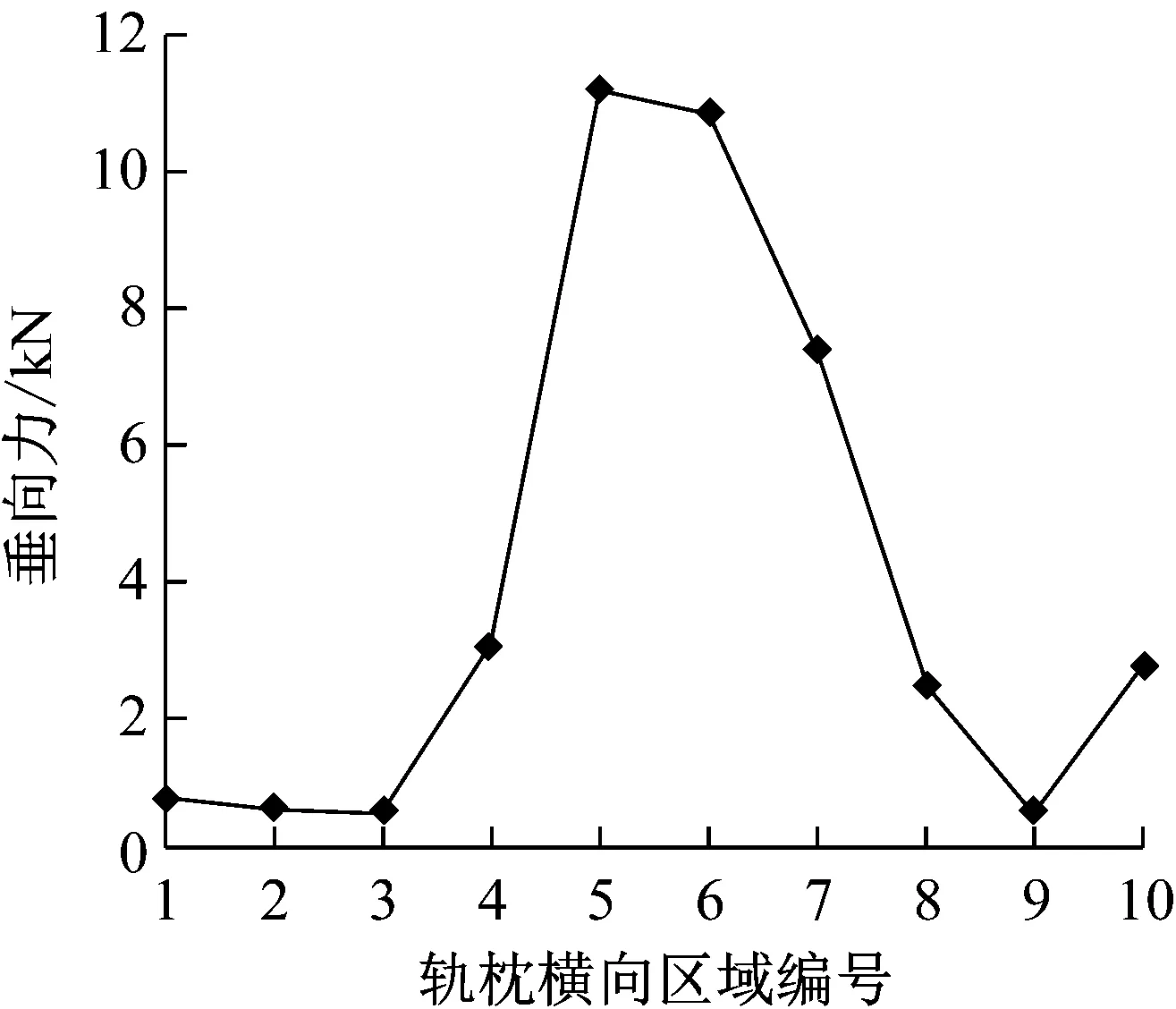
b 轨枕-道床作用力
Fig.9 Sleeper-subgrade contact situation in condition of side voided sleeper(5 000 t accumulative volume)
综上所述,当轨枕单侧出现局部空吊时,整根轨枕空吊状态的演变过程主要包括以下两个阶段:
(1) 初始阶段.轨枕两侧为主要承载区域,空吊程度发展较快;轨枕中部承载较少,空吊程度发展缓慢.此外,局部初始空吊间隙将加大临近区域的空吊发展速度.
(2) 稳态阶段.轨枕两侧区域在快速空吊后进入稳态发展阶段,此时轨枕中部为主要承载区域,空吊程度逐步加大,而轨枕两侧承载较少,空吊变化不明显.此外,由于该阶段整根轨枕出现大面积的空吊间隙,轨枕的承载能力大幅降低,空吊程度较初始阶段变化缓慢.
3 轨枕中部空吊
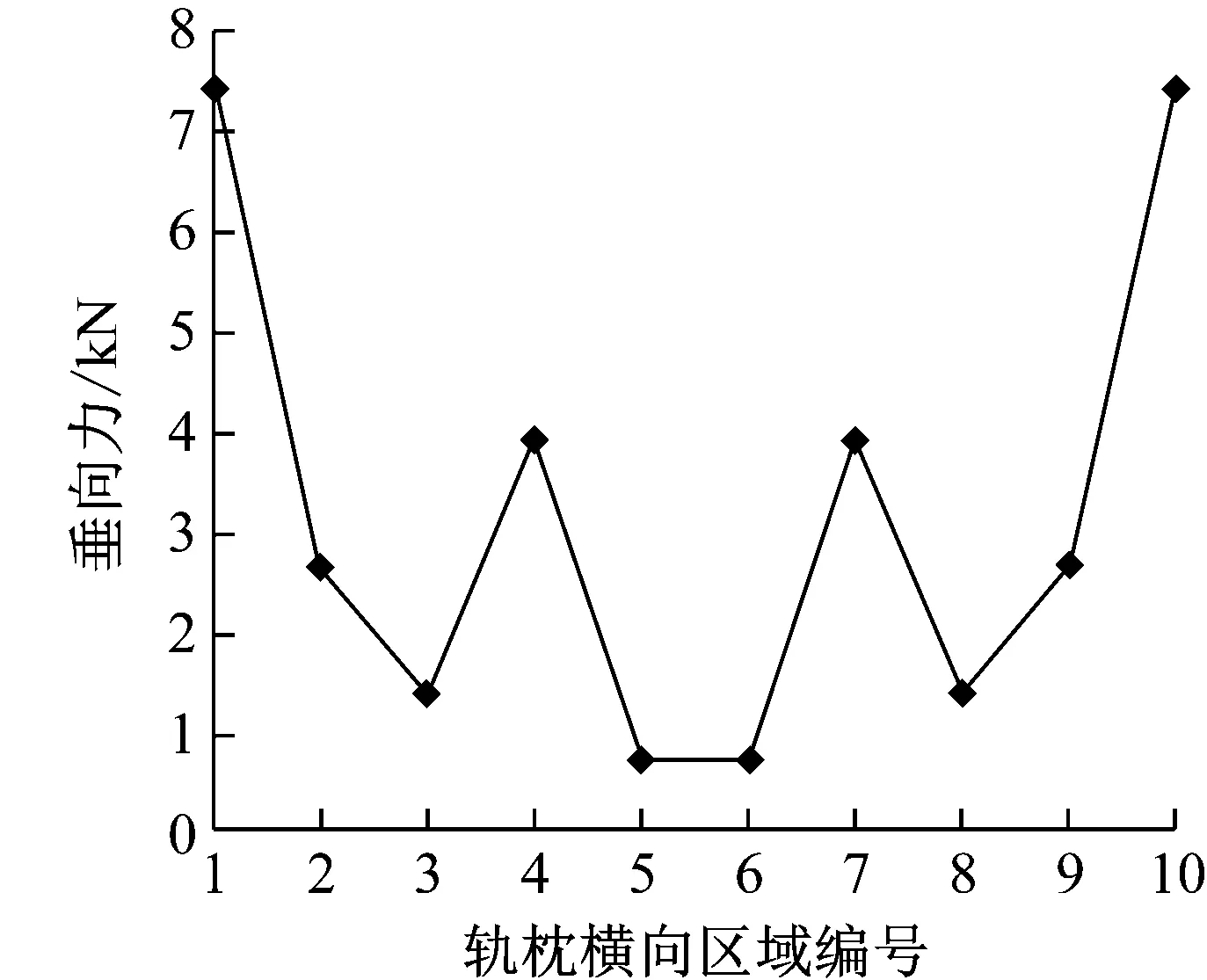
在轨枕中部出现空吊情况(如图11a所示,轨枕5、6号区域出现3 mm空吊间隙)下,车辆经过时轨枕承受的垂向载荷(67.7 kN)主要由位于钢轨下方的轨枕两侧承担,而轨枕中部空吊区域基本上不承受车辆载荷.此外,临近空吊区域的3号和8号区域承受的车辆载荷最大,达到8.8 kN(见图11b).

a 轨枕空吊间隙

b 轨枕-道床作用力
Fig.10 Sleeper-subgrade contact situation in condition of side voided sleeper(15 000~600 000 t accumulative volume)
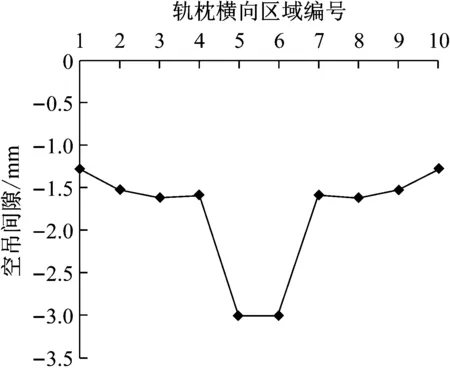
随着车辆通过次数的增加、运量的增大,轨枕下方道床在如图11b所示的载荷分布情况下产生不同程度的累积沉降,进而导致轨枕各区域出现不同程度的空吊间隙.如图12a所示,轨枕5、6号区域在初始3 mm空吊间隙的影响下不再承受车辆载荷,因而该区域的空吊程度不再发生明显的变化,而轨枕两侧由于受到较大的车辆载荷,导致该区域由于道床沉降而引发的空吊发展较快,达到1.5 mm左右.与此同时,随着轨枕各区域空吊程度的变化,轨枕下方道床所承受的车辆载荷也发生了相应的改变,轨枕承受的最大载荷区域由之前临近中部空吊的3号和8号区域转变为轨枕两端的1号和10号区域(见图12b).
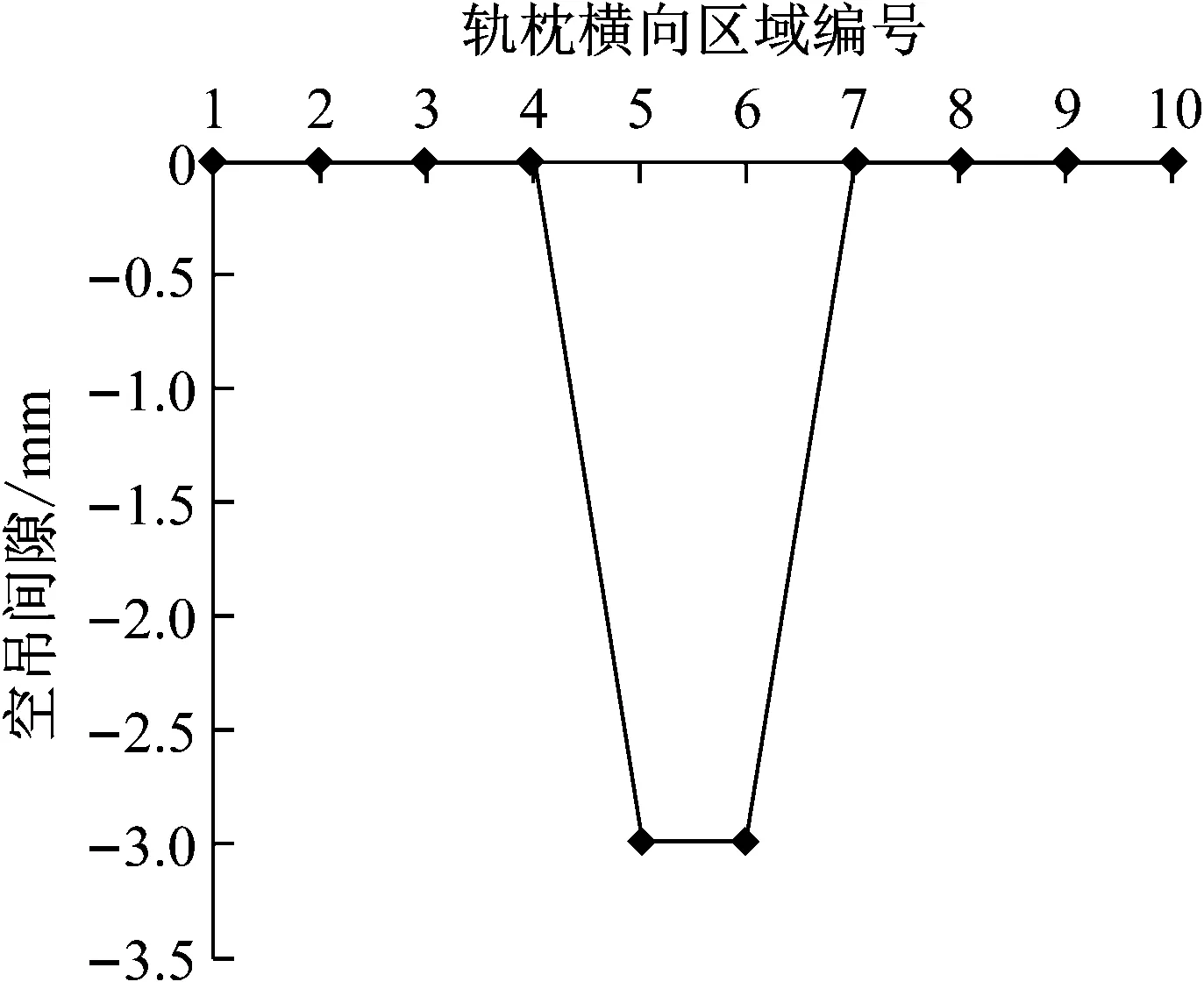
a 轨枕空吊间隙

b 轨枕-道床作用力
Fig.11 Initial contact situation of sleeper and subgrade in condition of central voided sleeper
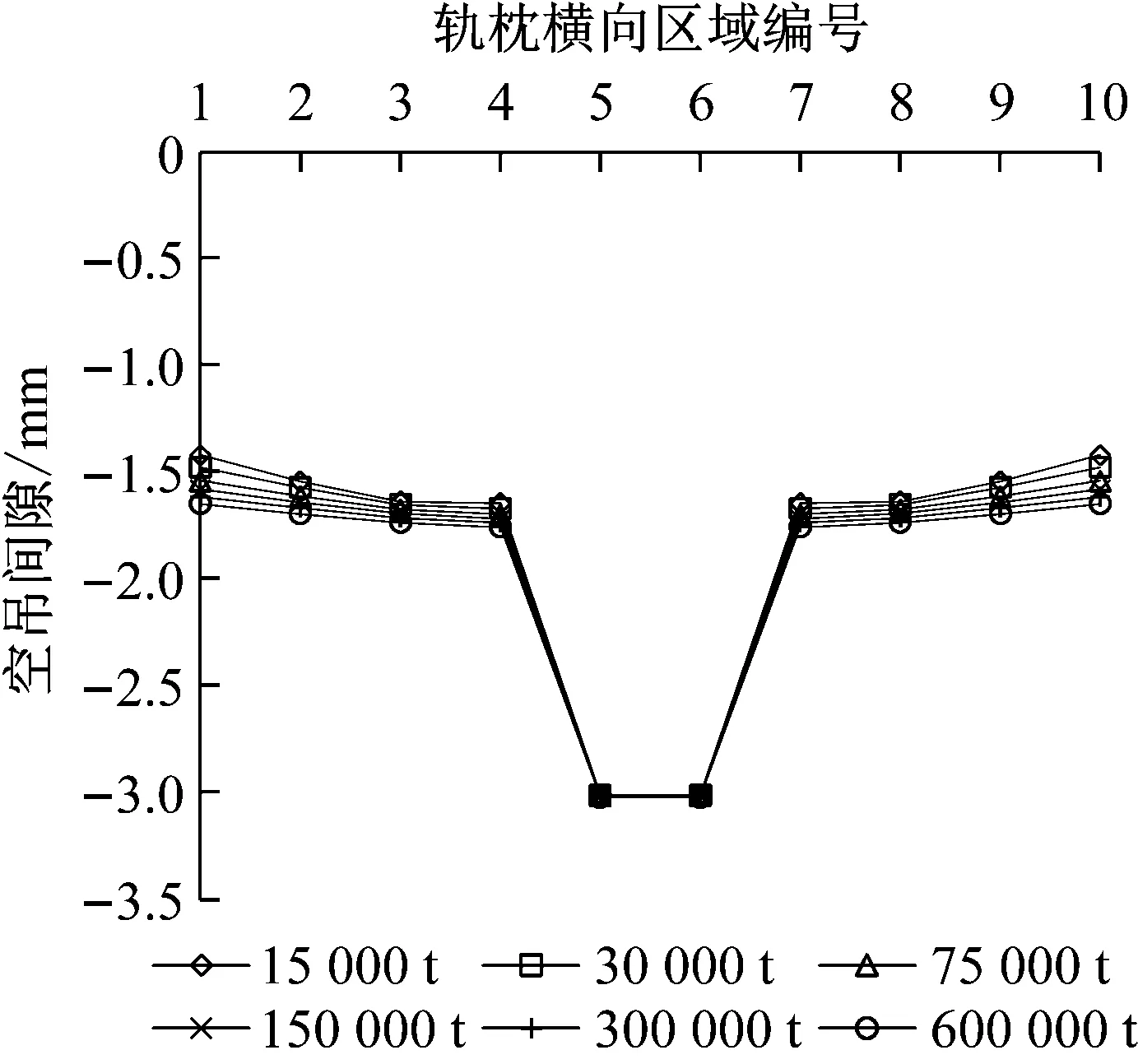
随着车辆通过次数的进一步增加,从图13可以看出,轨枕各区域空吊间隙的发展速度明显变缓,最终大部分区域处于1.7 mm的空吊间隙.主要原因在于:一方面道床在车辆载荷的作用下逐渐被压实,导致沉降速度降低;另一方面,随着轨枕空吊程度的增加,轨枕的承载能力逐渐降低,如当累积通过量达到600 000 t时,该轨枕仅承受26.8 kN的车辆载荷(相比于初始时刻减少了60.4%),而大部分的车辆载荷主要由相邻未出现空吊的轨枕承担.
综上所述,相比于轨枕单侧空吊,当轨枕中部出现空吊时,整根轨枕空吊状态的演变过程相对简单,轨枕两端始终为主要的承载区域,并在通过车辆载荷的作用下空吊间隙显著增加并逐渐趋于稳定,而出现空吊的轨枕中部区域由于不再承受车辆载荷,空吊间隙未发生明显变化.
4 结论
(1) 在车辆-轨道耦合系统动力学模型和道床沉降模型的基础上,提出了一种基于迭代计算的轨枕空吊预测方法,为进一步研究轨枕局部空吊后的动态演变过程提供了有效途径.此外,本文模型可以更好地研究车辆-轨道系统在耦合振动状态下的演化过程,在轨枕疲劳裂纹、道床不均匀沉降等长时效动力预测、演化机制方面均可做深入的拓展研究.
a 轨枕空吊间隙
b 轨枕-道床作用力
Fig.12 Sleeper-subgrade contact situation in condition of central voided sleeper(5 000 t accumulative volume)
(2) 当轨枕单侧出现空吊时,空吊区域的承载力明显降低,而与之相邻区域承受的车辆载荷增加,导致相邻区域轨枕空吊间隙发展较快,从而形成轨枕空吊区域由两端向中间扩展的动态演变过程.此外,随着轨枕空吊区域的不断扩大,整根轨枕的承载力大幅降低,大部分的车辆载荷主要由相邻未出现空吊的轨枕承担,因而该轨枕的空吊发展程度逐渐趋于平缓,最终大部分区域存在1.5 mm左右的空吊间隙.
(3) 当轨枕中部出现空吊时,整根轨枕空吊状态的演变过程相对简单,轨枕两端始终为主要的承载区域,并在通过车辆载荷的作用下空吊间隙显著增加并逐渐趋于稳定,出现空吊的轨枕中部区域由于不再承受车辆载荷,空吊间隙未发生明显变化.
a 轨枕空吊间隙
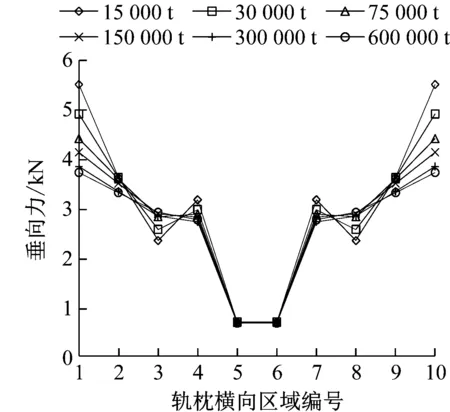
b 轨枕-道床作用力
Fig.13 Sleeper-subgrade contact situation in condition of central voided sleeper(15 000~600 000 t accumulative volume)
