600kN超大推力电磁振动试验台动圈结构的模态分析与优化

仝宁可，杜环宇，李鸿光，刘 营，孟 光

（1.苏州东菱振动试验仪器有限公司，江苏 苏州215010；2.上海交通大学 机械系统与振动国家重点实验室，上海200240）

振动试验台系统是一种能够产生一定频率范围内的振动并实现振动控制的试验仪器系统，其主要任务是通过一定的控制方式，将规定的运动和能量传递给待试验产品或者零件。伴随我国在航天领域的探月工程、载人航天等国家重点工程的持续进步，对振动试验设备的推力需求在不断加大，国内科研单位迫切需求更大推力的电磁振动试验设备。本研究拟开发的电磁振动试验台，其峰值推力可高达600 kN。动圈结构作为电磁振动台台体运动的核心部件，是试验台激振力的来源，担负着整个装置的“心脏”作用。同时，动圈结构的1 阶轴向共振频率还决定了振动台工作频率的上限范围[1]。

由于动圈结构的复杂性，在设计初期，其1阶轴向共振频率一般只能靠经验估算。近年来，随着有限元方法的迅速发展，学者们针对振动试验台系统利用有限元分析进行了广泛研究。李红强等[2]建立了一般动圈模型的简化快算模型，并通过有限元方法验证了快算模型的实用性。随后，范宣华、崔志嘉等人[3-5]建立了动圈结构的有限元模型，并将仿真结果与试验结果进行了对比验证。宦海洋等[6]基于VE-1031 型电动振动台的动圈结构进行建模，得到了模型的空台传递函数并且进行了模态研究。张逸波等[7]针对200 kN振动台的动圈结构进行了建模仿真，得到了系统的传递函数和响应曲线。陈小慧、夏天凉等[8-9]完成了对电动振动台的动力学建模并进行了设备扩展台面的设计。孟繁莹等[10]考虑了动圈模型中的磁-结构耦合效应，分析了电磁力对动圈输出的影响。

然而在上述研究中，主要存在以下不足：其一，动圈结构作为高度对称结构，对称模态和局部模态广泛存在，很难从模态分析结果中直接提取1 阶轴向共振模态；其二，绝大多数研究只进行了动圈模型的有限元分析和验证，而未针对提高动圈工作频率进行优化。另外，在本研究中，为满足试验台设备大推力和高强度的要求，作为核心驱动部件的动圈约重达400 kg，在约束条件相同的情况下其共振频率会更低。因此，需要对动圈结构进行优化以提高其工作频率上限。

1 振动台动圈结构有限元模型的建立

1.1 动圈模型的结构特征

忽略螺孔和凹槽等细小特征，600 kN 超大推力电磁振动试验台的动圈模型及坐标轴选取如图1所示。

图1 电磁振动试验台动圈结构模型

模型主要由动圈台面、动圈侧板、竖直筋板、中心圆筒、绕组骨架和驱动线圈绕组等部分组成。

其中，动圈台面是动圈最上端的特征结构，动圈台面上有环形立板和辐射立板，环形立板从内而外分三层，辐射立板每两片间隔45 度、共8 片；竖直筋板是连接动圈上部和下部的特征结构，也是动圈台面推动台面工作时的主要承力结构，与辐射立板相对应、共8 片；动圈侧板分布在相邻的竖直筋板之间，能够改善动圈台面的受力状况并一定程度上提高振动的稳定性；中心圆筒上开有静压轴承安装孔，上端孔主要用于连接台面悬挂，下端孔用于连接支撑装置；驱动线圈绕组是由铝制线圈紧密绕制而成，表面涂有环氧树脂绝缘层。

该模型所使用的材料参数及上述结构的尺寸参数如表1所示。

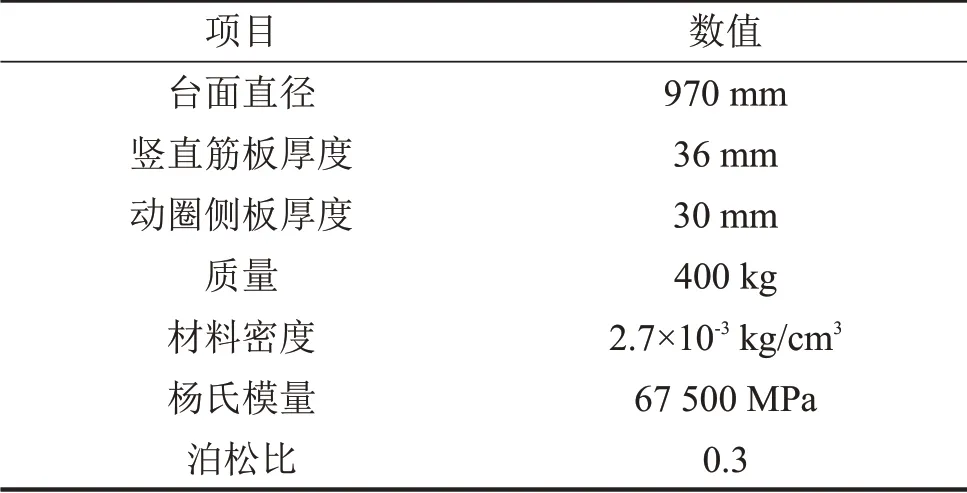
表1 电磁振动试验台动圈结构主要参数表

1.2 动圈模型模态分析的约束定义

动圈结构在电磁振动试验台实际工况下所处的约束环境如图2所示。

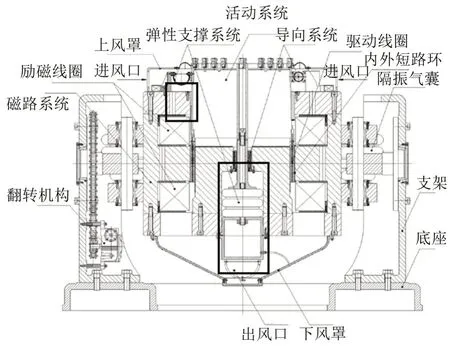
图2 电磁振动试验台动圈实际工况下的约束环境

可将其简化为如下3种约束形式：其一，动圈侧板受到U 型悬挂弹簧的导向约束，动圈侧板和U 型悬挂弹簧之间通过螺栓连接紧固，在ANSYS模型动圈侧板选取弹簧紧固点，约束节点X方向和Z方向的自由度，仅保留Y方向（动圈轴向）的自由度；其二，中心圆筒底部插入导向棒的导向约束，将模型中所有与导向棒接触的圆筒内表面节点同样约束X方向与Z方向的自由度；其三，动圈结构底部空气弹簧提供的支承刚度，为了将空气弹簧提供的轴向刚度均匀分布在动圈结构底部，将空气弹簧刚度等效为均匀连接在中心圆筒底部的并联弹簧组。

在ANSYS14.5中，弹簧单元选用COMBIN14单元，其余实体结构选用SOLID45单元。空气弹簧刚度由式(1)根据振动台系统最低阶共振频率求得

根据动圈模型，上述等效并联弹簧组共包含80根COMBIN14 弹簧。试验测得系统最低阶共振频率为5 Hz，经过计算，每根弹簧的刚度约为4.9 N/mm。

图3 ANSYS约束定义后的电磁振动试验台动圈模型

2 动圈结构的模态分析及缩减模型

2.1 完整动圈模型的模态分析

本研究选用Block Lanczos 方法作为模态求解方法，求解器设置振型提取阶数为50 阶、频率求解范围为1 Hz～3 000 Hz。ANSYS求解器运行时间大约持续1 小时左右，求解结果的部分关键阶模态数据如表2所示，其中，1阶轴向振型如图4所示。

图4 电磁振动试验台动圈的1阶轴向振型(1 361.4 Hz)

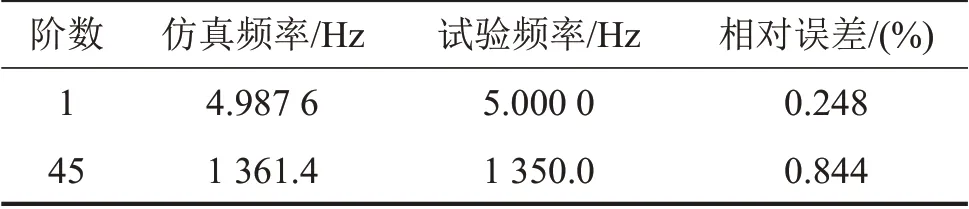
表2 动圈结构的ANSYS模态分析结果及误差

2.2 动圈模型1阶轴向振型的识别

由于动圈结构的复杂性和高度对称性，模态分析不仅会出现许多局部模态，还会包含许多对称模态，1阶轴向振型容易淹没在众多模态结果中。在以往研究中，一般采用在试验测得的频率结果周围进行人工搜索的方式寻找轴向振型，这将削弱有限元分析对实际设计过程的指导意义。为了从动圈结构各阶振型结果中准确提取1 阶轴向振型，本文定义了一个新的振型特征—有效质量权重(Efficient Mass Percentage，EMP)。

在某阶振型下，有限元模型沿某一方向的有效质量(Efficient Mass，EM)可由式(2)求得

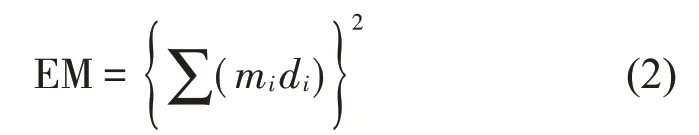
有效质量(EM)指标能够反映模型沿该方向参与该振型的程度。模型沿X、Y、Z坐标轴的有效质量，可以从ANSYS 模态分析的各阶模态结果中导出。模型的1阶轴向振型区别于其他振型最显著的特点即在该阶振型下，模型整体沿动圈轴向（Y方向）的振动相比其他方向显著得多。所以，本文提出有效质量权重(EMP)概念，尤其关注沿轴向（Y方向）的有效质量权重。某阶振型下模型沿Y方向的EMP定义式如式(3)

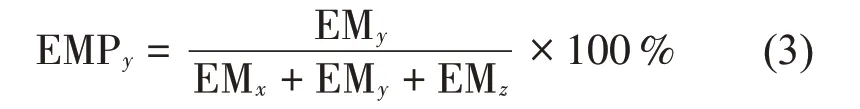
根据定义式，EMPy的数值越大，表明该阶振型下动圈模型各质量单元的轴向位移相对其余方向更加显著。换句话说，EMPy数值越大的振型越有可能是动圈模型的轴向振型。

根据EMP 识别技术发现，在ANSYS 模态分析求解的50 阶振型中，除去第1 阶刚体振型，EMPy数值大于1%的模态振型只有4阶。这说明EMP方法在识别轴向振型上具有良好的识别度。这4阶振型的EMPy数值如表3所示。

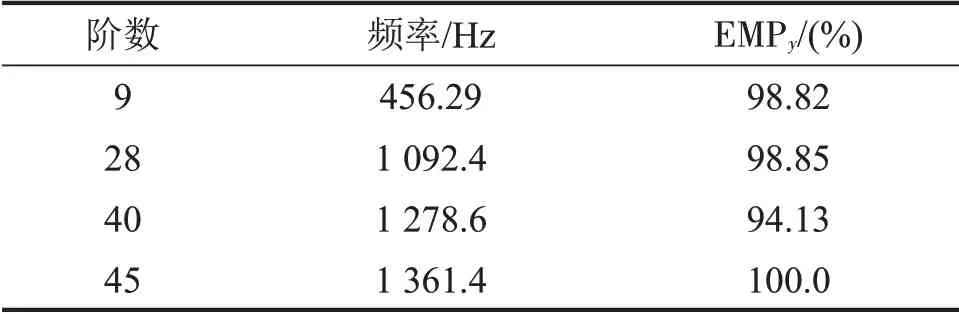
表3 部分阶振型(EMPy ＞1%)的Y方向有效质量权重

由上文可知，第45 阶振型即为动圈模型的1 阶轴向振型。从表3中可以得到相同结果，因为该阶振型的EMPy数值高达100.0%。另外，需要说明的是，其余3 阶振型虽然EMPy数值也很高，不过主要表现为驱动线圈绕组或者竖直筋板的局部模态，模态振型如图5所示。

图5 电磁振动试验台动圈模型的第9阶、第28阶与第40阶模态振型

2.3 动圈缩减模型的模态分析

对于动圈结构这样的复杂模型，基于有效质量权重(EMP)的轴向振型识别能够较好地识别模型的轴向振型，消除绝大多数模态的干扰，却无法排除模型出现的局部轴向模态。为解决该问题，针对动圈结构的高度对称性，采用了动圈的1/16 缩减模型。该缩减模型由动圈模型切割而成，两切割面均沿半径方向通过动圈模型中心轴。切割面之间夹角为22.5度。缩减模型很好地保留了动圈模型的结构特征，同时极大简化了模型复杂程度、削弱了分析中局部模态和对称模态出现的频率。

对缩减模型的约束处理情况与前文基本一致。值得注意的是，缩减模型还需模拟完整动圈对称结构对缩减模型的约束效果。该约束通过在COMSOL5.2软件中定义被切割面的对称约束实现。

通过缩减模型进行模态分析的求解，结果表明，在刚体振型之后，随即出现了动圈模型的1 阶轴向振型，原完整模型所产生的对称模态以及局部模态均被消除。模型的1阶轴向振型如图6所示，共振频率为1 358.2 Hz，与完整模型频率误差为0.235%，与试验频率误差为0.607%。

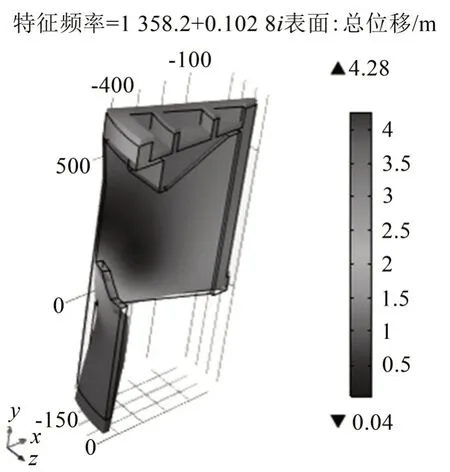
图6 动圈缩减模型的1阶轴向振型(1 358.2 Hz)

3 振动台动圈结构的优化设计

3.1 动圈模型的灵敏度分析

在对模型进行优化设计之前，需对各主要模型参数进行灵敏度分析。灵敏度分析能够确定相关模型参数对动圈1 阶轴向共振频率的影响趋势，进而初步确立某些指标为待优化参数、同时还能了解这些参数的初始优化方向。

本研究中，首要优化目标为提高动圈结构的1阶轴向共振频率，限制条件是动圈结构的质量不能大幅增加，控制在450 kg 以内。本文分别选取以下尺寸参数为灵敏度分析对象：竖直筋板厚度(L1)、侧板厚度(L2)、台面直径(D)以及圆角半径(r)。各尺寸参数分别对动圈1 阶轴向共振频率、动圈质量的灵敏度分析结果如表4所示。

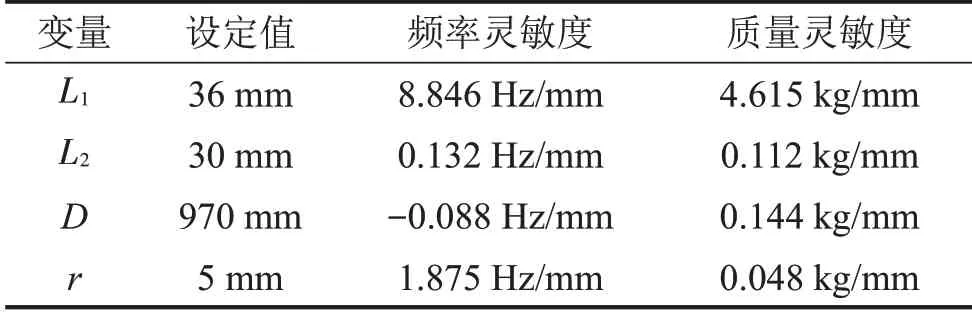
表4 动圈1阶轴向频率、质量关于主要尺寸参数灵敏度

根据灵敏度分析结果，侧板厚度(L2)和台面直径(D)参数对动圈模型的1 阶轴向共振频率影响程度较小，不宜作为优化指标；直接改变动圈模型的竖直筋板厚度(L1)能显著地改变动圈的1 阶轴向共振频率，但同时会显著地增加质量，需考虑其他优化方案；圆角半径(r)，改变这一参数不仅能较显著地提高动圈模型的1 阶轴向共振频率，且不会明显增加模型质量，应作为优化参数。

3.2 动圈竖直筋板的斜度优化

如上文所述，直接增大动圈筋板厚度会造成大幅增加动圈结构质量的不利影响，本文提出了对竖直筋板沿径向增加斜度的解决办法，使其沿半径方向由内侧向外侧逐渐增加厚度，从而尽量减小对模型质量的影响。在COMSOL建模中，该解决方法通过对动圈缩减模型进行拔模处理来实现，衍生出拔模角度(θ)和拔模中面位置比例(σ)2个定义参数，如图7所示。

图7 定义参数：拔模角度(θ)和拔模中面位置(d)标识

拔模中面位置比例(σ)是用来表明斜度产生过程中厚度不变位置的参数，由拔模中面位置(d)和筋板总长(L)计算所得，计算方法如式(4)

3.3 动圈模型的优化结果

根据灵敏度分析结果，最终选定动圈模型的圆角半径(r)、拔模角度(θ)和拔模中面位置比例(σ)作为动圈模型的优化参数。

优化过程中，设定圆角半径(r)的变化范围为0～30 mm；在工程中，较大的筋板斜度会使筋板内侧根部变得薄弱，所以设定拔模角度的变化范围为0°～3°、拔模中面位置比例的变化范围为0.2～0.8。采用动圈缩减模型作为初始模型，优化目标为模型1阶轴向共振频率（第2 阶模态频率）最大，约束条件为动圈缩减模型质量m＜28.125 kg。

通过COMSOL5.2 软件进行优化分析，各优化参数的最终优化结果如表5所示。优化后的1 阶轴向共振频率为1 546.9 Hz。

表5 动圈模型优化参数的优化结果

4 结语

本文建立了600 kN 超大推力电磁振动试验台动圈结构的有限元分析模型，根据施加实际工况约束条件，通过模态分析得到了模型的各阶模态。为从众多模态振型中识别1 阶轴向振型，定义了有效质量权重(EMP)概念，利用其成功进行模型的轴向振型识别并通过验证。为消除模态分析中产生的对称模态和局部模态，结合动圈结构的高度对称性特点，建立了动圈的1/16缩减模型，极大简化了动圈结构，模态分析取得良好结果。最后，针对提高动圈结构的1 阶轴向共振频率要求，先后进行了各主要尺寸参数的灵敏度分析和优化设计。根据灵敏度分析定量分析了各参数对动圈1 阶轴向共振频率、质量的影响程度，确定了优化参数指标，提出了一种可行的动圈结构优化方案。