一种基于流形学习和KNN算法的柴油机工况识别方法
2019-06-25江志农赵南洋赵飞松高佳丽张进杰
江志农,赵南洋,夏 敏,赵飞松,高佳丽,张进杰
(1.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京100029;2.中石化重庆天然气管道有限责任公司,重庆408000;3.北京化工大学 压缩机技术国家重点实验室压缩机健康智能监控中心,北京100029)
柴油机作为一种典型的内燃机械,在石油钻井、舰船动力、应急发电、工程机械等等工业领域应用十分广泛。但由于柴油机机械结构复杂、易损件多、工作条件恶劣,实际运行中故障频发,如失火、气门磨损、拉缸、连杆断裂等,易造成严重的经济损失并影响安全稳定生产。因此,柴油机故障监测诊断技术一直以来都是研究热点。在离线测试方面,可通过定期采集油品,进行光谱、铁谱分析,对润滑油内的各类元素含量进行测试[1-2]。应用振动分析方法、噪声分析方法进行柴油机故障诊断已有一定的研究,梅检民等提出了一种基于高阶累积量的振动信号分析方法,采用高阶累积量的AR双谱,对连杆轴承故障加速振动信号进行分析[3],沈虹等提出了一种基于角域四阶累积量切片谱的柴油机连杆轴承故障特征提取方法[4],程利军等提出了一种基于阶比跟踪及共振解调的连杆轴承故障诊断方法[5]。
但是,由于柴油机工况复杂,如功率、转速及其他工作环境的变化,导致机组监测信号多变,给故障监测诊断带来了较大的难度。例如,柴油机故障监测系统的报警线设置,若按照单一报警线设置,在变负荷工况下将会产生较多的误报、漏报;若根据机组运行状态设置,则需要对柴油机运行状态数据开展深入的分析研究,以机组运行状态的自动识别为基础。
因此,本文提出了一种基于流形学习和KNN算法的柴油机工况识别方法,可实现对柴油机运行状态的自动分类。方法融合了机组的振动、温度、压力等多源信号特征构建特征向量;通过流形学习t-分布邻域嵌入算法(t-SNE)实现特征向量的维数约简和敏感特征提取,降低数据分析处理难度;最后通过K 最近邻分类算法(KNN)构建了自动分类模型,完成柴油机运行负荷状态的自动分类。
1 流形学习与KNN算法
1.1 流形学习方法
流形学习(Maniflod Learning)是一种非线性降维方法[6],首次由Bregler和Omohundro提出,假设数据是均匀采样于一个高维欧氏空间,其采样点的分布具有低维流形的结构特征,流形学习就是从高维的采样数据中提取出低维流形结构,并求出相应的嵌入映射,从而实现数据特征维数的约简及数据可视化[7]。
目前,其算法包括t-分布邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)[8]、等距映射(Isometric Feature Mapping,Isomap)[9-10]、局部线性嵌入(Local Linear Embedding,LLE)[11]、随机邻域嵌入(Stochastic Neighbor Embedding,SNE)[12]等。其中t-SNE 算法是一种利用概率形式的降维算法,来缓解在低维空间中映射数据点之间拥挤问题。t-SNE 算法用KL散度(Kullback-Leibler divergence)来度量两个分布之间的相似性,使数据在低维空间上有聚类的效果,且不同类别的数据簇之间存在一定的距离,这对使用分类算法来实现柴油机运行工况识别提供了良好条件,因此本文选用t-SNE 算法来对柴油机运行工况特征向量进行降维及可视化处理。
t-SNE算法的步骤如下:
(1)原始数据,记为:X={x1,x2,···,xn};
(2)设置迭代次数T,学习速率η,动量α(t);
(3)计算成本函数参数(perplexity Perp)
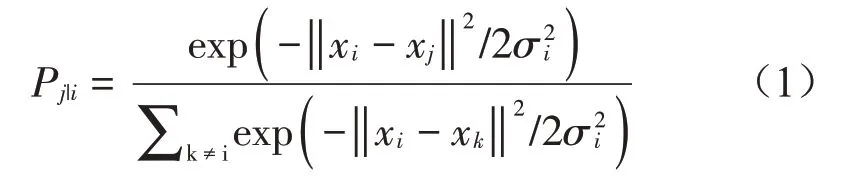
上式中σi是数据点xi的高斯方差;
(5)计算低维相似度qij
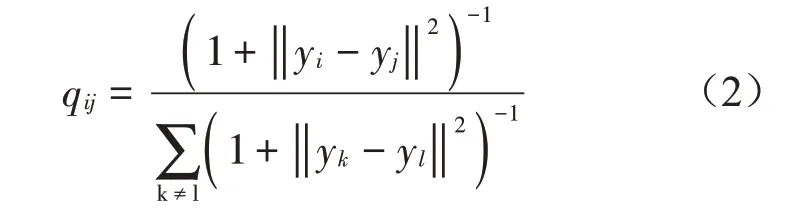
(6)计算KL散度(Kullback-Leibler divergence)

上式中KL散度是Q和P之间的相似度的度量;
(7)计算梯度最小化KL散度
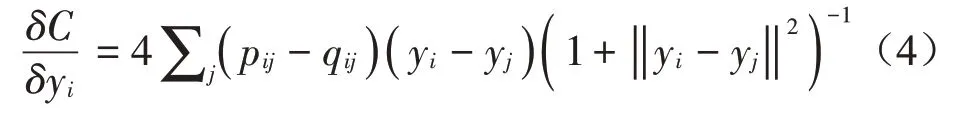
(8)更新
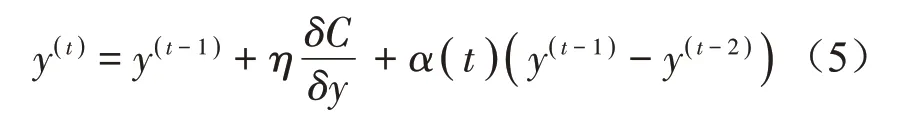
(9)循环迭代步骤(5)-步骤(8),迭代T次;
(10)最终得到低维数据
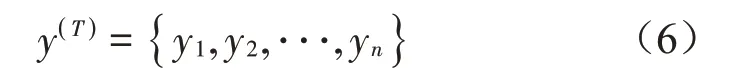
1.2 KNN算法
K最近邻分类算法(KNN)被广泛应用于数据挖掘和数据分类。如果待分类样本的样本数据点在空间中有K个距离最近样本数据点,其中某一类别的数据点占绝大多数,则KNN算法判定该样本数据点属于这个类别。
KNN 算法在待识别数据点与样本数据点之间的距离度量主要有欧式距离,曼哈顿距离和闵科夫斯基距离,其中闵科夫斯基距离定义如下

其中:d为维数,p为范数。当p=1时为曼哈顿距离;当p=2时为欧式距离。
本文选用欧氏距离作为KNN 算法待识别数据点与样本数据点之间的空间距离的度量。欧式距离定义如下

2 柴机油运行负荷状态识别方法
2.1 方法处理流程
本方法的处理流程图如图1所示。
首先根据柴油机监测信号进行多信号工况敏感特征参数提取,形成数据样本、测试样本和待识别工况数据,一起进行流行学习t-SNE算法降维。设定K值区间,使用降维后的样本数据和测试数据对KNN工况识别模型进行K值优化,确定识别率最高的K值的KNN模型进行工况识别结果输出。
2.2 柴油机实验台应用
(1)实验台机组介绍
实验台柴油机为TBD234V12柴油机,机组如图2所示,其主要技术参数如表1所示。
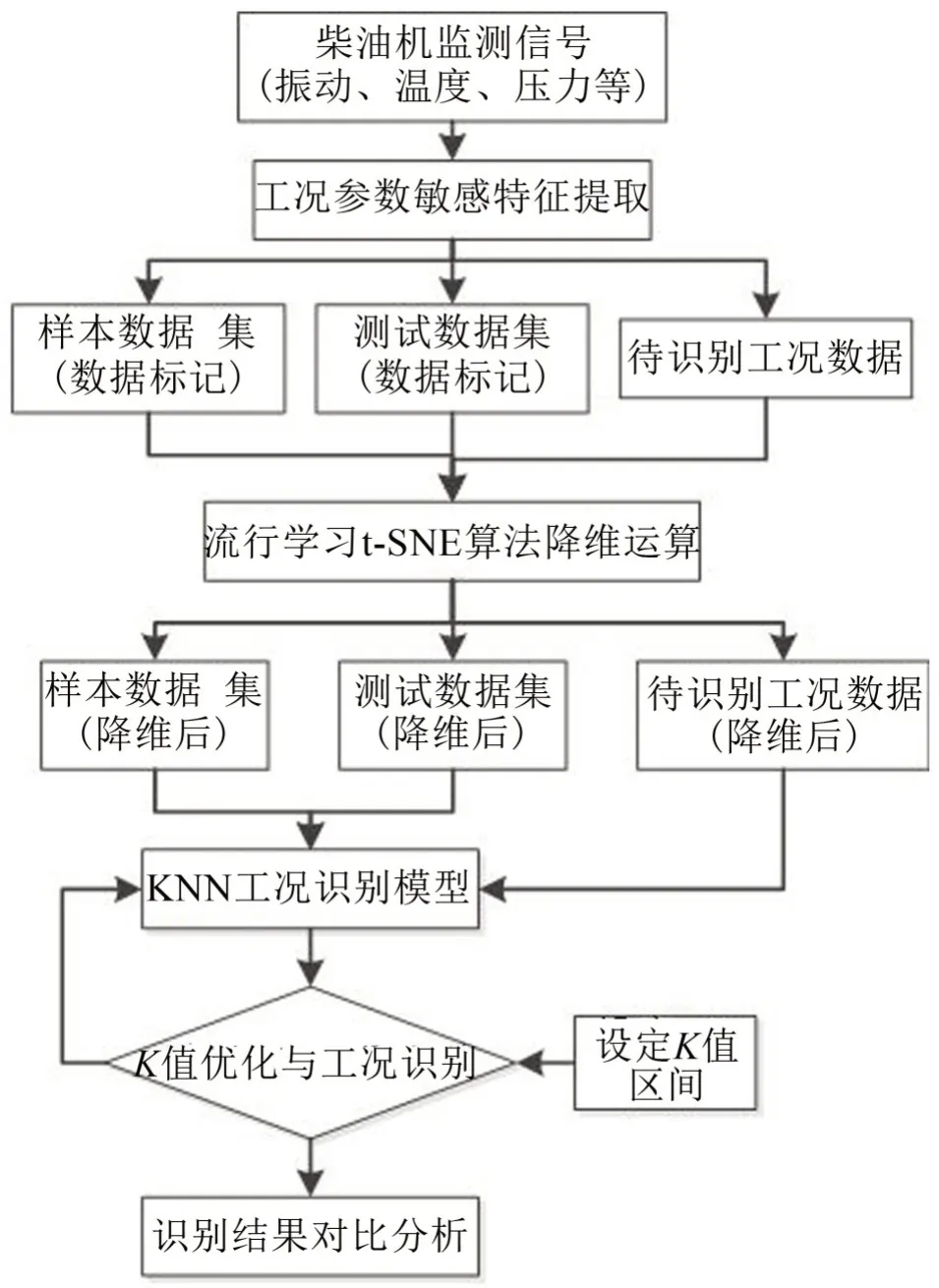
图1 方法处理流程图

表1 TBD234V12缸柴油机主要技术参数

图2 实验台TBD234V12型柴油机
该机组已自带部分温度、压力传感器,可实现对总排气温度、冷却水温度、润滑油压力等参数的在线监测。同时,在该机组上新增了振动、瞬时转速、活塞上止点信号传感器,对缸盖振动、曲轴箱振动、齿轮箱振动、涡轮增压器振动、瞬时转速、活塞上止点信号进行在线监测。从上述测点信号中,构建了如表2所示的信号特征集。
(2)正常状态下工况分类
对机组正常状态下不同负荷、不同转速状态的数据进行测试应用,共计12种工况。
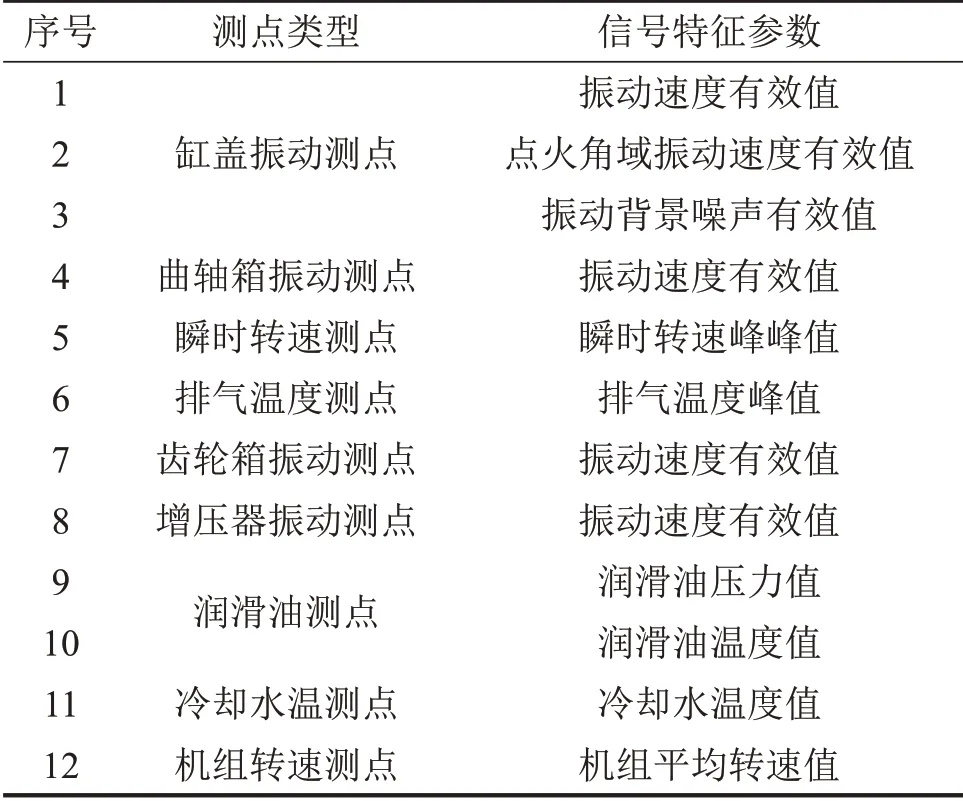
表2 多源信号监测参数特征集
Ø 转速1 500 r/min,扭矩700 Nm,1 000 Nm,1 300 Nm。
Ø 转速1 800 r/min,扭矩700 Nm,1 000 Nm,1 300 Nm,1 600 Nm。
Ø 转速2 100 r/min,扭矩700 Nm,1 000 Nm,1 300 Nm,1 600 Nm,2 200 Nm。
分类结果如下图4-图6所示。
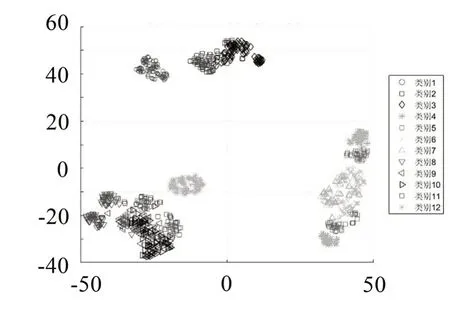
图4 t-SNE算法二维映射降维结果

图5 t-SNE算法三维映射降维结果

图6 KNN算法识别结果
图4和图5分别为二维和三维映射下的12种工况数据的分布情况,3种转速下的数据在空间3个地方集聚,同转速不同负荷的数据在集聚区团聚分布。图5为最优K值下的KNN算法二维和三维各工况识别率图,由图显示,三维下的KNN识别率优于二维。
(3)故障状态下工况分类
由于柴油机机械结构复杂,激励众多,常常发生故障。在柴油机发生故障的情况下,其运行工况的识别准确率必然受到影响。本文针对柴油机常见的气门间隙故障,使用耦合了故障的监测数据来研究故障对柴机油运行工况识别结果的影响。
实验工况共计6种:
Ø 转速1 500 r/min,扭矩700Nm,1 300 Nm;
Ø 转速1 800 r/min,扭矩700 Nm,1 300 Nm;
Ø 转速2 100 r/min,扭矩700 Nm,1 300 Nm。
分类结果如下图7-图8所示。
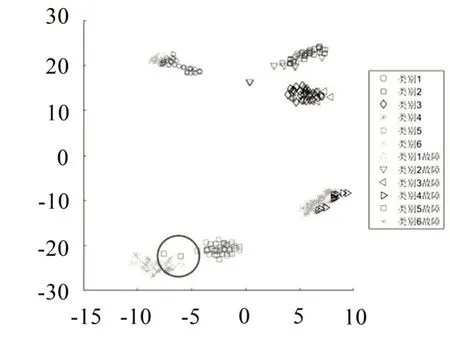
图7 t-SNE算法二维映射降维结果
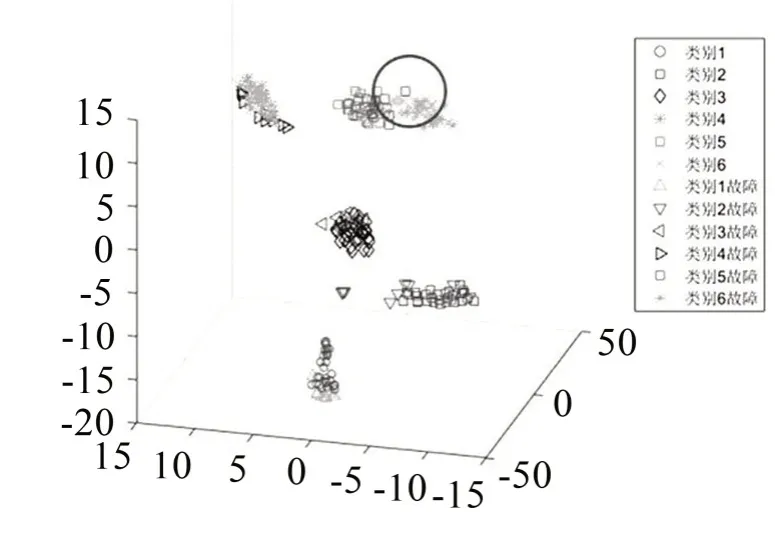
图8 t-SNE算法三维映射降维结果

表3 气门磨损状态下工况三维识别结果
图7和图8分别为二维和三维映射下的6 种工况故障耦合数据的分布情况,6种工况数据分别在空间集聚,部分故障数据点偏移数据集。由表3显示为气门磨损状态下工况三维识别正确率略有降低。
2.3 结果分析
实验台机组正常状态下的12种运行工况数据,分别使用t-SNE 算法向二维和三维空间映射,采用KNN算法识别,二维和三维空间的工况数据均得到了较好的分类,且三维空间上KNN综合识别率优于二维。
气门磨损故障数据集的工况识别结果显示,部分故障数据点偏移正常数据集,KNN识别率在工况转速1 500 r/min,扭矩1 300 Nm 和工况转速2 100 r/min,扭矩700 Nm降低,但整体识别准度仍较好。
3 方法的进一步验证与对比
3.1 工业柴油机测试结果与分析
以某20 缸大型柴油机监测数据为基础,利用5种负荷状态(0%,50%,85%,100%,110%)监测数据进行方法验证,结果如下所示。
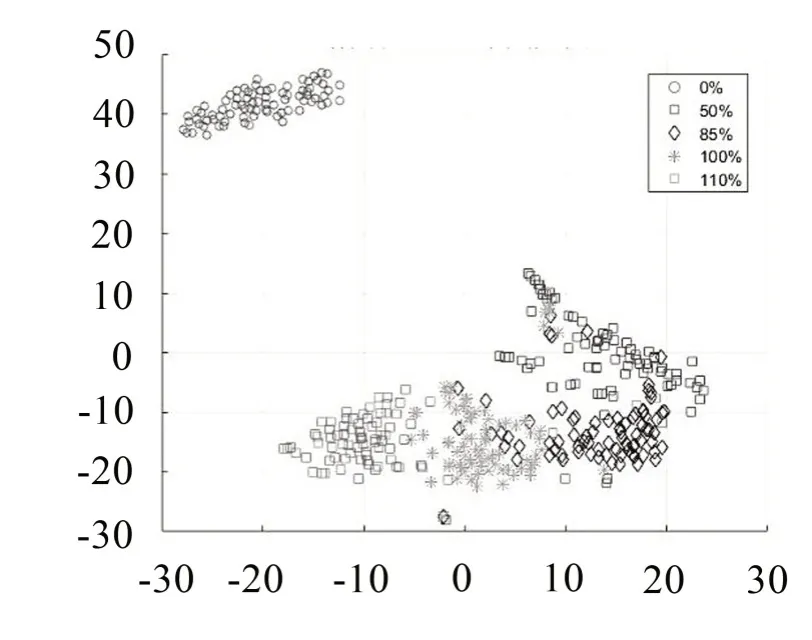
图9 t-SNE算法二维映射降维结果
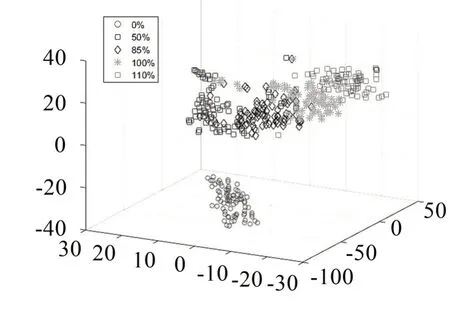
图10 t-SNE算法三维映射降维结果
图9和图10分别为某20 缸柴油机五种负荷状态的特征向量样本和测试数据集经过流形学习t-SNE算法降维至二维和三维的结果,其中0%负荷的数据点离其他四种负荷数据点较远。50 %,85%,100%,110%的数据点集之间的界限明显。
之后使用KNN算法对测试数据点进行识别,将K值的区间设定为5~20,分别计算不同K值的KNN识别率。由表4和表5显示,二维情况下,K值为6时,各工况平均识别率94.15%最高;三维情况下,K值为7 时,各工况平均识别率94.16%最高。因此,在二维时选择K值为6 的KNN 进行识别;在三维时选择K值为7的KNN进行识别。
3.2 与其他方法的对比与分析
为了进一步验证本文方法的有效性,利用20缸大型柴油机监测数据,对比应用了主成分分析(PCA)方法、BP 神经网络方法处理上述数据,结果如下所示。
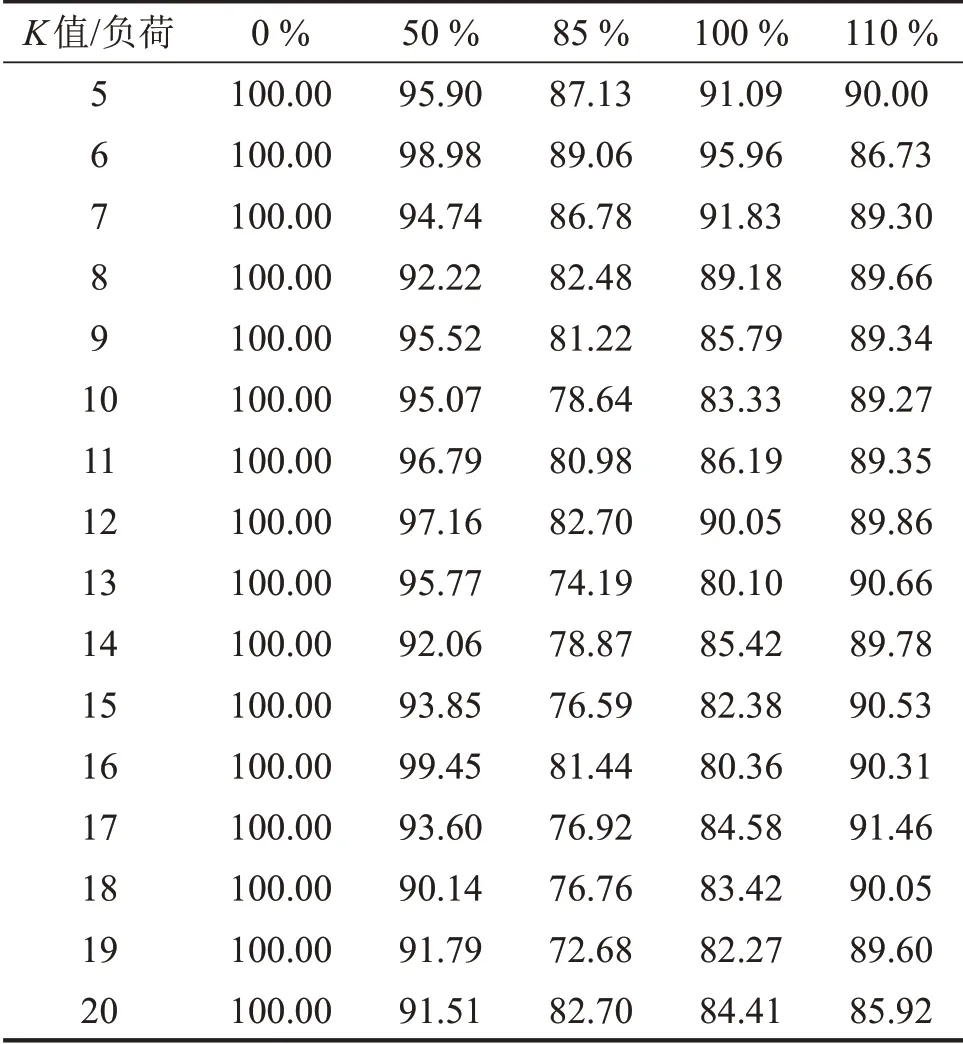
表4 二维映射下不同K值KNN识别率/(%)
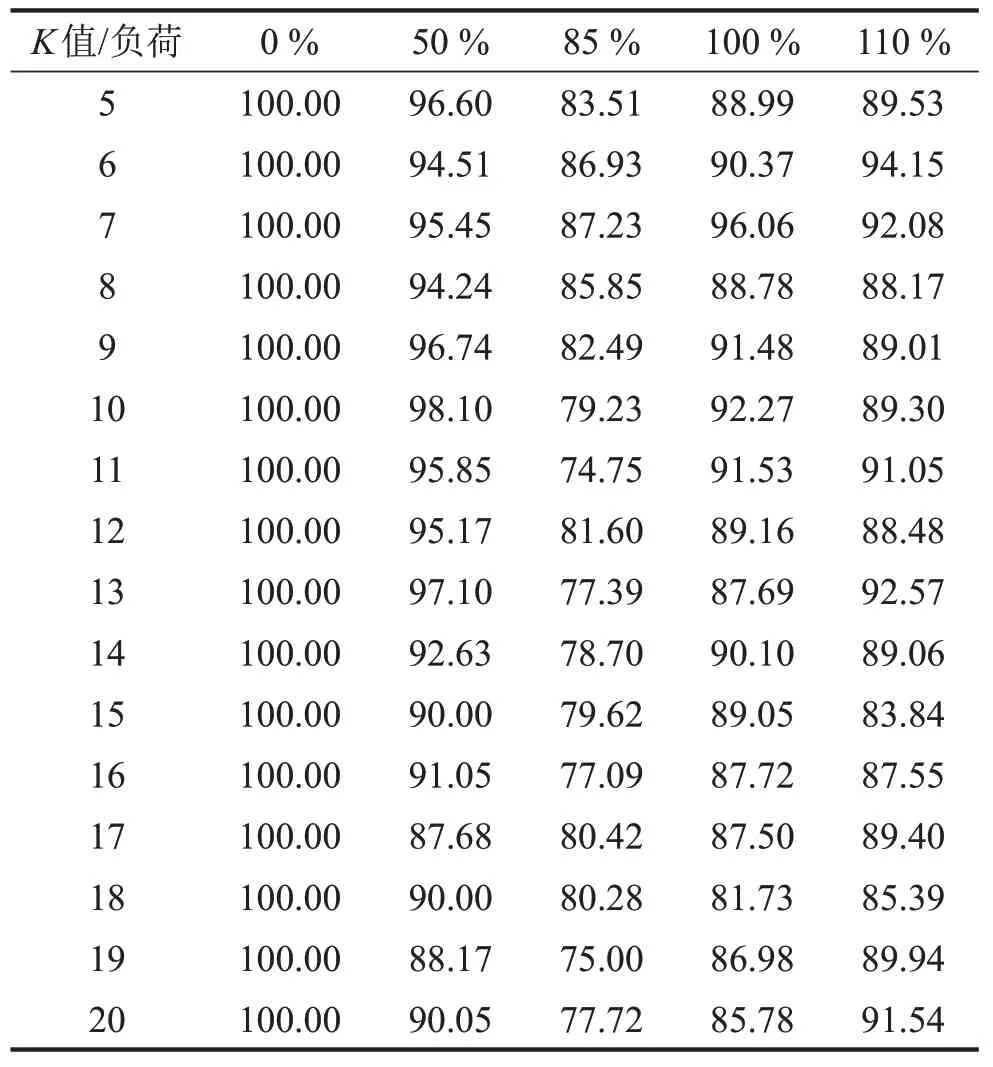
表5 三维映射下不同K值KNN识别率/(%)
图10和图11分别为某20 缸柴油机5 种负荷状态的特征向量样本和测试数据集经过PCA 算法降维至二维和三维的结果。数据经过PCA降维后,从数据分布看,数据混淆的程度比t-SNE严重。
图13为二、三维的BP 和KNN 算法的5 种工况识别率比较图。
从上述结果中,可看出:
(1)t-SNE 算法比PCA 方法在数据降维和聚类效果上具有优势;
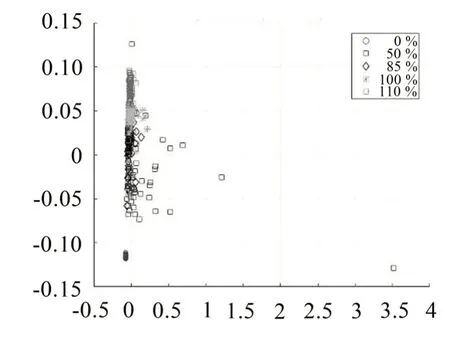
图11 PCA算法二维映射降维结果
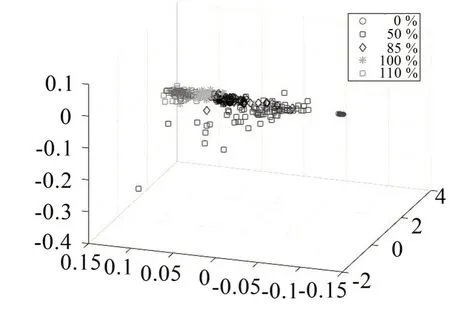
图12 PCA算法三维映射降维结果

图13 BP神经网络与KNN算法分类结果比较
(2)针对本文20缸柴油机数据样本,KNN算法对柴油机运行工况识别效果优于BP神经网络;
(3)数据特征向量降维至三维的工况识别率优于二维,因此合理选择降维维度对提高分类准确度有重要作用。
4 结语
本文提出了一种基于流形学习和KNN 算法的柴油机工况识别方法,提取了对工况敏感的特征参数,组成特征向量,使用流形学习t-SNE算法对特征向量数据降维,最后进行KNN算法工况识别。利用不同机组数据验证了方法的实用性;并针对气门故障条件下的柴油机运行状态识别开展了研究。
得到的结论如下:
(1)基于流行学习和KNN 算法的柴油机工况识别方法对正常状态下的机组运行状态具有较高的识别准确率;
(2)柴机油故障对工况的识别产生了不利影响,降低了识别准确性,但是总体仍达到了较好的识别准确率。后续将针对故障特征与负荷状态特征进行深入研究,一方面提高柴油机工况识别准确度,另一方面为变负荷工况故障监测诊断奠定基础。
