不同耦合模式水下结构声辐射计算方法研究

2019-06-25蒋坤，向阳，张波

噪声与振动控制 2019年3期

蒋坤，向阳，张波

（ 1.武汉理工大学高性能船舶技术教育部重点实验室，武汉430063；2.武汉理工大学能源与动力工程学院，武汉430063；3.船舶动力系统运用技术交通行业重点实验室，武汉430063）

随着现代声呐探测能力的不断进步，对于潜艇的声隐身性能提出了更高的要求。而提高潜艇声隐身性能的最重要的措施就是主动降低和隐蔽自身的辐射噪声，因此研究水下结构的辐射声功率及声振特性具有重要意义。潜艇的水下辐射噪声源主要有：振动激励下传递到外壳体引起水下声辐射的结构噪声；螺旋桨转动激发的振动辐射噪声和空泡噪声；潜艇处于前进状态时水流激发的流噪声。另外，潜艇水下辐射噪声源的频率范围广，且由于其发生的环境为固体结构和周围流场交互的复杂环境中，涉及到流固耦合与声固耦合等诸多振动与声学问题，因此需要根据潜艇所处环境以及频率的划分，建立合适的声振数值分析模型，并进行相应的数值计算方法求解。

李清[1]和冯娜[2]归纳了几种水下结构低频声辐射的数值计算方法，并比较了各种方法的计算特性；张波[3]和袁自强[4]基于有限元/边界元混合法和统计能量法对水下加肋圆柱壳进行了全频段的声振特性研究；和卫平[5]和R.S.Langley[6]基于统计能量理论作了研究，其中和卫平证明了利用统计能量法进行圆柱壳中、高频振动与声辐射研究的可行性，R.S.Langley 提出一种基于模态叠加法及模糊结构机理并结合统计能量理论的结构振动响应分析混合方法；Jing Tang XING[7]、LUIS R[8]和F Kalateh[9]对流固耦合数值计算方法作了研究，其中Jing Tang XING比较了线性与非线性流固耦合动力学数值方法，并阐述了2 种类型数值方法的进展及应用，LUIS R 基于有限元方法建模及边界元方法表示声学线性流体的方法研究了声学流固耦合作用问题中的2个有限元-边界元耦合公式。F Kalateh 研究了流体与结构耦合动力学方程时间积分的2 种不同划分求解方法，详细说明了求解过程，并以各种计算实例比较了2种求解方法的差别。

由上可知，国内外学者基于不同的方法对结构的全频段声振特性做了研究，但对结构与流体在不同耦合模式下的声学特性研究还鲜有涉及，而本文将针对中低频0～200 Hz 频段计算水下双层加肋圆柱壳的声辐射，对比基于流固耦合和声固耦合2 种计算方法的理论及结果的异同，以期为水下结构的声辐射研究提供参考。

1 理论概述

1.1 基于流固耦合的FE-IBEM混合法

该方法的基本思想是：在流场与结构之间建立耦合动力学方程，并在此基础上通过有限元方法计算结构的振动物理量，如结构的振速与位移，之后将计算得到的结构外表面的振动响应结果作为声辐射计算的边界条件，在声学软件中利用间接边界元求解器计算各声学量，如辐射声功率，声压。

工程上应用流固耦合模式计算低频水下辐射噪声时，在计算结构振动响应这一步时通常把流体简化为理想、无旋、不可压缩的流体，这种简化忽略了水作为可压缩性流体对结构振动引起的阻尼效应，因此流体对于结构的影响仅表现为附加质量，此方法存在一定误差，但应用在低频的工程问题上仍在误差范围内，通过上述简化，有如下描述流体运动的公式

式（1）为无旋假设下满足的条件，即流体速度等于速度势函数的梯度，式中v为流体速度，φ为流体的速度势函数，。式（2）为将式（1）代入不可压缩流体的连续性方程得到的拉普拉斯方程。结构和流体经有限元离散化，得到如下描述流体与结构耦合的耦合动力学方程

式中：KS、CS和MS分别为刚度矩阵、阻尼矩阵和质量矩阵，u为结构的节点位移，ω为耦合系统振动频率，M'S为由于流体的耦合产生的附加质量矩阵，FS和F'S分别为结构所承受的外载荷和流体激励所产生的流体动力矩阵。求解上述有限元耦合方程获得的结构外壳响应振速，最后以法向速度的形式作为边界元方法求解的初始条件，代入边界元方程组求解得到声压及辐射声功率。

1.2 基于声固耦合的FE-IBEM混合法

声固耦合模式下的FE-IBEM 混合法基本思路为：首先建立结构有限元模型和结构表面的边界元模型，通过有限元方法计算结构整体干模态，将计算后的干模态和结构湿表面边界元模型导入统一的声学间接边界元求解器中，再加上载荷形成结构与流体的声固耦合分析模式，通过声振耦合计算得到相应的响应结果。

声固耦合模式下求解的耦合方程与上述流固耦合求解的耦合方程基本一致，所不同的是，该分析模式下输入载荷进行结构振动分析和利用间接边界元法进行声场分析是同步进行的，这个过程中把流体考虑为可压缩性流体，此时流体用式（4）描述

式中：k=ω/c，ω为频率，c为介质中声速（论文研究介质为海水）。对比式（2）与式（4）易知当频率ω较小时，k2φ的值较小，2个控制方程解出来的值近似，说明此时流体为可压缩或不可压缩对研究结果影响不大；而当频率ω较大时，k2φ值较大，两个控制方程解出来的值不再近似，流体可压缩与不可压缩对研究结果的影响将凸显。声固耦合模式中，系统的耦合动力学方程[1]如下

式中：Ka、Ca和Ma分别为流体刚度矩阵、阻尼矩阵和质量矩阵，ρa为流体密度，Fa为声场激励载荷向量，为声固耦合矩阵。流体对结构的影响体现在通过对耦合动力学方程同时求解上，从而流体对结构振动的影响既表现为附加质量也表现为阻尼效应耗散能量，即充分考虑了流体对结构的耦合作用，通过求解上式耦合动力学方程，再经换算得到辐射声功率。另外声固耦合模式在建模方法上较简单，不需要建立庞大的有限元流体域，而通常采用边界元离散建立流体域。

2 双层加肋圆柱壳水下声辐射计算

计算所采用的双层圆柱壳外径为8 m、内径为7 m、壳长为11 m，壳体内部全为空气，内外壳之间采用环形肋板，沿母线方向以间隔0.5 m的距离横向排列，外壳两端有封闭的端面以保证约束。内外壳、端面与肋板的厚度均为0.036 m。整个结构材料均为钢材，密度为780 kg/m3，泊松比为0.3，杨氏模量为2.1×1011Pa。激励为100 N的简谐力，作用在内壳中心位置，方向为垂直母线向外，辐射的介质为海水，25°C 海水中声速为1 500 m/s，密度为1 025 kg/m3。如图1为双层加肋圆柱壳模型示意图。

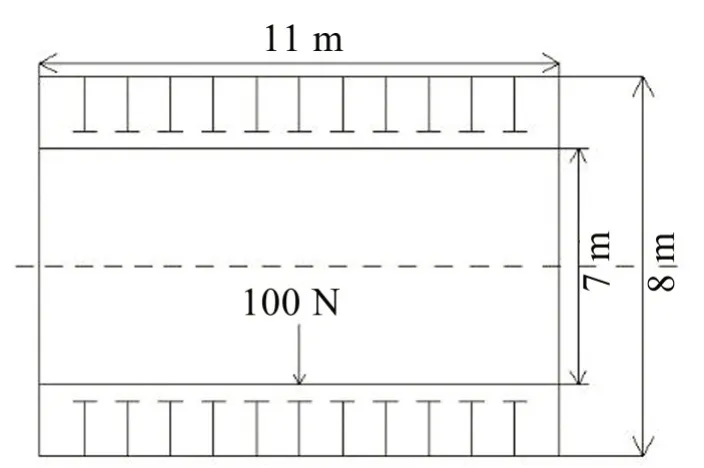
图1 双层加肋圆柱壳模型示意图

2.1 基于流固耦合模式的水下声辐射

该模式下弹性圆柱壳浸没在无限域流体中，因此需要建立双层圆柱壳结构模型和流体单元模型，建模过程均在HyperMesh 中完成，其中结构为板壳结构，外壳及端面由于跟流体直接接触，采用shell63单元来模拟，内壳与肋由于没有跟流体直接接触，采用shell181 单元来模拟，结构网格尺寸需满足一个波长内有6～8 个单元，因此结构网格尺寸实取0.16 m。由于双层圆柱壳浸没在水下较深处，截断流体采用fluent30 单元模拟的一个包围结构的有限大小的流体球，且为了保证流体单元导入ANSYS计算时产生准确值，流体截断半径Rf应满足[11]

式中：λ为需要计算的下限频率对应的主波长，r为外壳半径，根据此公式截断流体球的半径取为19 m。除此之外，为便于外壳和与之相接触那部分流体之间的节点耦合，建立一个包络双层圆柱壳的过渡流体圆柱，过渡流体圆柱与双层圆柱壳中心和母线方向相同，长度为13 m，半径为5 m，过渡小圆柱的流体网格尺寸取为0.16 m，空心流体球网格尺寸为提高计算效率实取0.5 m。如图2所示为整个双层圆柱壳结构和流场剖视图。

图2 双层圆柱壳结构与流场剖视图

将上述建好的模型导入ANSYS，对外壳和与之接触的那一层流体施加流固耦合作用（FSI），经FSI作用后，在双层圆柱壳与接触的流体之间建立了动力学耦合方程，在此基础上施加100 N 的简谐激励力，计算结构在0～200 Hz 频率范围内且步长为2 Hz的耦合振动，再将计算所得外壳的振动数据作为水下声辐射计算的边界条件，导入LMS Virtual.Lab，建立起声学响应计算模型，采用间接边界元求解器计算声学物理量，同时为分析流体负载对声辐射计算结果的影响，将空气介质中的声压响应与水中声压响应作对比，得到声辐射和声压结果如图3所示。

由图3（b）可以看出在0～110 Hz，结构在水中的辐射声功率先随着频率升高而增大，在频率110 Hz以后，围绕某一平均值上下波动，且在178 Hz 达到频段内的最大值为97.75 dB，频段合成声功率为99.29 dB；由图3（c）、图3（d）可知，结构在水中和空气中的声压曲线整体趋于平缓，但水中的声压明显大于空气中的声压，这是由于水的密度及声音在水中的传播速度远大于空气，使得水中的声阻抗远大于空气，从而导致水中声压大于空气中声压，且由于声功率级与声压级正相关，因此水中的声功率级也大于空气中的声功率级，以上均表明结构声辐射的大小与辐射介质的阻抗特性有关。展示峰值频率136 Hz与178 Hz的场点声压云图如图4所示。

图3 流固耦合模式

图4 峰值频率处声压云图（流固耦合模式）

结果表明频率136 Hz 处声压最大值在双层圆柱壳端面，而频率178 Hz处声压最小值在双层圆柱壳端面，最大值在圆柱壳侧面。

2.2 基于声固耦合模式的水下声辐射

声固耦合模式计算时需要对模态进行截断，为提高计算效率同时保证计算精度，需要选择合适的模态截断阶数。对不同模态截断数下的圆柱壳结构，在同样位置加上100 N的简谐力，频率为0～200 Hz，计算截断模态下的平均输入功率，计算结果如表1所示。

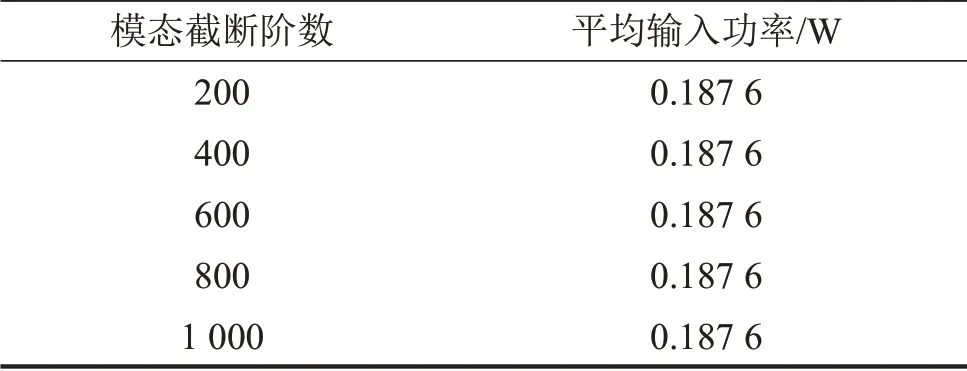
表1 不同模态截断数下带宽输入功率

各模态截断数下带宽输入功率相等，证明对于本文所研究的结构较简单的圆柱壳，模态截断阶数不小于200 时对声辐射计算结果几乎没有影响，因此为提高计算效率，截取前200阶模态即可。

在ANSYS中计算结构在真空中的干模态，提取前200阶模态，计算频率范围为0～200 Hz，如图5所示。为结构在真空的几个典型模态。同时为说明流体对结构的附加作用使模态固有频率产生变化，计算了结构在流体中的前200阶湿模态[10]，展示与干模态振型一样的几阶湿模态振型如图6所示。对比图5与图6可以看出，由于流体的附加作用，使得相同振型的湿模态固有频率变小。

将结构干模态和外壳边界元网格导入LMS Virtual.Lab，建立起结构和声场的声固耦合模型，在内壳同样位置施加100 N 的简谐力，采用基于模态叠加法的间接边界元求解器进行声振耦合一体化计算分析。计算模型与计算结果如图7所示。

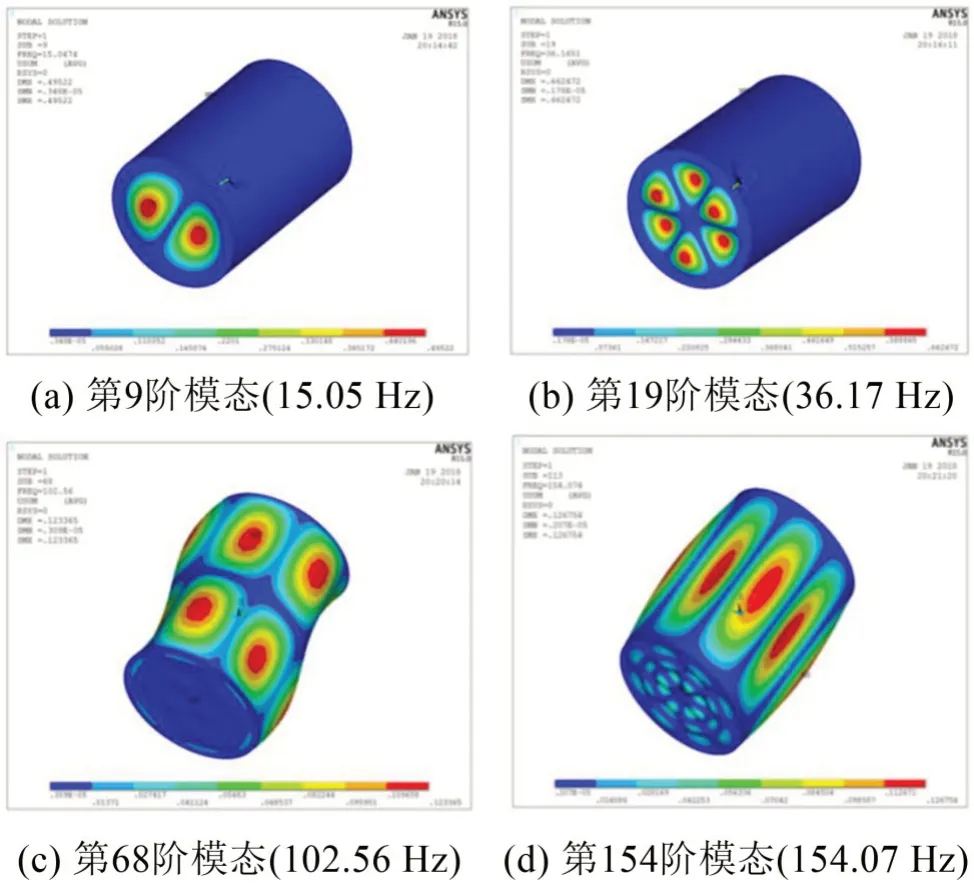
图5 结构在真空中的几个典型模态

由图7（b）可知结构声辐射在0～88 Hz 整体随频率增加而增大，之后围绕某一平均值上下波动，且在频率88 Hz与192 Hz处存在两个明显高于其他频率处的峰值，研究频段内的合成声功率为94.81 dB。

图6 结构在流体中的几个典型模态

由图7（c）与图7（d），并对比流固耦合模式计算结果图3（c）、图3（d）可得，同样位置的场点1与2处的声压整体比流固耦合模式小（A计权后，流固耦合模式水中场点1 合成声压102.67 dB、场点2 合成声压111.16 dB，声固耦合模式水中场点1 合成声压92.00 dB、场点2 合成声压98.46 dB），水中声压仍然高于空气中声压，再次验证结构辐射噪声与流体阻抗特性有关。展示峰值频率88 Hz与192 Hz处的场点声压云图如图8所示。

频率88 Hz 处声压最小值在圆柱壳端面，其余大部分位置处于较高值，频率192 Hz处声压最小值位于圆柱壳外面垂直于激励力的圆柱壳中剖面上。

图7 声固耦合模式

图8 峰值频率处的声压云图（声固耦合模式）

2.4 两种耦合模式计算结果综合分析

流固耦合模式与声固耦合模式两种标准数值方法计算得到的声功率值如图9所示。

图9 两种标准数值计算方法对比

由图可以看出，整体趋势上，2 种耦合模式辐射声功率值随频率增加差距逐渐变大。到80 Hz 以后，除个别数据点外，流固耦合模式声功率值明显大于声固耦合模式声功率值。这与1.2 节中所述2 种耦合模式下流体控制方程在高低频求解时呈现的差别一致，即低频求解的值近似，中高频求解的值差距较大。

基于统计能量法计算结构带宽内模态数如图10所示。由图可以看出，在频率小于12.5 Hz 时，结构所有组成部分模态数均小于1，因此0～12.5 Hz可以划分为结构的低频区；在频段12.5 Hz～200 Hz，内壳及环肋部分的模态数小于5，外壳及端面部分的模态数大于5，则12.5 Hz～200 Hz属于结构中频区[12]。

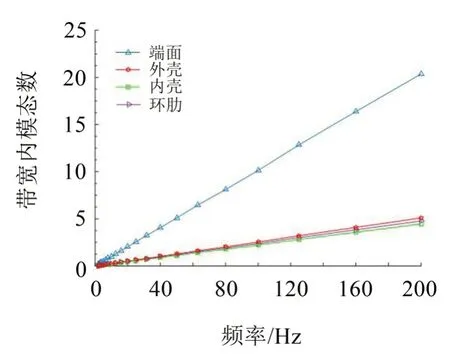
图10 双层圆柱壳结构带宽内模态数

以声固耦合模式声功率值为基准，计算2 种耦合模式声功率平均相对误差，得到0～12 Hz 为4.85%，0～14 Hz为5.65%。以5%的相对误差为界限，则可认为0～12 Hz 2 种耦合模式计算结果近似，定义为结构低频段。此后随频率增加，除个别数据点处，平均相对误差越来越大，12 Hz～200 Hz 2种耦合模式声功率平均相对误差达到23.53%，远大于5%，属于结构中高频段。

由上分析可以看出，通过相对误差分析划分的低频区基本与统计能量法划分的低频区一致。则由控制方程式（2）与式（4）推出的定性结论：2种耦合模式低频求解结果近似，中高频求解结果差距较大，转为了本文算例中更为具体的定量结论：2种耦合模式低频0～12 Hz 求解结果近似，中频12 Hz～200 Hz求解结果差距较大。

另外，流固耦合模式和声固耦合模式带宽内合成声功率分别为99.29 dB 和94.81 dB。从声功率结果和相同场点的声压结果看，流固耦合模式均大于声固耦合模式，这是由于流固耦合模式忽略了流体的可压缩性，而这种可压缩性引起的阻尼效应耗散能量随着频率的增加越发明显，从而导致流固耦合模式比声固耦合模式耗散能量少，流固耦合模式计算结果逐渐高于声固耦合模式。在计算频段内，流固耦合模式和声固耦合模式2种标准数值计算方法合成声功率级相差仅为4.48 dB，尽管从数值结果上无法确定哪一种结果更加接近真实值，但从2 种模式的理论推导来看，显然声固耦合模式把流体对结构的影响考虑得更合理，计算结果更接近真实值。

3 双层圆柱壳肋板声学特性研究

肋板对双层圆柱壳的水下声辐射有着重要的影响，不仅提高了结构的强度和稳定性，而且作为连接内外壳的桥梁起着传递振动能量的作用。为研究肋板间距与厚度对结构水下声辐射的影响，基于声固耦合模式计算不同肋板间距与厚度下的声学响应，根据模型大小，设置肋板间距分别为0.4 m、0.5 m和0.6 m，并计算结构单位长度内的肋板个数如表2所示。研究肋板厚度分别为0.032 m、0.036 m 和0.04 m。计算结果如图11所示。

表2 不同肋板间距下单位长度肋板个数

图11 不同间距和不同厚度肋板的辐射声功率

由图11（a）可以看出，在所研究的频段范围内，2 Hz～50 Hz之间不同间距肋板的声辐射没有太大差距，但在频率50 Hz 之后，3 种间距肋板的辐射声功率有明显差异，在频率56 Hz处0.6 m肋板间距的双层圆柱壳存在一个远高于0.4 m和0.5 m间距的峰值，在频率84 Hz 之后3 种间距辐射声功率趋于平稳，0.5 m肋板间距的辐射声功率整体大于其他2种间距，但3 种肋板间距合成声功率相差不大，0.4 m、0.5 m 和0.6 m 间距的辐射声功率分别为91.76 dB、94.81 dB和92.11 dB，结合表2与图11（a）知，在本文研究的结构中，单位长度肋板个数为26/11比单位长度肋板个数为21/11 和17/11 时的辐射声功率都要小，这是因为此时单位长度肋板个数最多，使得整个结构刚度最大，相对不容易产生变形，因此振动及声辐射较小。综合以上情况，考虑合成声功率值及辐射声功率随频率变化的峰值情况，对于所研究的3种单位长度肋板个数，可选择单位长度肋板个数为26/11，不仅使得结构的辐射声功率在低频0～100 Hz 没有很高的峰值，也让结构的合成声功率值最小。

由图11（b）可知，在频段2 Hz～76 Hz内，3种肋板厚度对应的辐射声功率曲线基本重合，说明在2 Hz～76 Hz 频段内，肋板厚度对双层圆柱壳的辐射声功率影响不大，但在频率76 Hz 以后，3 种厚度肋板的计算结果差异显现，肋板厚度为40 mm 的辐射声功率曲线整体起伏不大，且声功率值基本低于其余2 种肋板厚度，肋板厚度为32 mm 的辐射声功率曲线出现2 个明显的峰值，肋板厚度为36 mm 的双层圆柱壳在192 Hz出现一个明显高于其他2种肋板厚度的峰值，32 mm、36 mm和40 mm厚度肋板对应的合成辐射声功率分别为97.23 dB、94.81 dB 和90.13 dB，可以看出总体上随着肋板厚度的增加，辐射声功率减小，且辐射声功率曲线波动幅度变小。