具斑块迁移的病毒模型的稳定性分析

柳文清,陈清婉

(福建师范大学闽南科技学院,福建 泉州 362300)

1 引言

近年来,病毒型疾病暴发愈加频繁,使得研究病毒机制成为十分热门的课题.一般的病毒感染过程可用如下模型[1-4]:

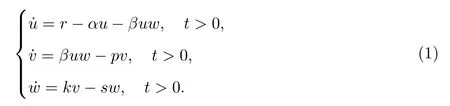
其中u,v,w分别表示未感染细胞,感染细胞及游离病毒.其中未感染细胞以常数率r生成,以速率αu死亡,以速率βuw成为被感染细胞,其中β是描述感染过程的常数率,相当于未感染细胞与游离病毒的接触率.被感染细胞以速率βuw生成,以速率pv死亡.游离病毒由被感染细胞死亡裂解而产生,其速率为kv并以速率sw被清除.由一个被感染细胞内产生的病毒颗粒的总数为.

上述模型假设空间分布均匀且未感染细胞与感染细胞的感染关系是线性的.这并不能完全描述比较复杂的实际情况.文献[5-7]引入了B-D反应函数来描述未感染细胞与感染细胞的感染关系.文献[8]则考虑病毒的空间迁移效应,即如下模型:

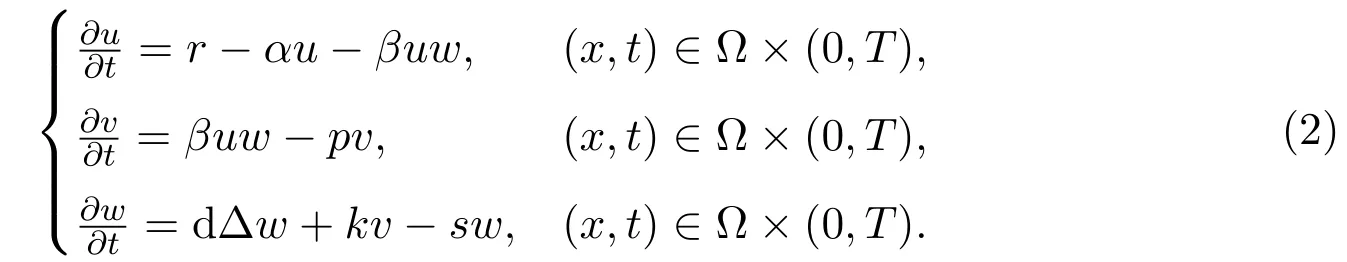
文献[9-10]则进一步考虑未感染细胞,感染细胞和游离病毒均可自由迁移的情形,即在模型(1)中等式右边分别加上d∆u,d∆v,d∆w表示迁移.

另外,考虑到病毒容易传播的性质,很多学者考虑了斑块环境下的病毒模型和传染病模型[11-14].文献[14]讨论了一类基于斑块和人口流动的传染病模型,即

证明了病毒趋于灭绝的条件和地方病流行的条件.受此启发,本文研究如下具有斑块迁移的病毒模型:

其中ui,v,i=1,2分别表示第i个斑块上未感染细胞,感染细胞,ei,i=1,2分别表示未感染细胞在斑块间的传播率.可以理解为携带这些细胞的主体的迁移,例如禽流感病毒的传播等.记N(t)=u1+u2+v,K=min{α1,α2,p},将方程组 (4)中前四个方程相加,得,由常微分方程比较原理可得,再由,同理可得.另外方程组中前两个方程同时也满足

本文主要在区域G上讨论模型(4)的相关性质.

2 无病平衡点的稳定性分析

当R>1 时,模型 (4)存在地方病平衡点并且满足

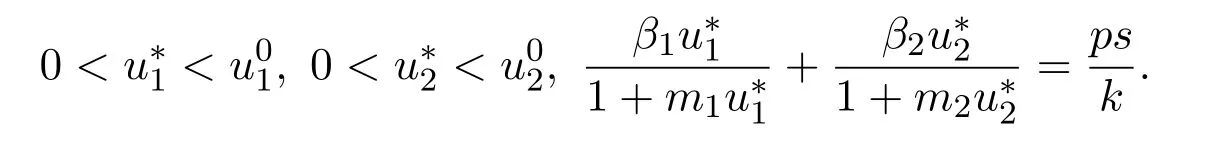
为下文证明需要,不加证明的给出以下引理.

引理2.1(LaSalle不变集原理)设V是方程x˙=f(x)定义在D上的Lyapunov函数,若M是方程x˙=f(x)在E中的最大不变集,且x有界,则x(t)→M,当t→∞时.

定理2.1若R<1,则模型(4)的无病平衡点E0在域G上是局部渐近稳定的.

证明模型(4)在无病平衡点E0处的线性化系统的特征方程为:

定理2.2 当满足条件R<1并满足条件:,模型(4)的无病平衡点E0在域G上是全局渐近稳定的.

证明模型(4)的等价系统为:

当R<1时,上述特征方程的根均有负实部.故平衡点E0是局部渐近稳定的.

当R>1时,上述特征方程中至少有一特征根为正,此时E0是不稳定的.

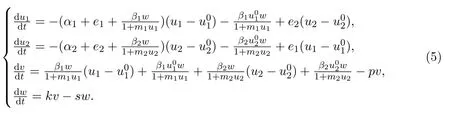
由定理的条件可知D+V(t)≤0.可见,集合

是系统(5)的最大不变集,由LaSalle不变集原理可知无病平衡点E0在域G上是全局渐近稳定的.对任意的初值(u10,u20,v0,w0)∈G,有

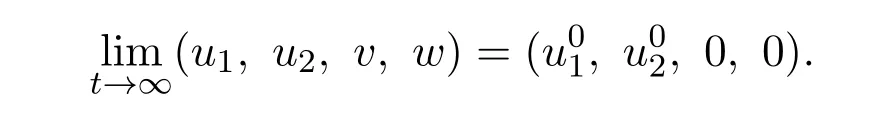
3 地方病平衡点的稳定性分析

定理3.1当满足条件R>1时,模型(4)的平衡点E∗在G上是局部稳定的.

证明模型(4)在无病平衡点E∗处的线性化系统的特征方程为:

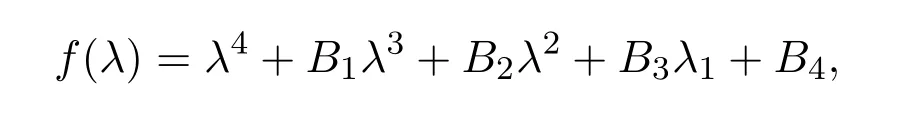
其中B1=p+s+a11+a22,B2=a11a22−e1e2+(a11+a22)(p+s),

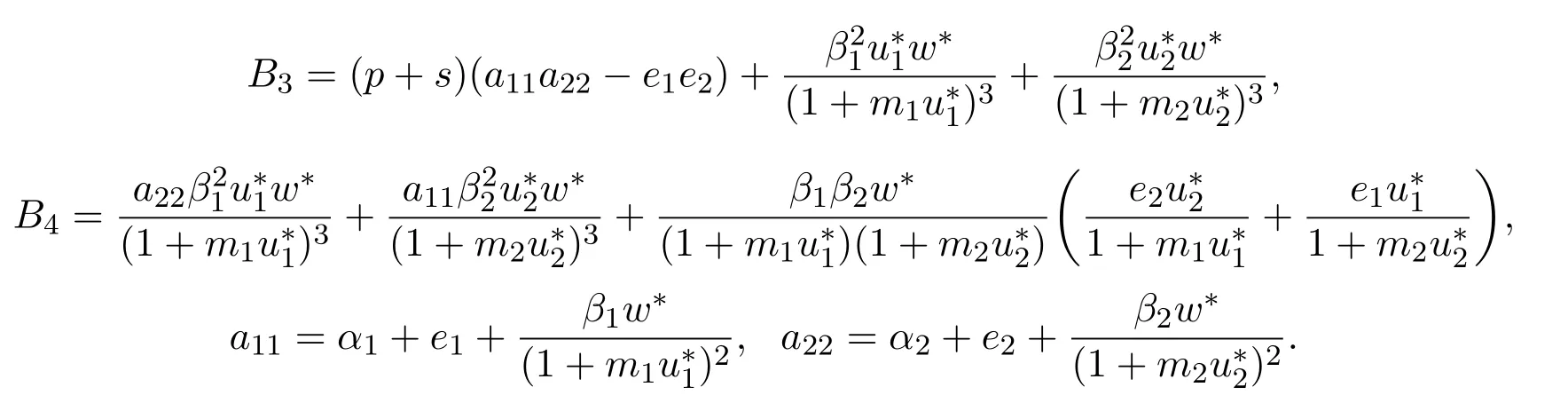
由于f(0)=B4>0,并且f′(λ)=4λ3+3B1λ2+2B2λ+B3>0.这说明f(λ)=0 无正实根,下面说明f(λ)=0无纯虚根.假设λ=iω(ω>0)是特征方程的特征根,代入方程,则有 (ω4−B2ω2+B4)+i(B3ω−B1ω3)=0,由上式可得

定理3.2 当满足R>1并且满足条件,模型 (3)的地方病平衡点E∗在域G上是全局渐近稳定的.

证明模型(3)的等价系统为:

由定理的条件可知D+V2(t)≤0.可见,集合

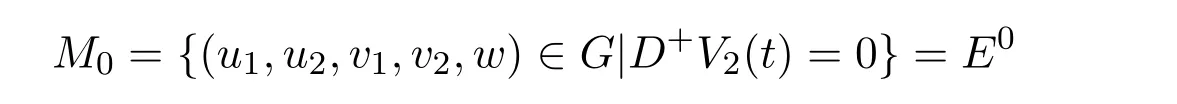
是系统(6)的最大不变集,由LaSalle不变集原理[16]可知无病平衡点E0在域G上是全局吸引的.对任意的初值(u10,u20,v0,w0)∈G,有

4 结论

本文定理2.2和定理3.2表明,阈值R<1时,感染细胞生成病毒的速度相对小而病毒细胞死亡率足够大,斑块迁移率较小时,病毒趋于灭绝;而阈值R>1且感染细胞生成病毒的速度相对大而病毒细胞死亡率足够小,斑块迁移率较大时,病毒持续流行.