基于迭代正则化高斯-牛顿法的非线性Urysohn积分方程数值解

陈亚文,仝云莉,闵涛

(西安理工大学理学院,陕西 西安 710054)

1 引言

在物理学、力学和工程技术诸多领域都存在大量的非线性不适定问题,例如参数识别问题、逆散射问题、逆位势问题以及第一类Fredholm积分方程求解问题等[1].这类问题一般归结为求解下面的非线性不适定算子方程:

其中,F:D⊂X→Y是定义域为D的非线性算子,X,Y为Hilbert空间.当(1)式的解不连续依赖于右端数据y时,称(1)式为不适定的.在实际问题中,右端数据y通常是由测量得到的,因而得到的数据是一个满足∥yδ−y∥≤δ的近似数据yδ,这里δ>0是给定的很小的扰动水平[2-4].

一个典型的例子就是Urysohn型非线性算子方程[5]:

这里x(s)未知,K(t,s,x(s))为定义在 [a,b]×[a,b]×R上的核函数,且非线性依赖于x(s).

由于上述问题的不适定性,为了获得稳定的、准确的数值解,就必须使用正则化方法.本文利用迭代正则化高斯-牛顿法求解问题(1)或问题(2).此外,采用Sigmoid-型函数确定正则化参数,由于Sigmoid-型函数的性质,随着迭代次数的增加,函数值不断减小并逐渐趋于0,以此来确定一个最佳的正则化参数.

2 迭代正则化高斯 -牛顿法

设方程(1)有解x∗(不必唯一),yδ是y的扰动,

如用牛顿法求解方程(1),则由线性化方程

确定xk+1.一般情况下,F′是不可逆的,需要通过正则化方法来求得其解x∗的近似.

为此,可定义泛函

其中,α>0为正则化参数,Ω(x)为先验条件.要求无约束最优化问题(5)的解,首先将算子F线性化,利用F(x)在第k次迭代点xk处的泰勒展开式,得到

其中Ω(x)=∥L(x−x0)∥为稳定泛函,L是单位矩阵(L=L0=I∈Rn×n)或者是一阶算子的离散近似,即 [L1]ij=δi,j−δi,j−1,i=1,2,···,n−1,其中,δi,j为克罗内克符号,j=1,2,···,n,方程(6)通过一阶最优条件求解,可得到:

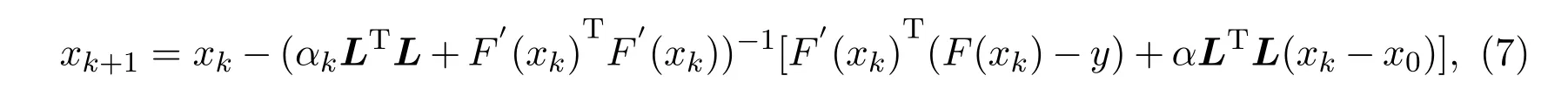
(7)式称为迭代正则化高斯-牛顿法[6-7],简记为IRGN法.αk表示正则化参数且为单调递减序列并满足:

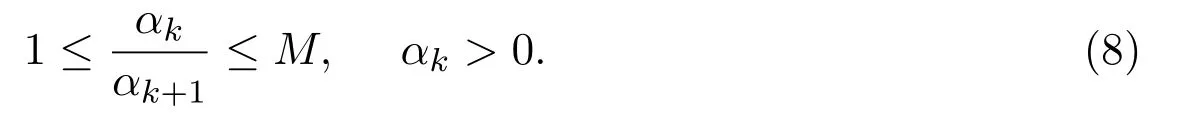
正则化参数的选取规则(8)是保证正则化方法收敛的必要条件,即当扰动水平趋于0时,正则解收敛到真解.有关此迭代算法的收敛性定理的证明可参考文献[8-12].

3 离散化

为了数值求解(2),需要将其离散化,离散化的方法有很多,这里采用梯形公式进行离散.将(7)式改写为如下形式:

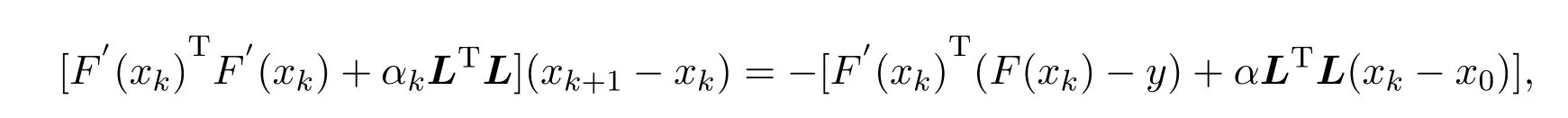
要得到F′(xk)TF′(xk),需要求解非线性算子F的 Fréchet导数.

令K(t,s,x(s))为定义在a≤t,s≤b,|x|≤r上的函数,并设

处处连续.积分算子F为[a,b]上的连续函数,并且在开球上Fréchet可导,对任意的x0∈C[a,b]且,h∈C[a,b],可得到F的 Fréchet导数为:

上述(9)式定义的算子是[a,b]上的线性连续算子.

事实上,对于确定的θ=θ(h)∈[0,1],有

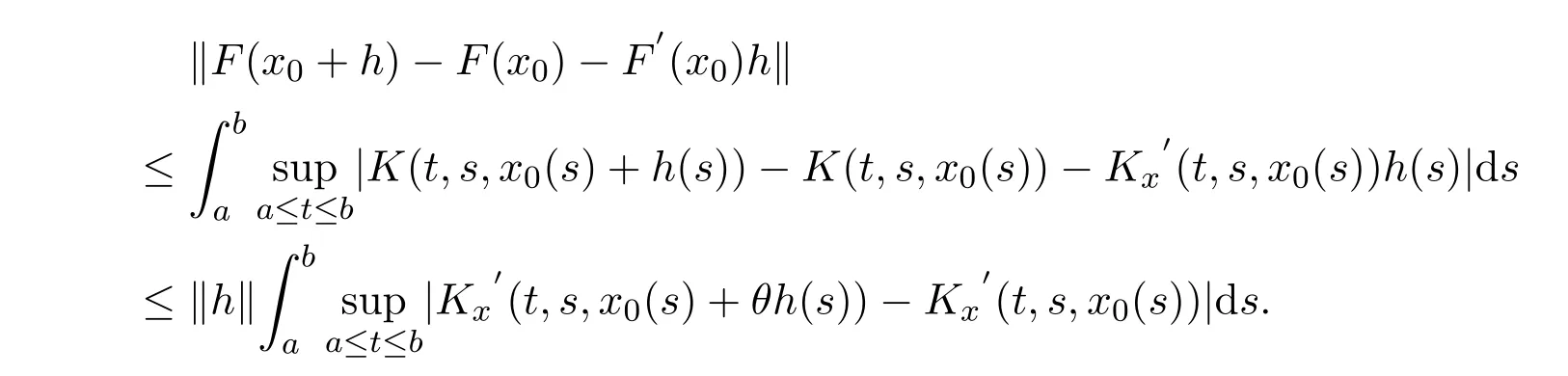
因此F的Fréchet导数可以通过(9)式得到.

利用梯形公式将方程(9)进行离散:把区间[a,b]等分成N个小区间,其步长为

令s0=a,sj=a+j△s,同理

设x(sj)=xj,则有

改写成矩阵形式为:

其中

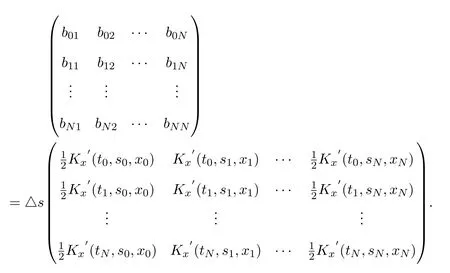
利用迭代正则化高斯-牛顿法可得到:

其中

因此得到迭代格式x(k+1)=x(k)+h(k),通过此格式便可求出(2)的近似解.

实现上述算法的关键在于选择合适的正则化参数αk.本文基于Sigmoid-型函数的性质,按如下方法选取正则化参数:按照(11)式选择的正则化参数,不难验证其满足下列条件:

可以看到,根据上述正则化参数的选取方法,在迭代开始时能够充分对问题进行正则化,然后随着迭代数的增加正则化参数逐渐减小,达到解稳定的目的.

4 数值模拟

考虑重力测定中的一个实际问题[13-15].它在地球物理反演中经常遇到,是一个典型的研究问题.设有一物体,其密度与环绕其周围的介质的密度不同.问题是通过测定由于重力场作用产生的隅角来判断物体的形状.

假设地面下 (z=0)介质的密度分布不均匀,为简单计,设有两种密度分布ρ1和ρ2,它们被一边界z(x)隔开(见图1).

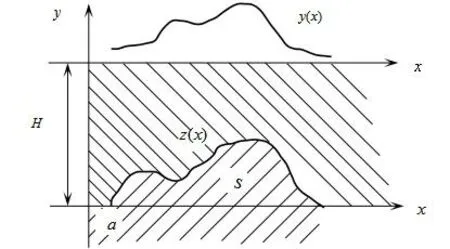
图1 重力测定原理图

在如此的设定下,由于重力场的作用,可以在地表测得一隅角为其中V是由于密度差ρ=ρ2−ρ1引起的位势.

而隅角∆g是可以测定的,于是问题就是要确定边界z(x).这就化归为求解如下的非线性Urysohn积分方程:

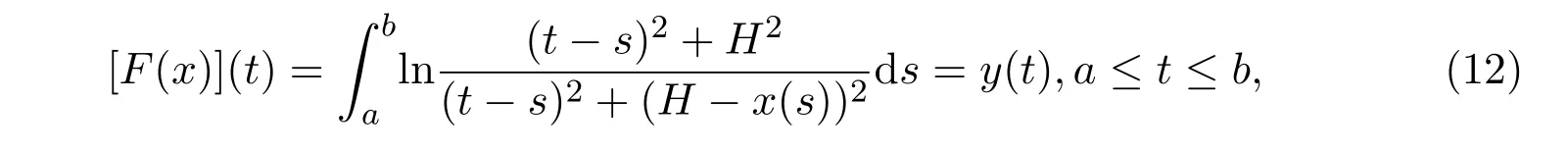
其中F是一个非线性算子.

在数值求解之前,先做如下规定:

1.用L∞表示误差范数,即

2.用RE表示相对误差,即

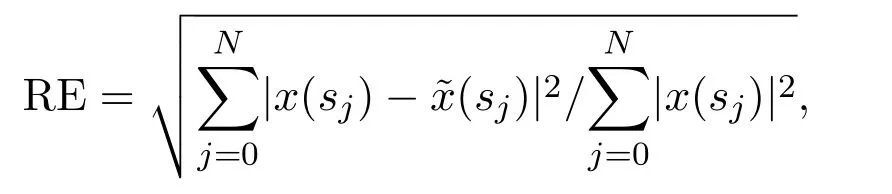
其中,sj为节点,N为区间[a,b]上均匀分布的节点的个数,x(s)为精确解,为数值解.

数值模拟 (12)式,取 [a,b]=[−1,1],H=2,N=100,L=L1,迭代次数选为 15,若正则化参数取为 0时,解的相对误差达到 8.734 983 656 596 983e+006,计算结果严重失真.因此需要正则化处理,本文选取正则化参数为:,初始猜测x(0)=(0.5,0.5,···,0.5),扰动分别为δ=0,0.005,0.01,0.05时,相应的L∞和 RE分别如表1所示,当δ=0,δ=0.05时精确解与数值解的比较如图2和图3所示.迭代次数选为40,δ=0.05时相对误差随迭代次数的变化如图4所示,迭代次数选为15,当δ=0.05时相对误差随迭代次数的变化如图5所示.

表1 同一初始猜测、不同扰动、相同迭代数下所得误差比较

图2 迭代正则化牛顿法所得精确解与数值解的比较,δ=0

图3 迭代正则化牛顿法所得精确解与数值解的比较,δ=0.05

图4 迭相对误差随迭代次数的变化,δ=0.05

图5 迭相对误差随迭代次数的变化,δ=0.05

取迭代次数K=15,扰动δ=0.05时,不同的初始猜测所得误差如表2所示:

表2 不同初始猜测、同一扰动、相同迭代数下所得误差比较

取初始猜测x(0)=(0.5,0.5,···,0.5),扰动δ=0.05时,不同的迭代次数所得误差如表3所示:

表3 相同初始猜测、同一扰动、不同迭代数所得误差比较

从表1可以看出,在初始猜测不变,迭代数相同的情况下,随着扰动的增加,求解误差相对较小,解的稳定性和准确性更高,具体比较见图2和图3.此外,由图4可知,当迭代开始时误差急剧下降,然后趋于平缓,当迭代次数增加时,又出现相对误差变大情况,即半收敛现象,见图5.在实际应用时,可以通过误差限选取迭代次数.从表2可以看出,在扰动水平相同、迭代数相同的情况下,随着初始猜测的变化,相对误差几乎不变,说明在一定的范围内初始猜测对解的影响不大;从表3可以看出,在初始猜测不变、扰动水平相同的情况下,随着迭代数的增加,相对误差有所增加,但精度还是可以接受的.

5 结论

本文采用迭代正则化高斯-牛顿法求解非线性Urysohn积分方程,通过对重力测定中的一个实际问题进行数值模拟,结果表明:迭代正则化高斯-牛顿法在求解此类问题时具有误差小,数值解的稳定性、准确性较高的优点.