The average estimate of the divisor function of integer matrices on square-free numbers

Yang Xiaowei,Lao Huixue

(School of Mathematics and Statistics,Shandong Normal University,Ji′nan 250014,China)

Abstract：Using the classical method in analytic number theory,this paper investigates the mean value of the divisor function of integer matrices on square-free numbers,and establishes an asymptotic formula,which generalized the related result.

Keywords：asymptotic formula,square-free number,divisor function of integer matrix

1 Introduction

LetMk(Z)denote the ring of integer matrices of orderk.We denote the number of different representations of matrixC∈Mk(Z)in the form

References[1-3]studied the distribution of values of the function

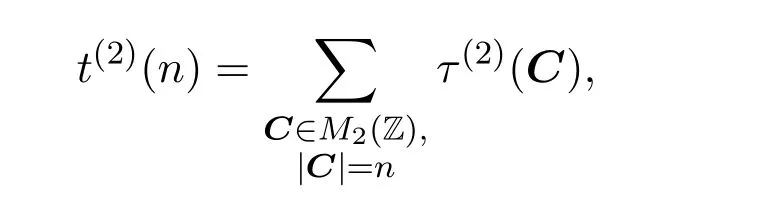
Reference[5]gave bounds for second moment of error term∆2(x)

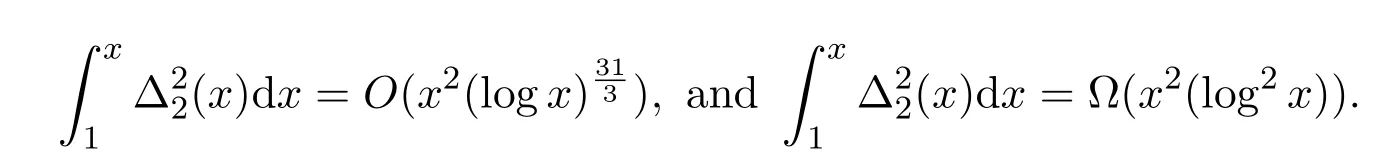
Study of the distribution of functiont(k)(n)fork≥3 has some difficulties.Reference[6]constructed the generating Dirichlet series fort(3)(n)

and obtained the asymptotic formula

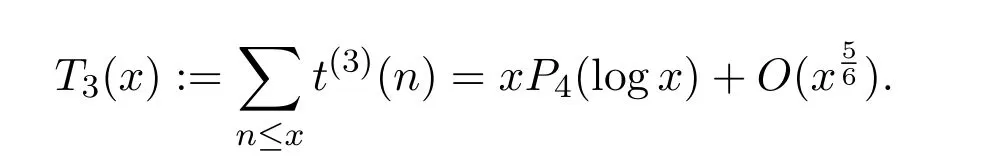
Reference[7]established the asymptotic formula for a summatory function of the number of representations of matrices fromM2(Z)in the formC=A1A2A3,

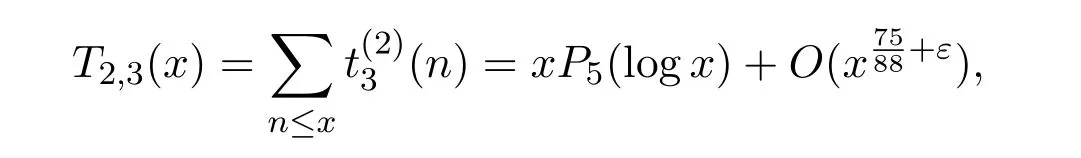
and estimated the error term of this asymptotic formula,where

In this paper,we study the distribution of(n)on the square-free numbers.In detail,we have the following result.

Theorem1.1 Asx→∞,the asymptotic equality

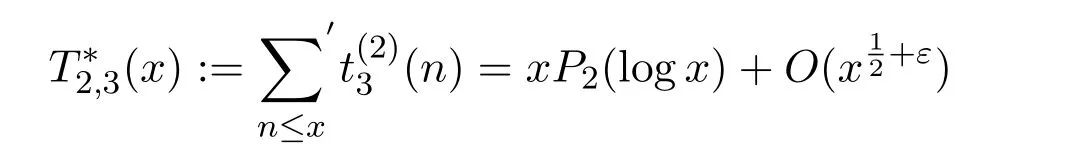
holds,where the sum∑′indicates that the summation runs over square-free numbers.

2 Preliminaries

This section is devoted to give some preliminary results for the proof of Theorem 1.1.

Lemma2.1[7]For each primep>p0,m∈N,

Lemma2.2[5,8-9]For anyε>0,we have

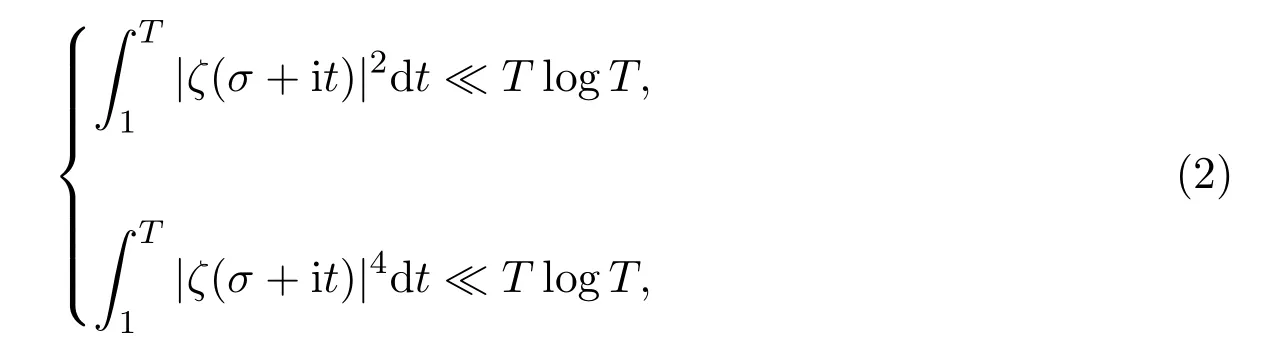
uniformly for|t|>10,T>10 and≤σ≤1+ε,and

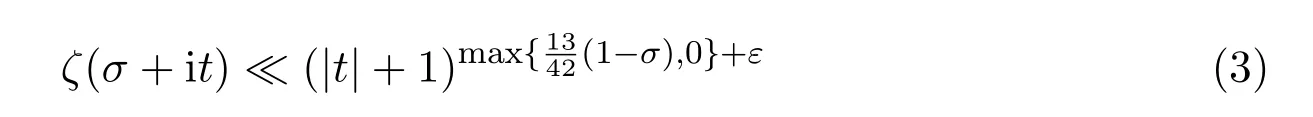
3 Proof of Theorem 1.1

ProofNote that,whereµ(n)is the Mbius function.

First,we will find the Dirichlet generating series corresponding to.By multiplicativity of function(n)and applying Lemma 2.1,we obtain whereG(s)converges absolutely for Res>.

Using Perron′s formula[10],we have

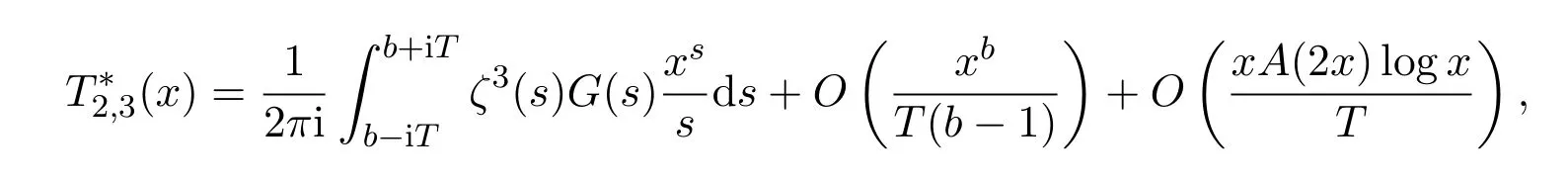
In addition,it is clear that,whereεis an arbitrarily small positive number.

Consider the contour Γ at the points±iT,b±iT.We obtain the following relation

whereP2(u)is the second-degree polynomial with computable coefficients.

Using the estimate of zeta-function(3)in Lemma 2.2,we have

where

and

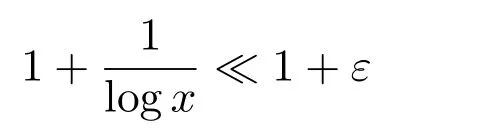
for sufficiently largex.

Thus we can derive the estimate on the horizontal lines

In addition,it is clear that

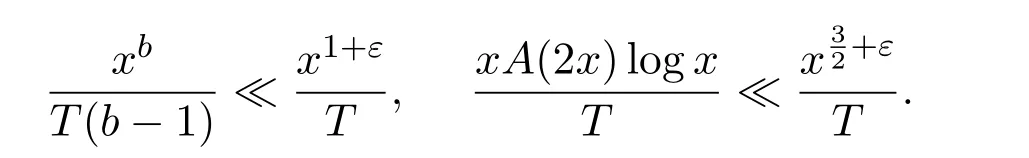
Thus,we have

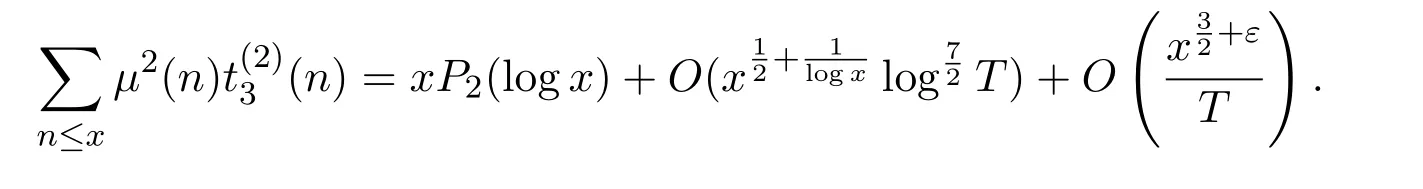
SettingT=x,we obtain the final result

The proof of Theorem 1.1 is complete.