一个具有Filippov控制的植物疾病模型的研究
2019-06-24张田田杨友苹
张田田,杨友苹
(山东师范大学数学与统计学院,山东 济南 250014)
1 引言
植物疾病作为全球重大关注问题之一,不仅在于植物疾病可以造成不可估计的经济损失,严重影响全球经济发展,而且在一定程度上决定了人类的生存,对控制植物疾病至关重要.到目前为止,已有很多数学家运用常微方程模型,脉冲微分方程模型等来研究植物疾病问题[1],提出的措施包括喷洒杀虫剂,释放害虫天敌等,但这些措施实施的同时又会对环境造成一定程度的污染,甚至会破坏一定区域内的生态平衡,因此需要更合理的措施来控制植物疾病的发展.目前已有人提出了可以通过补植无病植株或者移除染病植株等措施来达到控制植物疾病发展的目的[2-5],并建立了具有经济阈值和人文控制策略的植物疾病模型,例如文献[6]提出了一个具有成比例生长率的Filippov植物疾病模型,研究了五种类型平衡点的全局稳定性;文献[7]在此基础上改变了植物的增长方式,考虑了一个常数输入的生长率.然而我们发现考虑一个具有Logistic增长的生长率相对于植物种群更具有现实意义.因此,本文以感染植株作为控制目标,当染病植株数量达到一定的经济阈值时,就采取综合疾病控制策略,即补植无病植株和移除染病植株,否则不采取任何措施.
2 Filippov植物疾病模型
本文建立如下植物疾病模型:

且

其中S(t)和I(t)分别表示易感植株和感染植株在t时刻的数量,a表示易感植株的内禀增长率,表示环境容纳量,β表示感染率,η1和η2分别表示易感植株和感染植株的死亡率,同时假设a>η1,p表示易感植株的补植率,v表示感染植株的移除率.令

则系统(1)和系统(2)可转化为如下模型,


定义2.1 (i)Σ⊂M是滑动段,当且仅当在Σ上有1(Z)>0且

(ii)Σ1⊂M是逃逸区,当且仅当在 Σ1上有,其中表示向量积,n=(0,1)T表示H在M上的梯度.
定义2.2 (i)如果F1(D)=0,H(D)<0,或F2(D)=0,H(D)>0,则称D是真平衡点;
(ii)如果F1(D)=0,H(D)>0,或F2(D)=0,H(D)<0,则称D是假平衡点;
(iii)如果λF1(D)+(1−λ)F2(D)=0,H(D)=0,其中 0<λ<1,
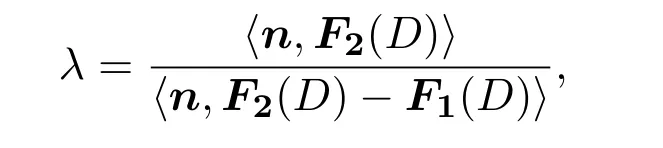
则称D是伪平衡点.
注2.1 由定义可知,只要轨线穿过不连续边界M,系统动力学就会改变,故一个假平衡点不可能稳定.
3 全系统的动力学性态
3.1 子系统 Gi(i=1,2)的动力学性态
子系统G1可以写成如下形式:

由再生矩阵可得 (3)式的基本再生数[8-9]为.明显地,系统 (3)存在一个零平衡点E0=(0,0),无病平衡点和一个地方病平衡点

引理3.1 零平衡点E0=(0,0)是鞍点;如果R1<1,无病平衡点局部渐近稳定;如果R1>1,地方病平衡点局部渐近稳定.
证明系统(3)的雅克比矩阵如下

由a>η1,则 detJ1(E0)=η2(η1−a)<0,故E0是一个鞍点;当R1<1时,

故E10局部渐近稳定;当R1>1时,−tr(J1(E1))>0,det(J1(E1))>0,故E1局部渐近稳定,此时det(J1(E10))<0,则E10是一个鞍点.
引理3.2系统(3)在无极限环.
证明令定义Dulac函数
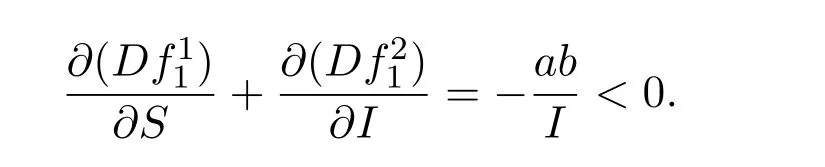
定理3.1 如果R1<1,无病平衡点E10全局渐近稳定;如果R1>1,地方病平衡点E1全局渐近稳定.
证明由引理3.1可知,当R1<1时,无病平衡点E10是局部渐近稳定的;且由引理3.2可知,系统(3)在无极限环,故当R1<1时,无病平衡点E10是全局渐近稳定的.同理,当R1>1时,地方病平衡点E1是全局渐近稳定的.
其次,子系统G2可以写成如下形式:,对于在单连通区域内的轨线,有

子系统G2的基本再生数为:

同样子系统G2存在一个零平衡点E0=(0,0),无病平衡点和一个地方病平衡点
同理于子系统G1的讨论,有如下结论:
定理3.2 如果R2<1,无病平衡点E20全局渐近稳定;如果R2>1,地方病平衡点E2全局渐近稳定.
3.2 全系统的动力学性态
为保证系统(1)正平衡点的存在性,下面只需讨论R1>1及R2>1时全系统的动力学行为.由定义 2.1可知,当且时,即

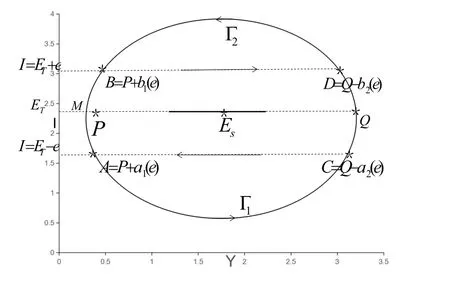
且S1 令g(S(t))=0,得 为保证平衡点的存在性,假设S∗>0,即,则系统 (5)存在唯一的滑动平衡点Es=(S∗,ET),当且仅当S1 从而g(S(t))关于S是单调递减的,故当Es存在时,Es是局部渐近稳定的. 依据阈值ET的取值不同,系统(1)的正平衡点的真假性以及伪平衡点的存在性也不同,通过数值模拟(见图1),做出如下三种情况的猜测: 图1 (a),(b),(c)分别表示系统(1)真平衡点ER1,真平衡点ER2和伪平衡点Es的全局稳定性相图,切平面 M(I=ET),滑动段为 S1S2.η1=0.2,η2=0.4,p=0.6,v=0.6,a=0.3,b=0.2.(a)ET=4.55;(b)ET=7;(c)ET=3. 情况3.1 如果I2 定理3.3 如果I2 证明由引理3.2可知,在子系统G1中无极限环.同理可证,在子系统G2中无极限环.下证在滑动段附近无极限环.令假设 Γ是滑动段附近的极限环 (见图 2),线M(I=ET)上下部分分别为 Γ1,Γ2.令Γ和M的交点为P,Q,Γ和线I=ET+e的交点为 Γ和线I=ET−e的交点为A=P+a1(e),C=Q−a2(e),其中e>0足够小,a1(e),a2(e),b1(e)和b2(e)相对于e都是连续的,且 记Γ1和线段AC围成的区域为D1,Γ2和线段BD围成的区域为D2,由格林公式,有 图2 在情况3.1下,对于系统(1)和系统(2)证明极限环Γ不存在的示意图 这与系统(6)是矛盾的,从而在滑动段附近无极限环.因此,如果I2 情况3.2 如果I2 此时,记真平衡点E1为,假平衡点E2为,伪平衡点Es不存在,因此所有起点在G2中的轨线,无论是否切中滑动段,轨线最终都会进入G1,所有G1中的轨线都会趋于,且是全局渐近稳定的,因此无论轨线的起点是在G1还是G2,它们都将趋于.所以,当给定的经济临界值取值较大时,系统的解最终稳定在子系统G1中,感染植株数量低于经济临界值. 情况3.3 如果ET 记假平衡点E1为,真平衡点E2为,在这种情况下,伪平衡点Es也不存在,则所有起点在G1中的轨线,无论是否切中滑动段,轨线最终都会进入G2,所有G2中的轨线都会趋于,且是全局渐近稳定的,因此无论轨线的起点是在G1还是G2,它们都将趋于.所以,当给定的阈值取值较小时,系统的解最终稳定在子系统G2中,感染植株数量高于经济临界值.事实情况下,选择一个相对较小的经济临界值是不合理的,否则将会造成重大的经济损失. 本文研究了一个具有Logistic增长的植物疾病Filippov模型的动力学性质,得到了系统的基本再生数以及平衡点的存在性和稳定性,并通过数值模拟预测了系统的全局稳定性.结果表明,基于阈值的取值,系统的解最终稳定在子系统的真平衡点或者滑动系统的伪平衡点.
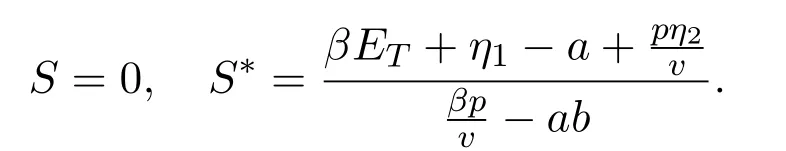
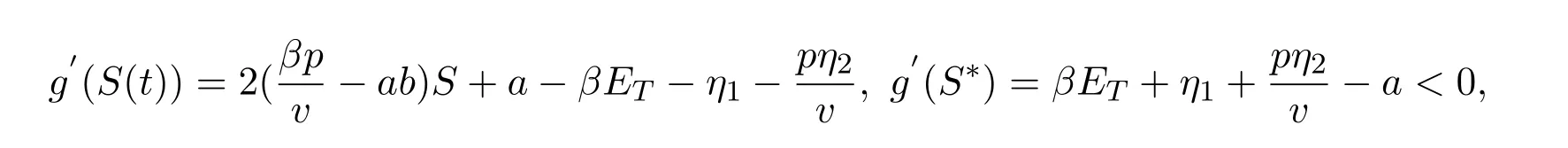

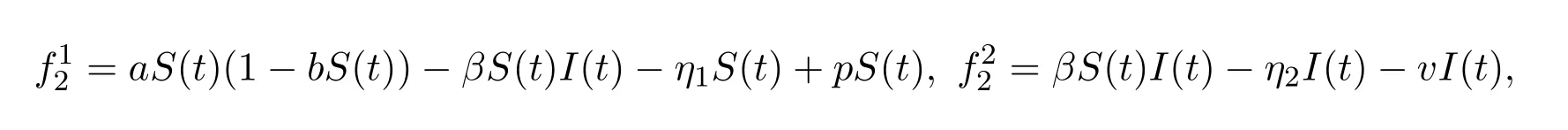

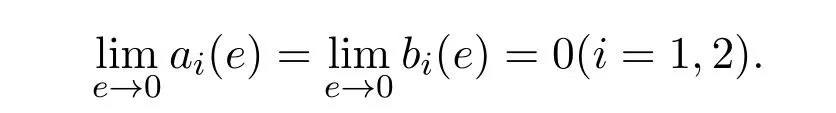
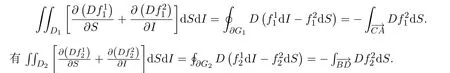

4 结论
