变电站混凝土构架梁的损伤识别

于周平 杨伟军

(1.绍兴文理学院 元培学院，浙江 绍兴 312000； 2.长沙理工大学 土木工程学院，湖南 长沙 410076)

0 引言

20世纪八九十年代，我国早期建设的变电站构架多为钢筋混凝土结构.在其使用过程中，由于疲劳荷载、环境腐蚀、材料老化、构件缺陷等因素的作用，结构逐渐产生损伤累积[1-2]，从而使其承载能力降低，抵抗自然灾害能力下降，影响结构的安全使用.其中，绝缘子吊环、避雷针与构架连接处损伤将直接引发高压线掉落等重大电力安全事故.因此，及时发现损伤与修补损伤，对于延长结构的使用寿命至关重要.变电站检测常用的方法是对结构进行全面的检查和加固，尤其是变电站构架的上部结构必须在停电条件下利用观测法进行检测.但观测结果不够准确，且存在漏检的情况，可操作性不强.因此，采取合适的方法对变电站构架结构进行检测非常重要.无损检测技术不仅可准确可靠地判断损伤的程度、位置，还可为变电站构架结构的加固与维修提供依据，保证构架结构安全使用.由于变电站构架梁的特殊性，根据动力学损伤诊断方法和原理，通过环境激励的方法获取结构的模态和频率识别构架梁的损伤情况，从而实现健康监测的目标.结构的模态对局部损伤不太敏感，识别效果较差.而固有频率具有测量简单、精度高的特点[3-5].国内外学者研究出很多利用固有频率对结构进行损伤识别的方法[6-9]，使基于频率的损伤识别效果大大改善.因此，基于频率的损伤识别法对于变电站构架结构的损伤识别是非常理想的方法.本文主要讨论正则化频率变化率和多裂缝损伤识别法在变电站构架梁损伤识别中的应用，证明了该方法对变电站构架梁进行损伤识别的有效性 .

1 正则化频率变化率法

1.1 正则化频率变化率法的基本理论

正则化频率变化率是指损伤前后的频率变化率，与损伤程度和位置有关[10-12]，即：

(1)

其中r为损伤位置的向量.将fi在fi(0,0)处忽略高阶项,按二级数展开可得：

(2)

假定结构无扰动，取fi(0,0)=0，上式简化为：

(3)

函数fi在ΔK=0和ΔM=0处的偏微分为常数.上式简化为：

FFCi=ΔMmi(r)+ΔKni(r).

(4)

结构的损伤主要表现为刚度和质量的变化[13]，但质量的变化很小，假定ΔM=0，则

FFCi=ΔKni(r).

(5)

因此，正则化的频率变化率为[14-15]：

(6)

其中式(6)为第i阶正则化频率变化率，q为频率的阶数.

1.2 混凝土构架梁的损伤指纹库

1.2.1 混凝土构架梁的损伤模型

本文以某变电站的混凝土构架梁为例进行损伤分析.该构架梁的两侧都有挂线，为简化结构，将挂线平面外偏角设为0°，根据挂线的长度计算挂线的水平荷载为4 kN.构架梁的截面及尺寸见图1.

利用ANSYS软件计算构架梁在不同损伤位置的固有频率，建立频率指纹库.在该模型中将构架梁的全长划分为20个单元，通过改变单元的弹性模量模拟损伤.

图1 构架梁简图及详图注：构架梁只有两端和中点位置为1-1断面，其他位置为2-2断面

本模型只考虑单一位置的损伤，且单元的宽度为构架梁的损伤宽度.

构架梁的刚度为弹性模量与截面惯性矩的乘积.不考虑损伤给单元带来的截面惯性矩的变化，则构架梁的刚度只与弹性模量有关.令单元的弹性模量为Ed=(1-α)E,其中α为损伤因子，E为构架梁无损伤时的弹性模量.构架梁为钢筋混凝土结构，该梁的弹性模量由钢筋和混凝土两部分组成.但是钢筋面积在梁截面面积中的占比较小，因此，在建模过程中忽略钢筋弹性模量的变化.

1.2.2 混凝土构架梁损伤定位指纹库的建立

由文献[16]得知，动力指纹随着结构损伤程度的增加而变化不大.因此本文只研究损伤位置对动力指纹的影响.由于模型构架梁呈对称结构，因此只需要分析半结构的损伤情况.为了得到比较明显的频率指纹，令损伤因子为0.6，即Ed=0.4E分别在无损伤状态下及在具有一个损伤因子为0.6的损伤单元下，利用有限元分析计算出模型构架梁在不同的损伤位置状态下的前3阶固有频率f1、f2、f3，详见表1.表1中的损伤相对位置是指损伤单元的中心位置x与梁长L的比值；构架模型梁的各阶正则化的频率变化率NRFi是由ANSYS计算的频率值，按照式(6)计算而来.

如图2所示，对称结构的正则化频率变化率曲线均呈对称分布.因此，单一的动力指纹无法准确识别对称结构的损伤.低阶的正则化频率变化率曲线在某一区域呈单调变化.图2中当x/L为0.25～0.375时，NRF1与损伤位置的曲线呈现为单调变化，NRF1与损伤位置一一对应.图3中当x/L为0.35～0.50时，NRF2与损伤位置的曲线也呈现为单调变化.

从图2～图4中可以看出,在损伤单元位置移动的范围内，NRF3曲线重复两次，NRF2重复一次，而NRF1曲线无重复.因此可以得知，高阶的正则化频率变化率曲线重复性多，单调性差；低阶的正则化频率变化率曲线单调性好，损伤识别更准确，误判概率低.

表1 模型梁在不同位置损伤时的频率及其动力指纹

损伤的相对位置f1/Hzf2/Hzf3/HzNRF1NRF2NRF3无损伤50.508200.270448.770 — — —0.02550.407199.472447.9720.261 50.512 10.226 40.05050.386199.036446.6610.185 10.464 10.350 70.07550.347198.592445.5010.172 20.444 80.383 10.10050.309198.274444.4130.169 90.422 40.407 80.12550.283197.860443.3260.158 60.421 00.420 40.15050.228197.375442.0410.161 40.413 60.425 00.17550.187196.600440.8170.152 70.432 70.414 60.20050.099195.733439.5700.160 90.442 40.396 60.22550.052195.621440.9160.184 70.466 70.348 60.25049.962195.326442.1170.218 30.490 10.291 60.27549.915195.449442.4590.239 10.481 90.278 90.30049.826195.985443.7360.297 10.462 60.240 30.32549.783196.885445.2750.372 40.430 90.196 70.35049.698197.301446.9730.464 70.422 20.113 00.37549.701197.866447.8190.535 50.395 40.069 20.40049.610197.385445.6040.517 00.364 80.177 00.42549.585197.788445.2270.479 10.319 30.201 50.45049.580198.018442.6800.430 90.259 20.309 90.47549.430197.673440.9160.417 40.249 30.333 30.50049.245197.895438.5770.425 40.198 30.376 3

x/L图2 第一阶正则化频率变化率曲线

x/L图3 第二阶正则化频率变化率曲线

从图5～图7中可以看出,依据正则化频率变化率的组合曲线单调性特点，损伤位置的识别更准确.NRF1与NRF2的组合曲线，可发挥各自单调性的优势，损伤位置的识别效果较好.而NRF3与其他曲线组合的识别效果较差，NRF3在曲线组合作用不大.所以，低阶的正则化频率变化率的组合曲线损伤位置识别效果好，而高阶的正则化频率变化率单调性差，在曲线组合中的意义不大.

2 多裂缝损伤识别法

2.1 多裂缝损伤识别法基本原理

不考虑结构阻尼的基本运动方程为：

x/L图4 第三阶正则化频率变化率曲线

x/L图6 NRF1和NRF3的组合曲线

(K-ω2M)Φ=0.

(7)

考虑损伤引起各参数的变化，利用摄动法求解方程可得：

[(k+ΔK)-(ω2+Δω2)(M+ΔM)](Φ+ΔΦ)=0.

(8)

结构的损伤主要表现为刚度和质量的变化，但质量的变化很小，假定ΔM=0，将方程展开并忽略其二项式得：

(9)

(10)

令单元损伤系数矩阵[ΔKN]=αN[KN]，则矩阵的元素为：

(11)

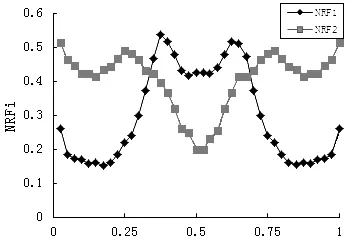
x/L图5 NRF1和NRF2的组合曲线

x/L图7 NRF2和NRF3的组合曲线

(12)

Si，N为刚度变化的特征值敏感度系数，N为总单元数.将式(12)表示成矩阵形式：

[Z]=[S]α，

(13)

(14)

模态应变能的变化与固有频率的变化关系[18]为：

(15)

其中Wi和ΔWi分别为结构在无损伤状态下的第i阶模态应变能和损伤后的应变能的变化量.研究不考虑扭转变形，Euler-Bernoulli梁的任意阶模态应变能Wi为[19]：

(x)}2dx.

(16)

其中E、I和L分别为弹性常数模量、惯性矩以及梁的跨度；Φi(x)为第i阶振型函数.

根据线弹性断裂力学的基本理论可得到模态应变能的损失率为：

(17)

其中μ为泊松比，b为梁的截面宽度.Ki是与弯曲应力σ、裂缝深度a及梁的维数等因素有关的应力强度因子，即：

(18)

γ为与裂缝相对高度有关的几何因子[19].小裂缝时，取γ=1.12.

(19)

aN=a(xN)表示沿梁轴线方向在位置xN处的裂缝大小；σN=σ(xN)为沿梁轴线方向在位置xN处的最大弯曲应力.根据Euler-Bernoulli梁的应力表达式为：

(xN)，

(20)

(21)

联立式(11)、(14)和(20)求解得：

(22)

其中

ζ=3π(1-μ2)γ2h.

(23)

假设将梁划分成m等份，测量其前q阶频率.将式(21)表示成矩阵形式[20]：

[Z]qxi=[S]qxm{D}mxi，

(24)

其中简支梁的

(25)

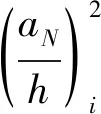
2.2 混凝土构架梁的多裂缝损伤识别

2.2.1 混凝土构架梁的模型及其敏感度矩阵

在上节中，降低模型梁的刚度使固有频率变化不大明显.本节采用分离式建模，通过删除单元的方式模拟结构损伤，通过块体循环的方式建立混凝土模型,模型的其他参数与上节相同.

由式(24)可知，识别的精度与划分的单元数有关，单元数越多，识别精度越高，但计算量也越大.根据构架梁的情况，结合计算精度的要求，将模型梁划分为10个单元.根据式(25)，其敏感度矩阵S计算结果如式(26)所示.

2.2.2 多裂缝识别法的损伤定位

在本构架梁模型中，在1/10L和2/5L即第一单元和第四单元处设置单一裂缝,以防止节点的影响.此外，为了验证多裂缝识别法在多裂缝情况下识别的有效性，设计了四种情况进行分析,即：多裂缝情况1——在第三单元、第四单元设计裂缝，其裂缝的相对高度分别为0.50和0.10；多裂缝情况2——在第一单元、第四单元设计裂缝，其裂缝的相对高度分别为0.20和0.30；多裂缝情况3——在第五单元、第三单元设计裂缝，其裂缝的相对高度均为0.50；多裂缝情况4——在第四单元、第三单元及第九单元设计裂缝，其裂缝的相对高度均分别为0.60、0.30和0.50.利用ANSYS计算构架模型梁在各种损伤状态下的前10阶频率值，结果见表2.根据计算出的频率和敏感度矩阵，利用MATLAB求解式(24)得出损伤因子D，具体结果见表3.

表2 构架梁在各种损伤状态下的前10阶频率值

损伤位置a/hf1/Hzf2/Hzf3/Hzf4/Hzf5/Hz无损伤—50.508200.270448.770764.3101 177.2950.0550.465200.089448.628763.9281 176.4700.1050.382199.799448.006761.9531 174.879第一单元0.2050.249199.246446.971759.9801 172.5170.3049.722199.045445.708760.0951 168.3130.5049.361196.785445.097756.0101 158.3050.0550.293199.608447.264760.5171 173.6400.1050.207198.894446.927758.6341 170.9800.2049.931196.346445.640746.9941 162.783第四单元0.3049.392 196.376444.123747.2281 156.4490.5048.391194.324443.012733.6981 139.7890.6048.052189.443435.399722.6681 118.9880.7547.553189.040435.423689.7451 103.145多裂缝情况1—47.203173.589378.220756.8221 077.723多裂缝情况2—49.596194.272446.272737.5891 154.590多裂缝情况3—46.624145.716372.073709.3691 013.842多裂缝情况4—46.327158.782388.956746.1331 016.435

续表2

损伤位置a/hf6/Hzf7/Hzf8/Hzf9/Hzf10/Hz无损伤—1 700.1722 296.4982 975.4154 204.8124 400.5910.051 698.8112 294.5452 973.4814 202.0784 594.6520.101 697.7902 291.4412 969.6074 196.3944 588.437第一单元0.201 695.0632 287.0632 964.3864 188.1704 579.2120.301 684.8862 278.2842 952.5664 176.3334 562.7940.501 666.7752 251.6232 929.2364 137.4164 523.7080.051 697.0242 289.5992 966.6254 192.1794 583.5970.101 693.4422 283.0242 961.3984 182.0454 573.2070.201 690.8802 262.9542 948.0654 152.3454 541.199第四单元0.301 675.3382 248.5752 935.1234 132.0714 516.4580.501 655.1152 204.2802 899.7714 075.2194 451.1580.601 621.5042 162.9792 860.2703 991.4724 370.1560.751 631.0132 118.2632 818.4903 928.0694 308.037多裂缝情况1—1 465.5052 169.9172 780.2223 834.4574 208.999多裂缝情况2—1 684.8862 238.4672 935.2744 123.0754 508.963多裂缝情况3—1 383.0042 008.3532 625.6253 557.2313 959.513多裂缝情况4—1 324.4981 979.3892 666.6093 626.3923 969.644

表3 构架梁在各种损伤状态下的损伤因子

损伤位置a/hD1D2D3D4D50.05-0.060 5-0.002 7-0.004 4-0.005 3-0.005 70.10-0.062 7-0.002 6-0.003 4-0.003 8-0.004 0第一单元0.20 0.065 0-0.000 6-0.000 6-0.000 6-0.000 50.30 0.165 4-0.003 3-0.000 1-0.001 8-0.002 90.50 0.682 4-0.306 1-0.011 9-0.414 7-0.016 40.05-0.063 6-0.002 8-0.002 7 0.000 7-0.002 60.10-0.067 7-0.000 2-0.000 5 0.001 8-0.001 00.20-0.079 1-0.003 3-0.007 6 0.113 7-0.011 1第四单元0.30-0.087 1-0.001 4-0.009 6 0.322 6-0.016 20.50-0.112 1-0.007 3-0.012 7 1.216 1-0.028 60.60-0.150 8-0.028 5-0.047 5 2.056 9-0.062 60.75-0.189 3-0.009 6-0.029 9 3.249 7-0.061 5多裂缝情况1—-0.179 8-0.273 2 1.416 3-0.235 3-0.204 8多裂缝情况2—-0.091 9-0.002 4-0.011 5 0.816 0-0.018 7多裂缝情况3—-0.276 8-0.381 8 1.671 0-0.160 1 1.897 3多裂缝情况4—-0.313 9-0.351 2 1.644 0 0.294 3-0.282 9

续表3

损伤位置a/hD6D7D8D9D100.05-0.006 1-0.008 3-0.007 4-0.004 7-0.004 90.10-0.004 1-0.009 4-0.005 1-0.006 2-0.001 8第一单元0.20-0.000 6-0.011 3-0.000 5-0.008 6-0.002 70.30-0.003 5-0.018 1-0.010 6-0.015 6-0.012 40.50-0.017 5-0.024 5-0.031 6-0.024 3-0.032 30.05-0.002 6-0.010 6-0.003 2-0.007 7-0.000 50.10-0.001 2-0.011 7-0.002 0-0.009 5-0.005 80.20-0.011 0-0.011 9-0.014 7-0.012 8-0.023 7第四单元0.30-0.017 8-0.020 5-0.028 8-0.021 7-0.036 50.50-0.032 6-0.031 1-0.057 0-0.035 8-0.072 70.60-0.066 4-0.044 9-0.094 3-0.053 9-0.103 80.75-0.069 4-0.049 1-0.097 4-0.062 4-0.136 3多裂缝情况1—-0.197 2-0.118 3-0.220 5-0.127 2-0.119 2多裂缝情况2—-0.020 5-0.012 1-0.628 7 0.416 3 -0.043 2多裂缝情况3—-0.300 5-1.131 7-0.335 1-0.160 1-1.211 5多裂缝情况4— 2.875 1-0.138 9-0.337 8 1.316 0-0.224 9

表4 损伤识别结果

损伤基本情况识别结果损伤位置裂缝相对高度a/h损伤位置裂缝相对高度a/h第一单元0.05无损伤—第一单元0.10无损伤—第一单元0.20第一单元0.093第一单元0.30第一单元0.149第一单元0.50第一单元0.303第四单元0.05第二单元0.009第四单元0.10第四单元0.015第四单元0.20第四单元0.124第四单元0.30第四单元0.208第四单元0.50第四单元0.405第四单元0.60第四单元0.527第四单元0.75第四单元0.662第三单元0.50第三单元0.437第四单元0.10第一单元0.20第四单元0.332第四单元0.30第五单元0.50第五单元0.506第三单元0.50第三单元0.475第三单元0.30第三单元0.471第四单元0.60第四单元0.623第九单元0.50第九单元0.421

表4为损伤识别结果.由表4可知，基于频率的多裂缝识别法能够识别单一损伤和多处损伤的情况.该方法对裂缝位置的识别精度取决于构架模型梁划分的单元数(段数)，划分的单元数越多，识别精度越高.但对裂缝深度的识别还欠准确.

多裂缝识别法对轻度损伤识别的效果不理想，尤其是在支座附近.该方法能够较好地识别中度损伤的位置和损伤程度；但对于损伤严重的情况，能准确地识别损伤位置，但损伤程度的识别有误差.若分析单元中有多处裂缝，则对裂缝高度较大的中度损伤的识别较为准确.

多裂缝识别方法中矩阵方程的求解对频率的改变量很敏感.敏感度矩阵计算精度会影响损伤因子的准确度.

3 小结

我国早期建设的变电站结构持续使用到现在损伤在所难免.变电站构架的上部结构以往只能在全面停电的情况下采用观测法检测.这种方式代价大，观测结果不准确.固有频率易测、精度高，在无损检测中效果较好.通过利用正则化频率变化率法和多裂缝识别法对变电站构架梁损伤的分析，得到如下结论：

(1)正则化频率变化率法可以识别构架梁的单一损伤，多裂缝识别法能够识别单一损伤和多处损伤的情况.

(2)对称结构的正则化频率变化率曲线均呈对称分布，单一的动力指纹无法准确识别对称结构损伤.高阶的正则化频率变化率曲线重复性多，单调性差，识别效果差.低阶的正则化频率变化率曲线单调性好，损伤识别更准确，误判率低.正则化频率变化率的组合曲线能够发挥各曲线的单调性特点，损伤位置的识别更准确.

(3)多裂缝识别法对损伤位置识别的精度取决于构架模型梁划分的单元数，划分的单元数越多，识别精度越高.该方法对轻度损伤的识别效果不理想，但能够较好地识别中度损伤的位置和损伤程度.对于损伤严重的情况，能准确地识别损伤位置，但损伤程度的识别有误差.