数学分析中几种常见的不等式证明方法

杨 涛

（四川工商学院数理教研室，四川 成都 611745）

1 引言

不等式的证明是高等数学中重点和难点之一，其常用证明方法有：比较法、综合法和数学归纳法、利用导数的定义、函数的单调性、最值性(极值性)和中值定理等［1，2，3，4，5］。然而许多学生在证明不等式时总是感到束手无策、无从下手。一方面是因为不等式证明的题目类型比较多，证明方法因问题的不同而变化多端；另一方面是在学习的过程中对不等式证明方法没有进行归纳和总结。因此，为帮助学生较好理解和掌握不等式证明问题、熟练运用所学知识证明不等式，下面对不等式证明常见方法进行了归纳和总结，帮助学生较好地理解和掌握不等式证明问题。

1.1 借助函数图形分析不等式

函数图形不但能够清晰直观地呈现函数增减变化、对称性、最值等问题，而且是分析不等式成立的最基本和最常见的方法之一。比如，要证明f（x）＞g（x)，可借助计算机分别画出函数f（x）与g（x)的函数图形，对画出的函数图形进行分析和探讨，得出不等式成立的相关信息，并根据得到的不等式成立相关信息梳理不等式证明思路，同时以相对简洁且符合逻辑的数学语言对待证不等式进行描述。

例1 证明：当x＞0 时，x＞ln（1+x）.

分析1 不妨记f（x）=x，g（x)=ln（1+x），要证明，x＞ln（1+x）在x＞0 时成立，即f（x）＞g（x)证明。函数图形能够清晰直观地帮助我们证明不等式问题，因此函数f（x）与g（x)的函数图形如图1所示。图1表明，当x＞0 时，恒有f（x）＞g（x），即x＞ln（1+x）。

分析2 要证明x＞ln（1+x）在x＞0 时成立，即证明ex＞1+x。不妨记f（x）=ex，g（x）=1+x，函数f（x）与g（x）的函数图形如图2所示。图2表明，当x＞0 时，恒有f（x）＞g（x），即ex＞1+x，等式左右两边同时取对数可得：当x＞0 时，不等式x＞ln（1+x）成立。

图1 函数f（x）=x 与g（x)=ln（1+x）图像

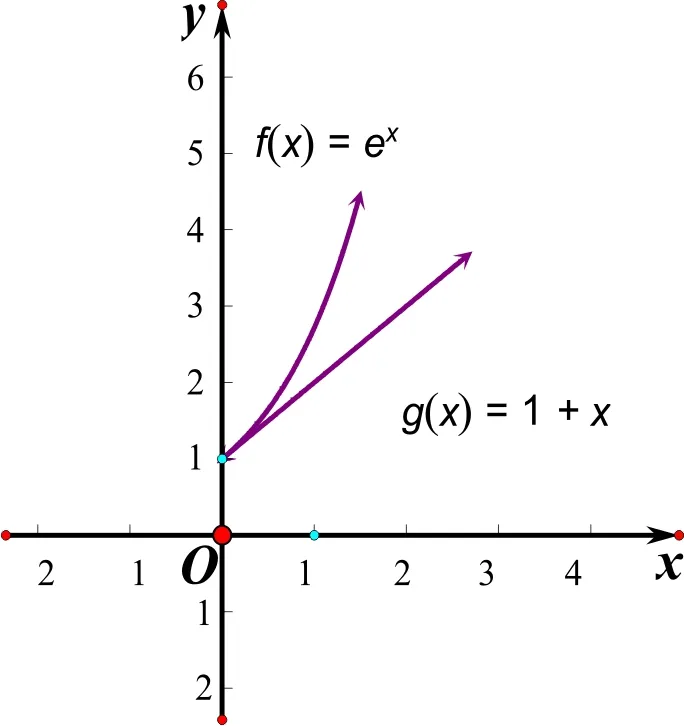
图2 函数f（x）=ex 与g（x）=1+x 图像

上述分析1、分析2 表明，当x＞0 时，不等式x＞ln（1+x）恒成立，亦即解析式f（x）=x-ln（1+x）在x＞0时严格单调递增。因此，实例1 可利用单调性证明。

1.2 利用单调性证明不等式

函数单调性的判定不但是求最值、研究函数在定义域内变化形态的有效方法，而且也是证明不等式成立的基本方法，其利用单调性证明不等式要点如下：若f ′（x）≥0（或f ′（x）＞0），则x1＜x2时，有f（x1）≤f（x2） （或f（x1）＜f（x2））。实例1 利用单调性证明方法如下：

证 记f（x）=x-ln（1+x），知D（f）=｛x|x＞-1｝。由题意可知x＞0，于是f（x）的定义域D（f）=｛x|x＞0｝。

因对任意x，x+Δx∈D（f）且Δx→0 时，有

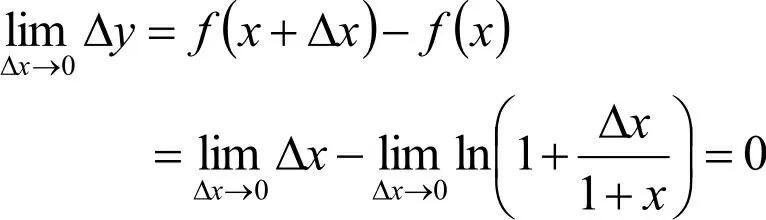
所以函数f（x）在其定义域D（f）内连续。又因极限存在，即函数f（x）在其定义域D（f）内可导。

图3 函数f（x）=x-ln（1+x）图像

上述方法首先利用定义证明了函数f（x）在其定义域内连续可导，根据函数f ′（x）恒大于0，即函数f（x）在其定义域内严格单调递增。若不等式f（x）的最小值min f（x）≥0（x＞0），则x＞ln（1+x）。

1.3 利用求极值的方法证明不等式

极值方法证明不等式要点： 若需证明f （x）≥g（x)不等式成立，则证明的最小值都大于零。利用求极值方法证明实例1 过程如下：

证 记f（x）=x-ln（1+x）（当x＞0 时）。因F（0）=0，所以只要证明

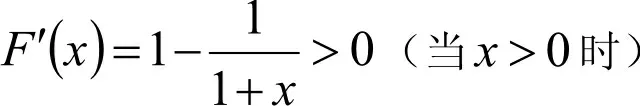
因f（x）在D（f）=｛x|x＞0｝内连续可导，即实例1也符合拉格朗日中值定理条件，因此该例也可运用拉格朗日中值定理证明。

1.4 利用拉格朗日中值定理证明不等式

本节利用文献［1］回顾拉格朗日中值定理有关概念。若函数f（x）满足：(1)在闭区间[a，b]上连续；(2)在开区间（a，b）内可导，则至少存在一点ε∈（a，b）内，使得

成立。在了解和掌握拉格朗日中值定理相关概念后，可知上述实例（例1）满足拉格朗日中值定理条件，即运用拉格朗日中值定理证明实例1 过程如下：

证 令f（x）=x-ln（1+x），因为f（x）在[0,+∞]上连续可导.即

则f（x）在区间[0，x]上满足拉格朗日中值定理条件，所以在区间[0，x]中至少存在一点ε（ε∈[0，x]），使得f（x）-f（0）=f ′（ε）（x-0），而

由于ε＞0，知f ′（ε）＞0.又f（0），故当x＞0 时，f（x）=xf ′（ε）＞0，于是，有x-ln（1+x）＞0，即x＞ln（1+x）。

因f（x）在D（f）=｛x|x＞0｝内n 阶连续可导，即实例1 也可用Taylor 公式证明，其证明方法如下：

1.5 利用泰勒（Taylor）公式证明不等式

为能较好的理解、 掌握和应用Taylor 公式证明不等式，本小节利用参考文献［1］对Taylor 公式基本要点做简要回顾。若f（x）在[a，b]上有连续n 阶导数，且满足

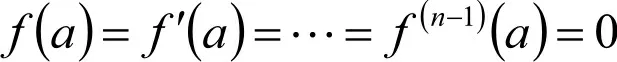
f（n）（x）＞0（当x∈（a，b 时），则

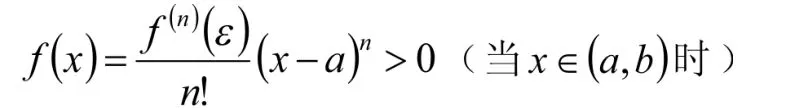
利用此原理，可证例1。

证 原式等价于f（x）≡x-ln（1+x）＞0，因f（0）=f ′（0）=0。

1.2～1.5 节对同一问题不同证明方法进行了粗略的归纳和总结，学生若在学习过程中能较好理解和掌握上述不等式证明理论基础，并熟练运用到不等式证明中，不但能培养学生不等式证明的发散思维，而且也为今后提出新颖的不等式证明方法打下夯实的基础。下面介绍几种积分不等式的证明方法。

积分不等式是指两个以上的定积分不等式。关于积分不等式，这里仅介绍微分学方法证明不等式和不等式两端取变限积分证明不等式的证明方法。

1.6 利用微分学的方法证明不等式

在介绍微分学方法证明不等式前，首先需掌握和理解不定积分与求导数或微分互为逆运算的相关性质：（1）

例2 设f（x）在[0，1]上可微，且当x∈（0，1）时，0＜f′（x）＜1，f （0）=0，试证：

证 方法一：问题在于证

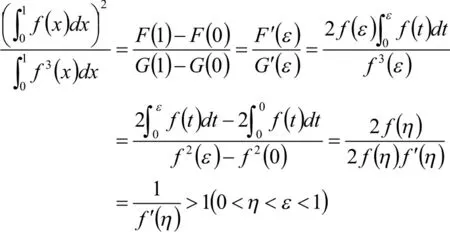
已知f（0）=0，0＜f ′（x）＜1（当x∈（0，1）），故x∈（0，1）时f （x）＞0。下证（1）式大于0.记则r（0）=0，

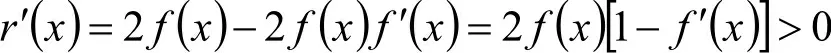
1.7 不等式两端取变限积分证明新的不等式

不等式两端取变限积分证明不等式时，首先需掌握积分基本公式：

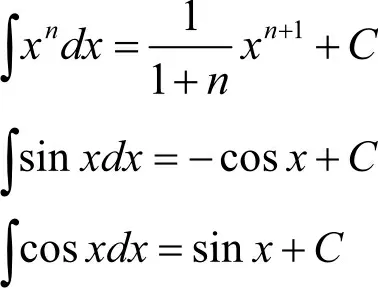
证 已知x＞0 时，cos x≤1，（当x=2nπ 时等号成立）。对不等式cos x＜1 两端同时取[0，x]上的积分，得

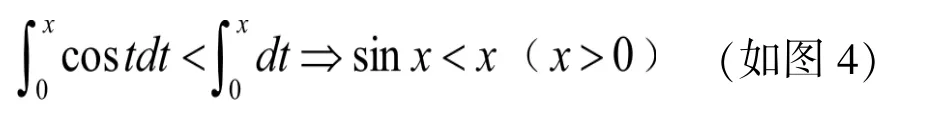
再次对不等式sin x＜1 取[0，x]上的积分，得

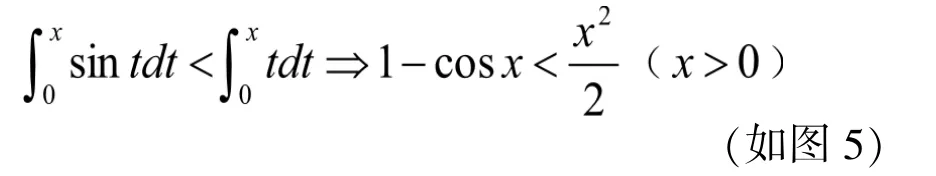
即

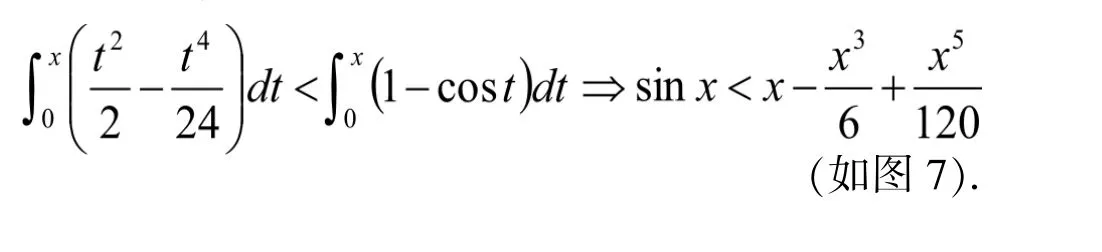
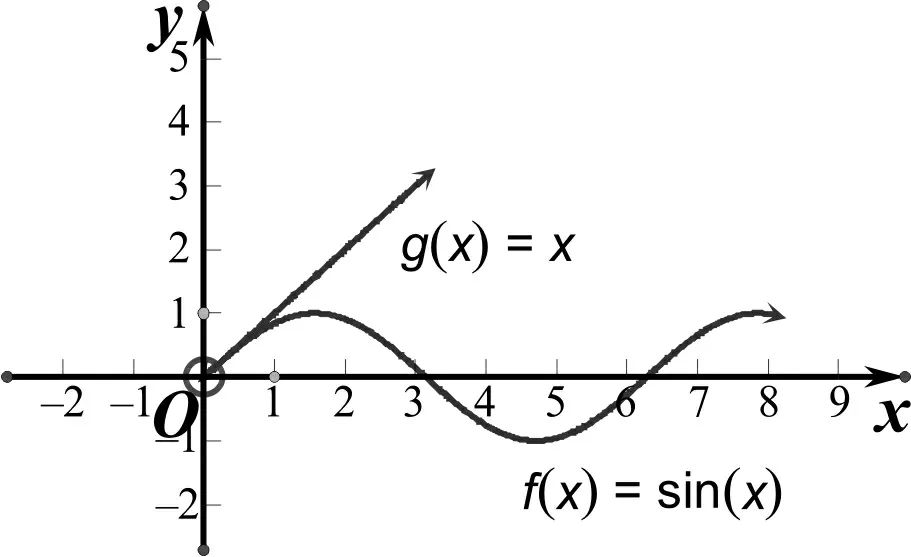
图4 函数f（x）=sin x 与g（x）=x图像

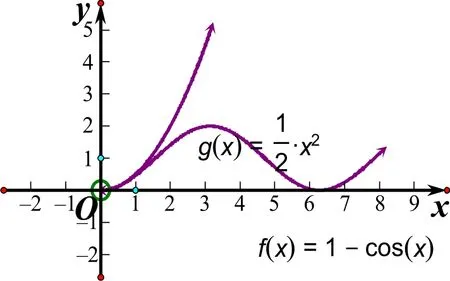
图5 函数f（x）=1-cos x 与

图6 函数f（x）=1-cos x 与图像

图7 函数、g（x）=sin x 与图像

上述过程介绍了通过对不等式两端同时取积分的方式证明不等式，并给出了积分后新的不等式的函数图形，进一步验证证明过程的正确性。

2 结束语

以上讨论了不等式证明的几种方法，但是不等式证明问题是多种多样、错综复杂的，不是几种类型的不等式证明方法所能概括的，但只有熟练的掌握一些最基本、最常用的不等式证明方法，才能帮助我们能够更好的解决不等式证明问题，才能从这些最基本、最常用的不等式证明方法中获得启发，进而给出新颖的不等式证明方法。从文中介绍的不等式证明方法中可以看到，熟练的掌握函数单调性、极值求解方法、微分、中值定理、Taylor 公式等是有效的解决不同形式的不等式证明问题基本方法和手段，也是有效的启发自己对不等式证明思维训练、不等式应用背景理解和对不等式证明方法的进行一步的延拓的基础。