基于连续均方误差准则的EMD 去噪算法在高光谱数据中的应用

武 进

（四川工商学院云计算与智能信息处理重点实验室，四川 成都 611745)

1 前言

在客观条件下采集的光谱数据会含有噪声，因此需要在数据分析之前对数据采取滤波处理。而由于高光谱数据的特性，一般实用方法如小波变换等滤波法都存在着一定的不足之处。EMD 算法本质上是以时间特征尺度为度量，以信号为极值的时空滤波器，能够清晰地反映数据信号的波动和趋势，所以在理论上可以将EMD 应用于信号数据去噪［4，9］。

2003年，Huang 等人对白噪声进行EMD 分解试验，研究了白噪声的IMF 特性，认为其能量密度和平均周期是一个常数，该研究成果为以后人们将EMD 应用于信号去噪领域打下了基础。法国学者Flandrin 将EMD 看作是类似小波分解的二进滤波器组，并建立了信号被白噪声污染时的去噪方法。Rilling 将EMD 方法应用于研究分形高斯噪声的赫斯特指数与分解分量序数之间旳关系，认为可以根据分解分量序数估计出分形高斯噪声的赫斯特指数［2，8］。

经EMD 分解后，原始信号的局部特征在各分量中都得到了反映，从相关文献中可知信号噪声主要处于高频部分，而能量主要处于低频，由此可以通过将高频和低频进行分离从而达到对噪声和能量进行区分的目的。据此原理，考虑高光谱数据的光谱特征，本文运用EMD 分解对高光谱数据进行去噪处理。

2 EMD 简介

经验模态分解（Empirical Mode Decomposition，EMD）法是黄锷（N.E.Huang）于1998年提出的一种新型自适应信号时频处理方法，特别适用于非线性非平稳信号的分析处理。

EMD 方法与傅里叶变换、小波变换的核心思想一致：将信号分解为各个相互独立的成分的叠加，不同点在于EMD 进行信号分解是根据信号本身的时间尺度特征，具备自适应性，而傅里叶变换和小波变换都需选择合适的基函数，因此EMD 分解适用范围更广。

EMD 分解是将信号分解为多个本征模函数（IMF）的叠加。IMF 必需要满足下面两点：

（1）函数在整个时间范围内，局部极值点和过零点的数目必须相等，或最多相差一个；

（2）在任意时刻点，局部最大值的包络（上包络线） 和局部最小值的包络（下包络线） 平均必须为零。

3 经验模态分解在滤波中的应用

3.1 EMD 滤波特性

经验模态分解过程实质上是基于自适应二进滤波器组的一种滤波。因此具有基于其自适应滤波的性质创设新型的自适应滤波器的可行性。在实际应用中，可以依所选原始数据的性质，舍弃对应的特征模态函数，由剩余的进行重构［5，7］。

根据上述原理，如果简简单单的对原始数据进行舍弃，很有可能滤除有用成分；再者，其施行EMD分解由于信号本身的特征差异，从而也导致所得的IMF 分量数量也不同；最后，因为噪声类型的不同，所以其具体分布也不一致。综上，采取EMD 分解原理进行数据去噪处理由于结果的误差较大因此在此原理的基础上还需进行改进。

3.2 连续均方误差准则

为了对上述原理进行改进，即判断选取的IMF个数，文章采用了连续均方误差的方法。该方法通过计算两个相邻特征模态函数间的均方误差，从而达到判断舍弃IMF 个数的目的［3，4］，计算如式（1）：

根据式（1），结合EMD 分解原理，可以计算出具有噪声能量分布突变的第k 个IMF 分量，计算出k 值后，再舍弃前面高频相应的IMF 分量，重构剩余的IMF，因此实现对数据的去噪处理。其中，

为了得到噪声和主导信号的分界点k，即能量密度的全局极小值，定义全局极小值k 为：

根据式（3）确定出分界点k 后，由于在第k 个IMF 分量中有可能出现能量密度低于噪声分量的情况。为了消除这种影响，在确定分界点K 时，可以采取下列式子：

3.3 仿真实验

设原始信号为：

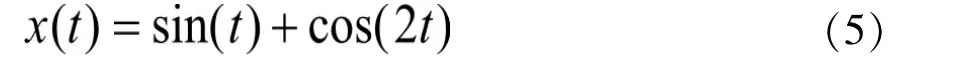
对上式信号添加高斯白噪声，信噪比为25dB，如图1：

经EMD 分解，IMF 分量如图2和图3。

经过连续均方误差方法计算，计算结果如表1所示。表中为各IMF 分量的均方误差，从高频到低频，第一个最小的均方误差出现在第2 个IMF，根据原理将局部极小值后移一位，从而重构第3 个至最后一个IMF 分量，如图4所示（蓝色是原始数据，红色是重构数据）。从图中可以直观地看出，重构数据在一定程度上能够重现原始数据的波动走势。据此，采用此方法在信号去噪种能够达到较好的效果。

3.4 实用分析

为了验证连续均方误差方法的实用性，本文选取文献1 中的岩心高光谱数据，数据波谱范围为350 纳米-2500 纳米，本小节各图中纵坐标为反射率（范围0-1），横坐标为波长（单位纳米）。

图1 原始信号以及加噪信号

图2 原始信号EMD 分解图

图3 加噪信号EMD 分解图

图4 高信噪比下EMD 去噪效果图

表1 各IMF 分量的连续均方误差

图5 本文去噪法信号重构图

图6 db8 小波去噪信号重构图

图7 db3 小波去噪信号重构图

需滤波信号为实测的方解石高光谱数据，经过连续均方误差方法处理，确定分界点舍弃对应的IMF 分量，重构剩余IMF 得到去噪信号，结果如图5所示。同时，利用小波方法将实测数据进行去噪，选取其中效果较好的db8 小波（图6）和db3 小波（图7）。图中蓝色曲线为原始信号，红色曲线为重构信号。

表2 不同方法去噪后信噪比

从表2的信噪比可以看出，在db3 小波去噪法下，去噪效果差，重构信号中局部波形发生畸变，这是因为有用数据中的突锋和突变部分由于小波去噪不具有自适应性，在滤波过程中被其当成噪声从而被平滑掉；db8 小波去噪效果优于db3 小波，但是由于相同原因，即也不具有自适应性，其去噪效果也较差。而本文采用的EMD 去噪方法根据信噪比，明显要优于小波去噪方法。从图中可以直观看出：本文采用的方法有效地去除了高光谱曲线由于各种原因污染的噪声，在消除毛噪现象的同时又保持了光谱曲线的各种特征，如吸收峰位置和吸收面积等，所重构的光谱曲线趋势特征几乎维持不变，准确的确定出了曲线突变或缓变的位置，且不用去考虑小波阈值去噪中关于怎么选择基函数，参数的设置等问题，可以看出，不管是去噪过程还是去噪结果，本文方法更佳。

4 结论

本文探讨了EMD 的滤波特性，在面对EMD 分解原理和小波去噪方法的局限时，采用了根据连续均方误差方法而确定分界点的EMD 重构去噪方法。EMD 分解后，信号有用成分主要位于低频IMF分量中，而噪声成分主要混叠于高频分量中，通过EMD 分解进行去噪，关键在于确定出信号与噪声的IMF 分量的最优分界点。根据本文中的数据和分析可以得出：连续均方误差方法无论是在去噪过程或去噪效果上，都比常用方法如小波去噪更佳。在去噪过程中，不用考虑基函数选取或参数设置的问题；在去噪结果上，在消除噪声尖峰和突变情况的同时，光谱曲线的各种特征又能得到很好的还原。因此，应用此方法可以更加方便地对各种信号，特别是非平稳或非线性的进行处理。

虽然从某种意义上说，噪声与有用信号分界点难以确定的问题，在此方法中得到了较好的解决。但是如果将本文方法应用在噪声污染严重情况下，此时就会出现有用信号能量太低的问题，这是由于原始信号噪声污染严重所致，从而就会使噪声在各IMF 上的分布规律基本一致，因此应用此方法可能不能找出全局极小值；即使全局极小值存在，起主导作用的信号由于污染严重的噪声干扰也不能确定一定是噪声，从而使得舍弃对应个数的高频IMF 的同时也会导致有用信号的丢失。