Lagrange中值定理的证明及其应用

肖 琪 龚 萍

（攀枝花学院数学与计算机学院 四川·攀枝花 617000）

微分中值定理（主要包括Rolle中值定理、Lagrange中值定理和Cauchy中值定理等）是微分学中的基本定理，而Lagrange中值定理是最为重要的定理，Rolle中值定理是其基础和特殊情况，Cauchy中值定理是其推广，Lagrange中值定理可用于研究函数的单调性、凹凸性及其连续性等性质、等式证明、不等式证明、级数敛散性判别以及求函数极限等方面。本文主要研究Lagrange中值定理的证明，以及在等式证明、不等式证明和求函数极限这几方面的应用，通过具体的例题来分析、归纳和总结对应题型的解题思路、方法与步骤。

1 Lagrange中值定理

1.1 Lagrange中值定理

1.2 Lagrange中值定理的证明

人们经常通过借助辅助函数，利用积分法、几何法、待定系数法、分析法、推论法等方法来Lagrange中值定理的证明。下面通过倒推法来构造辅助函数，其主要过程为：

（2）将等式两端简单积分，不考虑常数c：

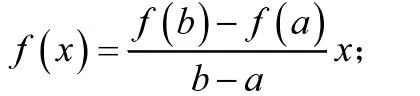
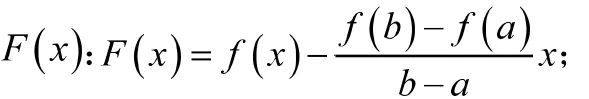
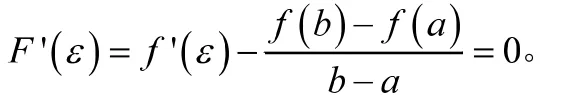
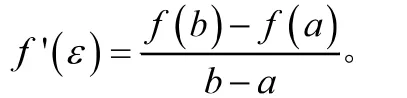
2 Lagrange中值定理的应用

本节中，我们将通过具体例子，阐述说明Lagrange中值定理在证明等式、证明不等式和求函数极限中的应用，通过具体的例题来分析、归纳总结对应题型的解题步骤、方法。

2.1 证明等式

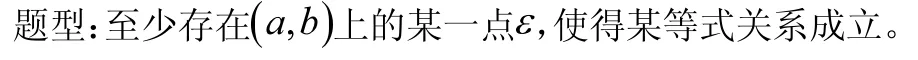
2.2 证明不等式

题型：如果需要证明的不等式中涉及某一个函数的两点函数值之差的。

2.3 求函数极限

题型：所求函数极限中为同类型函数的两点函数值之差，且自变量仅相差一个常数。

3 结束语

本文主要研究了Lagrange在证明等式、证明不等式和求函数极限中的应用，Lagrange中值定理还可用于研究级数敛散性、函数单调性和凹凸性等性质，但归根结底，其重点在于构造辅助函数。可见，Lagrange中值定理是学好微分学、高等数学的重中之重，要学好、用好Lagrange中值定理需要对其核心内容及其特点做到能够灵活运用，并且归纳总结其特性以及思想方法。