发展学生思维的小学数学教学思考

孟庆军

摘  要：着眼于数形结合、情境直观、实践操作落实的有效教学能够很好地帮助学生理解所学内容并获得思维的发展，教师应善于落实注重直观、多管齐下的有效教学并帮助学生获得思维瓶颈的有力突破。

关键词：数形结合;情境直观;实践;理解;思维

通过数形结合、情景直观、动手操作等手段为学生搭建思维发展的脚手架，能帮助学生突破思维发展的瓶颈并获得数学能力的发展。

一、形、式结合促理解

数学研究对象并不都是直观呈现的，很多“看不见、摸不着”的数学研究对象对于学生而言抽象而空洞，但这些抽象的数学研究对象在根、源上却一定有其具体的体现。教师引导学生借助图形对这些抽象的数学研究对象进行思考与想象，能使复杂问题变得简单，学生在形象生动的研究对象的探索中也更易获得正确而深刻的理解 [1]。

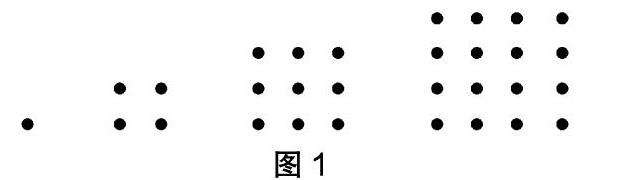
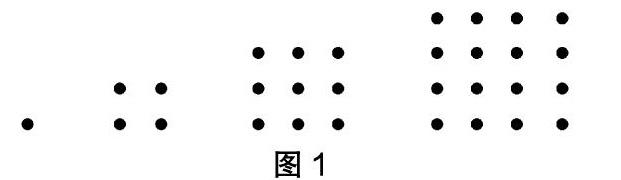
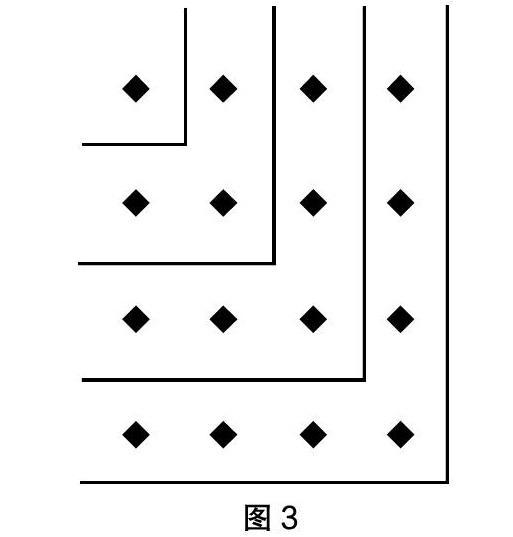
比如，教材借助了四个正方形点阵对“点阵中的规律”这一内容进行了呈现，旨在引导学生对四个点阵中所隐含的规律进行探索、计算与归纳，并因此在获得规律的经验中得出第五个点阵并说出其中所含点的数量。教材对这一内容的设计主要是为了引导学生在多样化的点阵研究形式中获得知识与体悟。但很多学生因为抽象思维能力的不足很难体会更多的形式。因此，教师可以在具体教学中借助数形结合的形式来帮助学生加深对这一内容的理解与体会。片段如下：

投影练习：找规律。将教材中“1，4，9，16，（   ），（   ），”作为找规律的最后一个练习题，引导学生在图1所示的正方形点阵图中初步发现第几个点阵的点数能用几乘几进行表达，这是建立在学生已有经验基础上的设计。

二、情境直观促提升

能够发展学生观察能力的直观情境能使学生更好地将表象与概念联系在一起并获得视觉、听觉、感受与思维的同时提升。因此，教师应根据教学内容与学情设计合理的生活情境，使学生从形象过渡到抽象并获得形、神的同步发展 [2]。

比如，我校某教师在数学教研活动中就设计了“站一站”的活动来帮助学生对“重叠问题”进行理解。片段如下：

师（取出准备好的天鹅、蝴蝶、金鱼、海豚等七种不同的动物头饰和两个呼啦圈，请七位学生进行“站一站”的游戏）：请会飞的和会游泳的分别站到蓝色和黄色的呼啦圈内。（有两位学生先后站在了蓝色与黄色呼啦圈内）

师：有两位同学先后站在了两个圈内，大家发现了吗？你们认为他们这么做的理由是什么呢？他们应该怎样站才能准确表达老师提出的要求呢？（两位学生均把自己的两只脚分开并分别站在了两个圈内）

师：大家觉得他们把两脚分开并分别站在两个圈里表达的是什么意思呢？

生：表示会飞也会游。

师：这两位同学真聪明，你们两位可以把呼啦圈抬起来让大家都看清吗？（学生无法完全抬起呼啦圈）

师：有没有更好的办法来表达这两位同学的意思呢？

生：可以将两个呼啦圈交叉出公共部分并让他们站在这个公共部分里。

师：有谁来演示一下？（有学生自告奋勇上前进行演示，直观的韦恩图因此呈现）

韦恩图能简洁明了地表达集合、集合与集合之间的关系，但其抽象过程并不是很好理解，教师所设计的“站一站”游戏使学生在热情的活动中获得了真实、形象的体会，学生的思维活动在变得积极热烈的同时也很好地完成了形、神结合的教学活动。

三、实践中实现理、法的有效对接

学生在动手操作中往往能够调动各种感官，对事物进行多角度的观察，在建立丰富表象的同时能使其思维活跃而发展迅速 [3]。新课标早就确立了“动手实践”这一学习方式的重要地位，事实上，教师采取这一重要方式落实教学活动也确实取得了很好的教学效果。

笔者在“两位数除以一位数、商是两位数”这一内容的教学中设计了“分桃子”这一教学活动。片段如下：

师：68÷2等于多少？应该怎样计算呢？我们一起来研究一下这一计算的方法吧。

生1：我觉得可以口算解决，将68拆成60与8，60÷2=30，8÷2=4，30+4=34。（配合课件展示）

师：很好，口算解决这一问题也是一种方法，大家还有其他办法吗？

生2：我是根据题中的图片来计算的，先看整篮的桃子，每只猴子可得3篮即30个桃子，还有8个桃子平均分给两只猴子，每只猴子4个桃子，因此每只猴子可得34个桃子。（配合课件展示）

师：口算与看图分桃可以计算出68÷2等于多少，还有其他办法吗？

生3：竖式计算也可以。

师（板书“竖式”二字）：大家从口算与看图分桃的过程可以得出68÷2的竖式吗？首先我们来回想一下口算的第一步是算的什么，看图分桃的时候第一步又做了什么呢？

生1：口算的第一步是算60÷2=30，看图分桃的第一步也是从整篮桃子的分法上着手的。（配合课件进行动态展示）

师：那么，我们应该怎样用竖式表示口算和看图分桃的第一步呢？

生2（邊写边说）：首先用十位上的6除以2，得到商3之后将其写在被除数十位上面，然后再用3乘2得到6，即6个十，此时意味着已经分掉了6个十，6个十减6个十即为0。

师（追问）：大家想想看，此处的0要不要写呢？

众生：不用，除法还没做完呢。

师：很好，那么大家再想想口算与看图分桃的第二步又是如何进行的呢？

生3：口算第二步为8÷2=4，看图分桃的第二步是把剩余的8个桃子平均分给了2只猴子，每只猴子得到4个桃子。（配合课件进行动态展示）

师：很好，接下来谁来完成口算与看图分桃的竖式计算第二步呢？

生4（边写边说）：将个位上的8落下并除以2可得商是4，将4写在被除数个位上面后再用4乘2可得8，说明又分了8个桃子，8减8等于0。

师：这里的0要写吗？

众生：要写！

行为表征、表象表征、符号表征是认知所经历的一般过程，表象操作在直观操作到一般算法的过程中能够起到至关重要的作用，教师在具体教学中如果忽略这一环节，学生在竖式计算的学习上就和直观操作脱节了。笔者在学生完成小棒摆放的过程后及时将这一实践操作与竖式计算步骤进行了整合，使学生在形象与抽象的整合连接中顺利地实现了从具体到抽象的过渡 [4]。

教师在具体教学中应好好把握促进学生思维发展这一重要的教学目标，着眼于数学学科的特点、学生的年龄特点以及思维发展的规律进行教学，使学生能够在注重直观、多管齐下的有效教学中获得思维瓶颈的有力突破。

参考文献：

[1]  黄晓学. 论思维生惑点与数学教学[J]. 数学教育学报，2007，16（2）：16-19.

[2]  温建红. 论数学课堂预设提问的策略[J]. 数学教育学报，2011，20（3）：4-6.

[3]  章建跃. 构建逻辑连贯的学习过程使学生学会思考[J]. 数学通报，2013，56（6）：5-8，封底.

[4]  黄艳玲，喻平. 对数学理解的再认识[J]. 数学教育学报，2002，11（3）：40.