高中生核心素养之“数学建模”能力的培养与思考—以“建立数列模型解决实际问题”教学为例
2019-04-10广东省广州市番禺区石楼中学511447梁振强
广东省广州市番禺区石楼中学(511447) 梁振强
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型、用数学知识解决问题的素养,是学生高中阶段必备的数学核心素养之一.《普通高中数学课程标准(2017年版)》明确指出:“数学核心素养是数学课程目标的集中体现,是在数学学习的过程中逐步形成的.高中阶段数学核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数学分析.”其中,更是强化了数学建模思想的核心地位,并以主题的形式要求学生参与数学建模活动与数学探究活动的全过程,使学生认识数学模型在科学、社会、工程技术诸多领域的作用,提升实践能力、增强创新意识和科学精神.
笔者认为,要想提高学生核心素养,首先要提高学生数学建模能力.如何在高中数学课堂教学中渗透数学模型核心素养能力的培养,值得一线数学教师实践与思考.下面以“建立数列模型解决实际问题”的教学为依托,浅谈一下学生核心素养的根植与培养.
一、教学内容与目标
1.教材和学情分析
本节课是对普通高中新课程标准实验教科书《数学5》(人教A版)第二章《数列》中2.2节—2.5节内容进行整合而形成的一节实际应用课,主要内容是通过对日常生活中的两个实例分析,得到等差、等比两种数列模型以及建立数列模型的具体步骤.数列作为一种特殊的函数,是反映自然规律的基本数学模型,等差、等比数列又是数列中最特殊的两种数列,在日常生活中有着广泛的应用.本节课是关于等差、等比数列及其求和公式实际应用的一节整合课,是本章内容的升华,目的是让学生感受这两种数列模型应用的广泛性,并能够利用它们解决生活中的实际问题.
学习本节课之前,学生已经对等差、等比数列的概念及其前n项和公式有了较深的认识,这对建立这两种数列模型做好了知识储备.从认知结构方面,大量的数学思维方法如类比思想、归纳思想、数形结合思想、方程思想等已为学生所习知.但在分析问题的实际背景、明确问题的复杂条件等方面还有一定的困难,尤其是用函数的背景和研究方法来认识、研究数列,还没有形成思维习惯,所以“建模”和“解模”两步对学生来说还是个难点.
2.教学目标
要解决日常生活中有关数列的问题,必须从实际情境中抽象出相应的数列模型,进而转化成数学问题求解.基于以上学情分析,本节课的教学目标如下:
(1)学会解决有关等差数列模型的实际问题.
(2)学会解决有关等比数列模型的实际问题.
(3)明确建立数列模型的步骤.
教学重点:建立数列模型的步骤,解决有关等差、等比数列模型的实际问题.
教学难点:从生活背景中提炼出相关的数量关系,将现实问题转化为数学问题,构造等差、等比数列模型,并加以解决.
二、主体教学过程设计
(一)回顾旧知
问题1 等差、等比数列相关知识的复习.
问题2解决应用问题的思路.
教师活动:提问与引导;
设计意图让学生更加熟悉数列建模的必备知识并懂得数学知识的系统性与关联性.
(二)实例情境1
假设某市2013年新建住房400万平方米,其中有250万平方米是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2013为累计第一年)将首次不少于4750万平方米?
(2)当年建造的中低价房的面积占建造住房面积的比例首次大于85%?
设计意图以实际生活实例让学生感受建立两种特殊数列模型的方法和步骤.
问题1 描述中低价房的关键信息是什么?它的数学实质是什么?如何把第(1)问转化为数学问题?
教师活动:多重设问引导学生提炼关键信息,板书建模解模步骤;
设计意图使学生很自然地从实际情境中抽象出等差数列模型并明确“建模”步骤:设→建→解→答.
问题2 描述新建住房的关键信息是什么?它的数学实质是什么?如何把第(2)问转化为数学问题?
教师活动:提问并组织学生交流解题过程;
设计意图培养学生从实际情境中抽象出等比数列模型的能力.
问题3 解模中的不等式“n+4>6.8×1.08n-1”能否用数形结合的方法?
教师活动:用几何画板演示.
设计意图通过数形结合的方法使学生进一步理解数列是一种特殊函数.
问题4“每年新建住房面积平均比上一年增长8%”和“中低价房的面积比上一年增加50万平方米”的数学实质是什么?
设计意图强化学生“识模”即“抓关键信息”的能力,总结建模的步骤:识模→建模→解模→答模,从而突出重点.
(三)实例情境2
某家庭打算在2013年的年底花40万购一套商品房,为此,计划从2007年初开始,每年初存入一笔购房专用款,使这笔款到2013年底连本带息共有40万元.如果每年的存款数额相同,依年利息2%并按复利计算,问每年应该存入多少钱?(1.027≈1.1487)
设计意图实践建模方法过程.
问题5 题目中的关键信息是什么?它的数学实质又是什么?
设计意图训练学生抓关键信息、分析关键信息的能力.
问题6 从2007年到2013年共存了几次钱?每次存的x万元到2013年底的本利和分别是多少?如何把这一问题转化为数学问题?
设计意图明确数列中的计数问题,亲历建立等比数列模型的方法,重视解模答模的过程,从而突破难点.
(四)目标检测
目标检测题1某市一家商场的新年最高促销奖设立了两种领奖方式,获奖者可以选择2000元的奖金,或者从12月20日到第二年的1月1日,每天到该商场领取奖品,第1天领取的奖品的价值为100元,第2天为110元,以后逐天增加10元,哪种领奖方式获奖者受益更多?你会选择哪种方式?
目标检测题2一名体育爱好者为了观看2016年里约热内卢奥运会,从2010年起,每年的5月1日到银行存入a元一年期定期储蓄,假定年利率为p(利息税已扣除)且保持不变,并约定每年到期存款均自动转为新一年的定期,到2016年5月1日将所有存款和利息全部取出,则可取出的钱的总数是( )
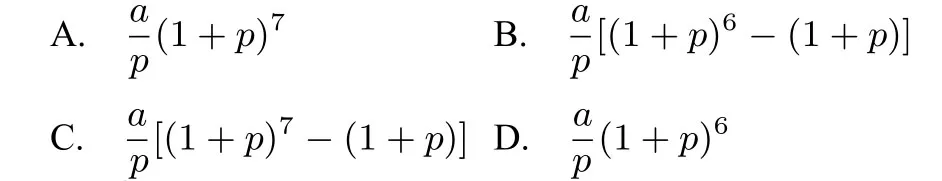
设计意图了解建立等差数列、等比数列模型的达成情况.
三、教学思考
数学建模素养作为主要的核心素养,加强其在平常教学中的渗透尤为重要.教师要善于发挥教学的主导和引领作用,促进数学建模素养的落实.新颁布的高中数学课程标准修订稿将数学建模素养划分为三个水平,并且有十分详细的描述,如了解熟悉的数学模型的实际背景及其数学描述,了解数学模型中的参数、结论的实际含义;能够在熟悉的情境中发现问题并转化为数学问题,知道数学问题的价值与作用;能够在综合的情境中,运用数学思维进行分析,发现情境中的数学关系,提出数学问题等.教师的教学活动应基于数学核心素养而进行,特别是针对三个水平展开对学生数学建模素养的培养.
(一)丰富课堂阅读材料,为学生的数学建模思想应用奠基.教师应为学生提供丰富的阅读材料,让学生多接触实际生活中的数学问题,了解所熟悉的数学模型的实际背景及其数学描述,从而为学生用数学模型解决现实问题积累经验.
(二)组织学生开展数学建模活动,培养学生的数学能力.通过开展数学建模活动,可以让学生经历发现问题、解决问题的过程,进而体会数学建模的思想和方法.在数学建模活动中,通过讨论式的教学方法,让学生参与到教学环节中,充分发挥学生的主体作用.
(三)从日常教学抓起,促进学生的综合发展.在教学中不断引导学生会学习、会思考、会应用,能够用数学的思维方式去观察、分析和表示实际问题中的各种度量关系和位置关系,从纷繁复杂的具体问题中抽象出数学信息并建立数学模型,进而达到用数学模型来解决实际问题,使数学建模意识成为学生思考问题和解决问题的习惯,在数学教学中进行主题式教学设计和实施,让数学建模素养真正落地.
四、结语
重视培养学生数学建模的能力已成为数学教育界的共识,在新课程改革的稳步推进中,数学建模将逐步成为数学教育者关注的重点议题.通过数学模型教学案例探析教学活动,学生的数学运算、逻辑思维能力、数学分析等几个核心素养在模型建构中也会有充分的体现,应用数学的意识肯定能得到逐步增强.可以说六大核心素养是蕴含在模型建构教学的整个过程中的,因此应当重视学生的数学建模能力,发展学生的应用意识,从而将学生的数学核心素养落实到位.
