从目标定位到目标达成的观察与思考*—例谈高中数学概念课渗透核心素养培养

广东省广州市花都区圆玄中学(510800) 罗莉萍

课堂设计要科学必须思考如何渗透核心素养的培养.核心素养强调的是”养”,一般指的是”素质和修养”,即在先天生理特点基础上,经由”后天”学习形成的”知识、能力、态度”的综合体现.下面我以一节课为例谈谈从课堂教学目标定位到目标达成的观察与思考.

近日我听了M老师的一节区公开课,内容是高一必修二的《3.3.1两条直线的交点坐标》.这节课,从表面上看挺顺畅的,学生上黑板演示展示也比较多,但听完课,同行老师都一致觉得这节课平淡、乏味,整一节课就只是在解方程组,缺少生成,无令人怦然心动的教学片断.为什么会出现这种现象呢?

为了找到更科学合理的解析,我与大学在校生针对这节课做了深入交流,她站在学生所需核心素养角度,我站在教师开启学生核心素养角度去思考这节课,并提出修改建议.

首先必须是让学生明确概念,这节课的概念不难理解：两条直线的交点就是两条直线的公共点,其坐标满足两直线方程.教师正是直接梳理概念后就进入了解方程组的状态.

我们从两个关注、八个角度对这堂课进行观察与分析.

两个关注：一是关注知识的传授,是否为高认知水平；二是关注学生的发展,是否为高参与度.从这节课表面上看,学生的参与度是比较高的,但认知水平偏低了,整一节课就只是在解方程组,无思想高度,平淡、乏味.

八个角度：内容设计、教学表述、进度安排、资源利用、激发动机、师生互动、自主学习、鼓励创新等.从这节课表面上看,大部分视角都没有问题,但在内容设计和鼓励创新上做得不够好,所以缺少生成,无令人怦然心动的教学片断.

也就是说这节课的问题在高认知水平和内容设计上,也就是教学设计出了问题,而教学设计的关键之处是对目标设计思考和对目标达成思考.

一、对目标设计的思考

教学目标设计很重要,因为教学资源的选择、教学策略的选择、教学实施、教学评价都要围绕教学目标进行.合理进行教学目标设计,就是要将数学核心素养要求融入课堂教学目标,为了合理设计教学目标教师要做好四个方面：目标分解、任务分析、起点确定、目标表述.

1、目标分解要合理

M老师觉得这节课的目标分解主要是分三步：一是能建立直线上的一个点与二元一次方程的一组解之间的对应关系；二是能建立二元一次方程组的解与两直线位置关系之间的对应关系；三是会求两条直线的交点坐标.

我们先看章节内容安排：

《3.3.1两条直线的交点坐标》在3.2直线方程之后进行学习的.“能建立直线上的一个点与二元一次方程的一组解之间的对应关系”应该是3.2直线方程的主要教学目标之一,是学生的起点能力而非这节课的教学目标.这节课的目标分解主要是分两步：一是能建立二元一次方程组的解与两直线位置关系之间的对应关系；二是会求两条直线的交点坐标.

对3.2直线方程学习不仅使学生“知道直线方程的代数特征是二元一次方程”,还要求学生“能建立直线上的一个点与二元一次方程的一组解之间的对应关系”.目标分解不合理,教学容易偏离重心,将起点能力定位成教学目标,会降低认知高度.

2、任务分析要清晰

由于要将“能建立直线上的一个点与二元一次方程的一组解之间的对应关系”划分、融合到学生的起点能力部分.这节课的使能目标分析要做以下修改：

3、起点确定要准确

任务分析可见这节课的学生的起点能力分析：

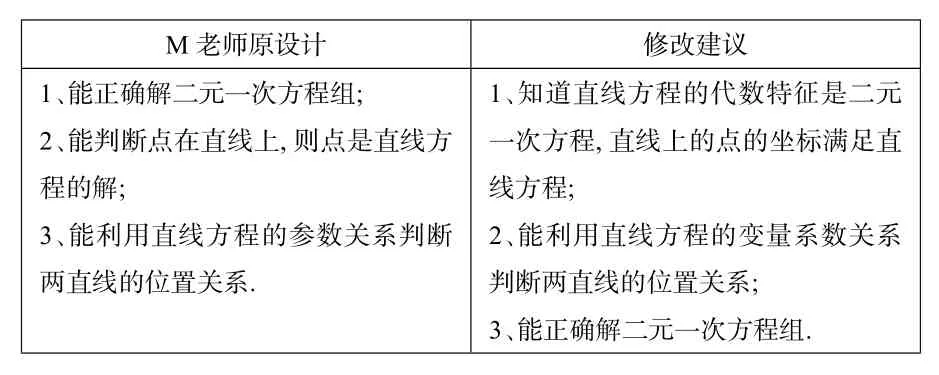
M老师原设计修改建议1、能正确解二元一次方程组；2、能判断点在直线上,则点是直线方程的解；3、能利用直线方程的参数关系判断两直线的位置关系.1、知道直线方程的代数特征是二元一次方程,直线上的点的坐标满足直线方程；2、能利用直线方程的变量系数关系判断两直线的位置关系；3、能正确解二元一次方程组.

4、目标表述要具体、明确

M老师原设计修改建议教学目标：1、能建立直线上的一个点与二元一次方程的一组解之间的对应关系；2、能建立二元一次方程组的解与两直线位置关系之间的对应关系；3、会求两条直线的交点坐标.教学目标：1、能建立二元一次方程组的解与两直线位置关系之间的对应关系；2、会求两条直线的交点坐标.

M老师的目标定位是没有太大问题的,问题到底在哪?看来问题主要在从课堂教学目标定位到目标达成这个环节上.

二、对目标达成思考

1.要重视情境创设

要用实际问题驱动思考.数学知识的学习讲究顺势而为,它是经验的结果,更是思考的结果.经过对学生的起点能力分析发现,这节课学习的支持性条件有三条,课前必须加以夯实.

教学过程1

M老师原设计修改建议一、情境导入已知直线l的方程为2x-y+3=0,(1)点(1,5),(3,8)在直线上吗?(2)点(2,y)在直线上,则y=一、限时训练1、已知直线l经过点A(-1,1),B(2,7),(1)直线l的一般方程为..(3)点(x,5)在直线上,则x=.～二、导学探究判断下列各对直线是否相交：(1)l1∶3x+4y-2=0,l2∶2x+y+2=0.(2)l1∶2x-6y+3=0,l2∶y=1(2)点C(1,5),D(3,8)在直线上吗?为什么?(3)若点 E(2,y)、F(x,5)在直线上,则y=；x=.(3)l1∶2x-6y=0,l2∶y=1 3x+1 3x+1 2.2.2、判断下列各对直线的位置关系.(1)l1∶x-y=0,l2∶3x+3y-10=0.(2)l1∶3x-y+4=0,l2∶6x-2y-1=0.(3)l1∶3x+4y-5=0,l2∶6x+8y-10=0.

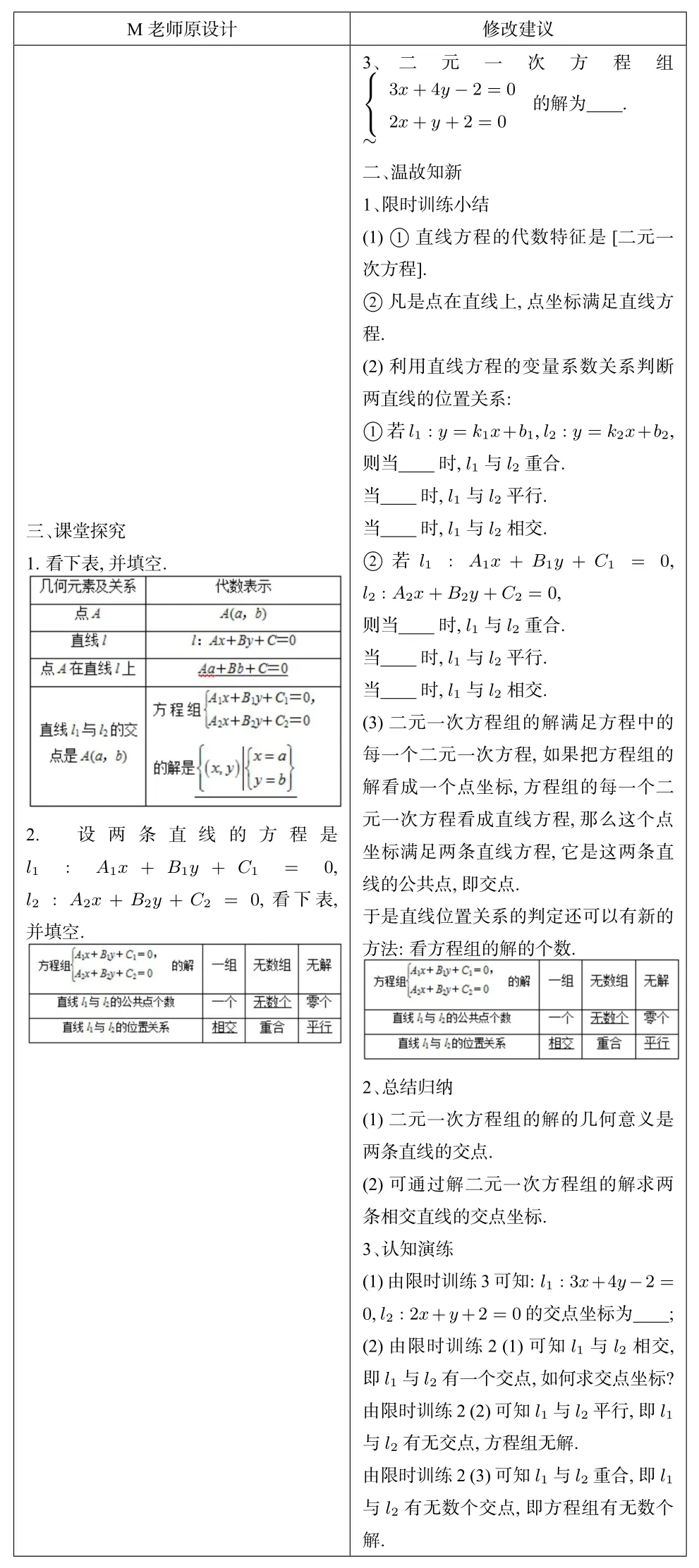
M老师原设计修改建议3、 二 元 一 次 方 程 组3x+4y-2=0 2x+y+2=0 的解为.～时,l1与l2重合.当二、温故知新1、限时训练小结(1)①直线方程的代数特征是[二元一次方程].②凡是点在直线上,点坐标满足直线方程.(2)利用直线方程的变量系数关系判断两直线的位置关系：①若l1∶y=k1x+b1,l2∶y=k2x+b2,则当时,l1与l2平行.当 时,l1与l2相交.②若l1∶A1x+B1y+C1=0,l2∶A2x+B2y+C2=0,则当三、课堂探究1.看下表,并填空.时,l1与l2重合.当时,l1与l2平行.当 时,l1与l2相交.(3)二元一次方程组的解满足方程中的每一个二元一次方程,如果把方程组的解看成一个点坐标,方程组的每一个二元一次方程看成直线方程,那么这个点坐标满足两条直线方程,它是这两条直线的公共点,即交点.于是直线位置关系的判定还可以有新的方法：看方程组的解的个数.2.设两条直线的方程是l1∶A1x+B1y+C1= 0,l2∶A2x+B2y+C2=0,看下表,并填空.2、总结归纳(1)二元一次方程组的解的几何意义是两条直线的交点.(2)可通过解二元一次方程组的解求两条相交直线的交点坐标.3、认知演练(1)由限时训练3可知：l1∶3x+4y-2=0,l2∶2x+y+2=0的交点坐标为 ；(2)由限时训练2(1)可知l1与l2相交,即l1与l2有一个交点,如何求交点坐标?由限时训练2(2)可知l1与l2平行,即l1与l2有无交点,方程组无解.由限时训练2(3)可知l1与l2重合,即l1与l2有无数个交点,即方程组有无数个解.

M老师的原设计和“修改建议”都注重了创设情境.即通过一些已知的题入手,引导思考,突出问题导向.

对比两者,虽然都关注到起点能力这三条学习的支持性条件,但是M老师的原设计问题导向方面做得不是很好,思考不够深入,比较空洞,概括总结力度也不够.

2.要注重整体把握

“修改建议”中的限时训练与起点能力这三条学习的支持性条件一一对应,它不仅是为了“温故”,更重要的是为了“知新”,在夯实基础的过程中引导学生发现新知,其认知水平较高,因势利导做得比较好.认真观察,“修改建议”中的限时训练2和3与教材的两个例子相关,认知演练其实就是解决课本的例1和例2,弹性使用教材,还最大化地发挥教材题例的价值,使学生在不知不觉中完成新知学习,真可谓“润物细无声”.

教学要注意突出内容主线,“修改建议”从限时训练引入到温故知新,再到下面的典例精析,都是浑然一体,一气呵成的.

教学过程2

M老师原设计修改建议四、典例精析例1.求下列两直线的交点坐标,l1∶3x+4y-2=0,l2∶2x+y+2=0.例2.判断下列各对直线是否相交,如果相交,求出交点坐标.(1)l1∶x-y=0,l2∶3x+3y-10=0.(2)l1∶3x-y+4=0,l2∶6x-2y-1=0.(3)l1∶3x+4y-5=0,l2∶6x+8y-10=0.～五、拓展训练1.求过两直线3x+4y-2=0和2x+y+2=0的交点且过坐标原点的直线l的方程.2.求过两直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线l方程.三、典例精析例1.过点 A(1,2)引直线l∶2x-3y+10=0的垂线,求垂足坐标.例1变式.已知点A(1,2)、B(-3,1),求过A与直线AB垂直的直线与直线2x-3y+10=0相交的交点坐标.例2.若l1∶ax+2y+8=0,l2∶4x+3y=10的交点在l3∶2x-y=10上,求a值.

这节课的核心是求两条直线的交点坐标,而M老师的原设计中的拓展训练的两题主语都是求直线方程,虽然涉及了直线交点问题,但对核心的体现就不是很好.

对比两者,M老师原设计的典例精析部分,“修改建议”早已通过温故知新的形式完成了,显然“修改建议”的思维高度和能力要求比M老师的原设计高.

3.要注意追求思想

单纯地搞好教学目标设计是不够的,在目标指引下还要充分展示教学智慧,数学教学不能仅仅停留在知识层面,更要体现数学思维,即要注意追求思维与能力的提升,这其实就是学生核心素养的提升.

M老师的原设计只体现了方程思想,教师是很难展开的,这就不难理解为什么听课老师觉得“整一节课就只是在解方程组,无思想高度,平淡、乏味”.“修改建议”突出这节课的核心是求两条直线的交点坐标.而且会有多种方法生成：

例1过点A(1,2)引直线l∶2x-3y+10=0的垂线,求垂足坐标.

方法一顺题意操作,先求垂线方程,然后联立方程求垂足坐标.

方法二待定系数法.设垂足为B(m,n),引导学生挖掘几何特征：①由l⊥AB得②由B在直线l上得2m-3n+10=0.联立方程求m、n.

同理,例1的变式也一样可以一题多解,学生可以选择适当的方法解决问题.

修改建议中除了方程思想,还有数形结合思想.这样更能突出解析几何学习的本质,解析几何使用代数思想解决几何问题,它的表现是代数,它的本质关键是几何特征.

4、要注意揭示本质

教师的责任是把数学的学术形态化为教育形态,不但要使学生容易接受,还要注意揭示数学本质,提升学生数学素养.例如“修改建议”中的例2.

例2若l1∶ax+2y+8=0,l2∶4x+3y=10的交点在l3∶2x-y=10上,求a值.

方法一顺题意操作,先联立l1、l2方程求交点坐标,求得的交点坐标含参数a,然后代入l3∶2x-y=10,求a值.

方法二依题意,作简图发现l1、l2、l3相交于一点,先联立l2、l3方程求交点坐标,求得的交点坐标不含参数,代入l1∶ax+2y+8=0,可求a值.

比较两种方法比较,方法二较佳.方法二的来源是能够很好地揭示题目的几何特征.

这个例子的设计能使教师很好地处理预设与生成的关系,容易启发引导,帮助学生理清思路.

一节好课必须能看到学生的生成,其实就是能看到学生核心素养的培养.一节课的成功除了目标定位准确外,从课堂教学目标定位到目标达成这个环节也很重要,这需要教师有扎实的数学专业知识,知道知识的核心思想,知道知识的来龙去脉,且善举例、善质疑、善优化.总之,教师要立足于学生的认知基础、立足于培养学生核心素养,这样才能真正上出令人回味的优质课.