培养解题步骤的严谨性提升学生的解题能力—从一道高考题引出的思考

广东省佛山市南海区第一中学(528000) 黄森宏

在高中增加导数这部分内容之后,解决函数问题得到了很大的提升,方法也简单明了,使学生能以导数为工具研究函数的性质及函数图像等提供了更有效的途径和简单明了的操作手段,使学生对函数有更深刻的理解和直观的认识.多年来全国各地的高考试卷中有关导数部分的题目,题目的位置放在第21题,题目的总体难度对于学生来说比较大,但只要我们掌握函数与导数的基本思想,导数在函数研究中的地位与作用,以及恰当有效的解题方法步骤,是可以让学生比较好地解决这类问题的,强调步骤的严谨性,正是解决此类问题的关键.

高考导数试题的设计,一般是从以下几方面入手：①求函数单调区间,比较两个式的大小,考查不等式解法；②求函数的极值与最值；③利用导数几何意义构造几何量的最值问题；④以导数方法为前提设计实际综合问题,把导数灵活渗透在各个知识点上,同时要让学生(老师)根据问题去提炼出试题考查的目标是什么.

依据多年的教学经验,我们要做的就是培养学生的解题严谨性,提升学生的解题能力.经多年的教学经验,结合函数与导数的知识特性,总结出解此类问题的方法步骤如下：

①求函数的定义域

②求函数的导数

③令导数为零求出它的根,此时可能对有没有根进行分类讨论

④判断根把定义域分成多少部份,此时可能要对根的大小,根与定义域的关系进行讨论,通过列表去判断函数的单调性,同时强调表格中第三行其实就是函数的大致图像.

⑤通过表格的第三行再画出较为清晰的函数图像,(当然此图像只反映单调性)通过图像说明极值或最值在哪里

⑥极值的应用,它主要有三方面的应用,一求最值二判断函数零点三不等式的证明等等.此时对函数的图像有更高有要求,要求极值或最值的正负或者说它们的位置高度在哪,都要准确的画出来.例设函数f(x)=(x-1)ex-kx2(k∈ℝ).(1)当k=1时,求函数f(x)的单调区间；

(2)当k∈时,求函数f(x)在[0,k]上的最大值M.

解(1)当k=1时,f(x)=(x-1)ex-x2,f′(x)=ex+(x-1)ex-2x=x(ex-2),令f′(x)=0,解得x1=0,x2=ln2＞0,所以f′(x),f(x)随x的变化情况如下表：

x (-∞,0)0(0,ln2)ln2(ln2,+∞)f′(x)+0-0+f(x)↗极大值↘极小值↗

函数的大致图象如下：

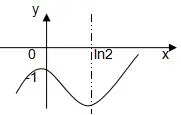
图1

所以函数f(x)的单调增区间为(-∞,0)和(ln2,+∞),单调减区间为(0,ln2).

(2)f(x)=(x-1)ex-kx2,x∈[0,k],k∈f′(x)=xex-2kx=x(ex-2k),f′(x)=0,解得x1=0,x2=ln(2k).

图2

令φ(k)=k-ln(2k),k∈所以φ(k)在上是减函数,所以φ(1)≤φ(k)＜φ

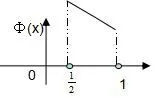
图3

所以1-ln2≤φ(k)即0＜ln(2k)＜k,所以f′(x),f(x)随x的变化情况如下表所示：

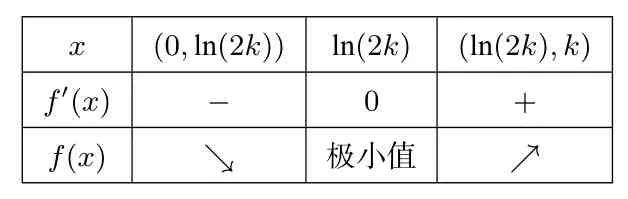
x (0,ln(2k))ln(2k)(ln(2k),k)f′(x)-0+f(x)↘极小值↗

函数的大致图象如下：

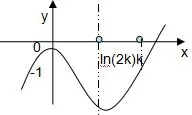
图4

以下比较f(0)= —1与f(k)=(k-1)·ek-k3的大小：令h(x)=(x-1)·ex-x3+1,(1 2＜x≤1).h′(x)=x·ex-3x2=x(ex-3x).令g(x)=ex-3x,则g′(x)=ex-3＜0,φ(x)单调递减,g(1)=e-3＜0,存在唯一的x0∈使g(x)=0.所以在上h′(x)＞0,h(x)递增；在 (x0,1)上h′(x)＜0,h(x)递减.而hh(1)=0,故h(x)≥ 0,即f(k)≥-1.所以M=f(k)=(k-1)·ek-k3.

函数与导数是高中学子们学习的重点与难点,很多学生因为不了解或者没掌握好函数与导数问题的解决方法,往往无从下手,所以我们更要紧扣导数是研究函数性质的一个非常好的工具,掌握导数作为解题工具的方法与实质,掌握解题步聚,必能一层一层抽丝剥茧,化解难点,达到解决问题!