一道教材中“拓广探索”题目的变式与探究

广东省珠海市九洲中学(519015) 卢文彬

爱因斯坦曾说过,提出问题比解决问题更可贵,教师通过捕捉学生作业里创新学习生成的问题进行教学创新设计,既能激发学生的大胆猜想,提高学生深度学习数学的兴趣,让数学学科的核心素养真正落实,还能启发教师对教材的深度钻研,提高教师创新教育的专业素养,下面就学生作业里提出的一个问题进行案例分析.

一、提出问题

例 1 如图1,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证：AE是∠DAB的平分线.(题目来源于2013人教版数学八年级上52页第7题)

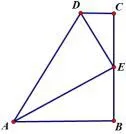
图1

二、分析问题

做几何证明题,通常有两种方法：从条件入手或者从结论入手,即综合法及分析法.综合法是指在推理的过程中,从已知开始,一环扣一环,最后导致所要证明的结论成立,即从已知看可知,逐渐靠拢未知的一种证明方法,此法是我们证题的常用方法.分析法是指从要证的结论出发,逐步寻求使它成立的充分条件,直到推出一个正确的条件,如已知、定理、性质等,即从未知看须知,逐渐靠拢已知,从而达到证明.

这道题目如果从条件入手可以发现：已知DE平分∠ADC,且∠C=90°,由此可以初步确定,要用角平分线的性质(角平分线上的点到角两边的距离相等)来做辅助线,这也和教材中对本题的提示相吻合,这是本题的解法一.

另外题目中有条件：∠B=∠C=90°,E是BC的中点,所以可以通过延长AE或延长DE,通过构造全等三角形来证明,这也是对应的解法二及解法三.

三、解决问题

解法一(利用角平分线的性质做垂线)

证明如图2,过点E作EF⊥AD,垂足是F.因为DE平分∠ADC,且∠C=∠EFD=90°,所以CE=EF,又因为E是BC的中点,所以EB=EF.在 Rt△AEF和 Rt△AEB中,因为AE=AE,EB=EF,所以△AEF～=△AEB(HL),所以∠BAE=∠FAE,即AE是∠DAB的平分线.

图2

解法二(利用平行线的性质延长线段)

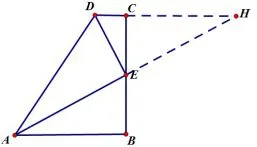
图3

证明如图3,延长AE及DC,相交于点H.在△ABE和△HCE中,因为∠B=∠ECH,∠BEA=∠CEH,CE=BC,所以△ABE～=△HCE(ASA),所以AE=HE,∠BAE=∠H.因为AE=HE,DE平分∠ADH,所以△ADH是等腰三角形,所以∠DAE=∠H,又因为∠BAE=∠H,所以∠DAE=∠BAE,即AE是∠DAB的平分线.

解法三(利用平行线的性质延长线段)

证明如图4,延长DE及AB,相交于点G.在△GBE和△DCE中,因为∠GBE=∠C,∠BEG=∠DEC,CE=BC,所以△GBE～=△DCE(ASA),所以DE=GE,∠CDE=∠G,又因为DE平分∠ADH,所以∠ADE=∠G,所以△ADG是等腰三角形,又因为DE=GE,所以AE是∠DAB的平分线.

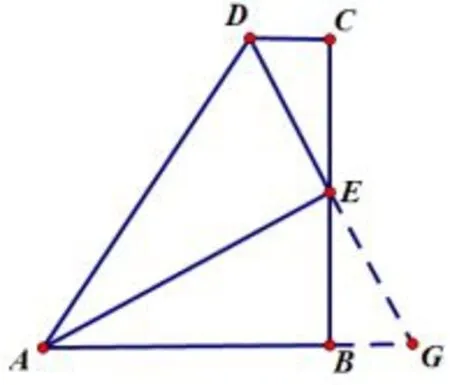
图4

四、问题变式

(一)条件变式

我们把此题的条件∠B=∠C=90°减弱为∠B+∠C=180°,再看看结论是否发生变化?

例2如图5,∠B+∠C=180°,E是BC的中点,DE平分∠ADC.求证：AE是∠DAB的平分线.

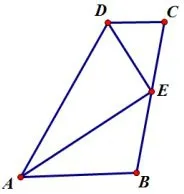
图5

分析例1中的第一种证法是利用角平分线的性质,因为现在不再有∠B=∠C=90°这个条件,以此解法一不再成立,但解法二和解法三因为只涉及到全等,由此变化不大,以下有变动的部分用红色标注.

解法二(利用平行线的性质延长线段)

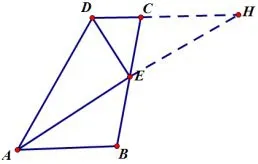
图6

证明如图6,延长AE及DC,相交于点H.因为∠B+∠DCB=180°,又因为∠ECH+∠DCB=180°,所以∠B=∠ECH.在△ABE和△HCE中,因为∠B=∠ECH,∠BEA=∠CEH,CE=BC,所以△ABE～=△HCE(ASA),所以AE=HE,∠BAE=∠H.因为AE=HE,DE平分∠ADH,所以△ADH是等腰三角形,所以∠DAE=∠H,又因为∠BAE=∠H,所以∠DAE=∠BAE,即AE是∠DAB的平分线.

解法三(利用平行线的性质延长线段)

证明如图7,延长DE及AB,相交于点G.因为∠C+∠CBA=180°,又因为∠CBA+∠CBG=180°,所以∠CBG=∠C.在△GBE和△DCE中,因为∠GBE=∠C,∠BEG=∠DEC,CE=BC,所以△GBE～=△DCE(ASA),所以DE=GE,∠CDE=∠G,又因为DE平分∠ADH,所以∠ADE=∠G,所以△ADG是等腰三角形,又因为DE=GE,所以AE是∠DAB的平分线.

反思减弱条件这种变形方式比较常见,教学中教师要引导学生在今后的学习中按照这种方法改编题目,鼓励学生自主探究,对提高学生的几何水平帮助很大.此题变形后的解法二和解法三与原题的解法基本类似,区别主要来自一组角度相等的证明由例1直接告知变为例2的间接证明,难度提升不大,但所蕴含的“类比”思想很重要,应掌握.另外,有学生可能使用截取线段,再证全等的方法用类似解法一来解答例2,大概解法如下：

解法一(利用角平分线的性质截取线段证全等)

证明如图8,在AD上截取DF=DC,在△DEF和△DEC中,因为DF=DC,∠CDE=∠FDE,DE=DE,所以△DEF～=△DEC(SAS),所以CE=EF,又因为E是BC的中点,所以EB=EF.因为△DEF～=△DEC所以∠C=∠DFE,又因为∠DFE+∠AFE=180°且∠C+∠EBA=180°,所以∠EBA=∠EFA.在Rt△AEF和Rt△AEB中,因为AE=AE,EB=EF,∠EBA=∠EFA,所以△AEF～=△AEB(???),所以∠BAE=∠FAE,即AE是∠DAB的平分线.

分析这种截取线段等于已知线段的方法很常见,尤其证明“一条线段的长等于另外两条线段的长”的时候,经常会用截取的办法,这是初中生要掌握的重点方法之一,能想到这种做法的学生是很不错的,应当给予鼓励,但证明过程中的错误也很明显,△AEF与△AEB全等的理由是SSA,不能判定全等.

反思虽然和例1相比,例2解法一证明全等的条件基本相同,但之所以例1可以证明△AEF与△AEB全等,是因为直角三角形HL这个判定,通过这种错误解法的展示,既加深了学生对SSA及HL这两种判定的比较,也加深了SSA这种错误判定的认识.

(二)结论变式

其实在以上证明过程中,细心的读者已经发现例1的三个条件不止能推出AE是∠DAB的平分线这一个结论,所以把原问题的结论加强如下：

例3如图9,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.

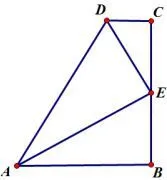
图9

求证：(1)AE是∠DAB的平分线；

(2)AD=AB+CD；

(3)AE⊥DE.

分析此题证明方法与原题类同,也对应了三种做法,此处只说明证法一,其他两种证法略去.

解法一(利用角平分线的性质做垂线)

证明如图10,过点E作EF⊥AD,垂足是F

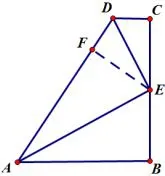
图10

(1)因为DE平分∠ADC,且∠C=∠EFD=90°,所以CE=EF,又因为E是BC的中点,所以EB=EF.在Rt△AEF和Rt△AEB中,因为AE=AE,EB=EF,所以△AEF～=△AEB(HL),所以AF=AB,∠BAE=∠FAE,即AE是∠DAB的平分线.

(2)在 Rt△DEF和 Rt△DEC中,因为DE=DE,CE=EF,所以△DEF～=△DEC(HL),所以DF=DC,又因为AF=AB,所以AD=AB+CD.

(3)因为△AEF～=△AEB,所以∠AEB=∠AEF.因为△DEF～=△EDC,所以∠DEF=∠DEC,又因为∠AEB+∠AEF+∠DEF+∠DEC=180°,所以∠AEF+∠DEF=90°,即AE⊥DE.

反思很多几何题都可以通过增强结论的方法来深入探究,这是我们平时几何教学中的重要补充,应该予以重视.本变形题有例1和例2作铺垫,想必第(2)(3)问的证明并不难,建议在教学中把例3的条件减弱为∠B+∠C=180°再让学生们尝试.

(三)拓广探索

把例2中点条件和结论编号,并罗列如下：

图8

1.∠B+∠C=180°；

2.E是BC的中点；

3.DE平分∠ADC；

4.AE平分∠DAB；

5.AD=AB+CD；

6.AE⊥DE.

思考是不是任意选择三个作为条件,另外三个作为结论,均构成真命题?

分析答案是肯定的.从六个里选择三个共有20种情况,实际教学中可以鼓励学生分组探究,在探究中,鼓励学生参考已取得的证法及证明思路(目前有三类方法：利用角平分线的性质做垂线；利用平行线的性质延长线段；利用角平分线的性质截取线段证全等),尽量自主研究,建议每组研究1-2种情况,最后让学生代表上台展示即可.这里罗列这20种情况,并给予简单证明：(标红的是使用了新的证法)

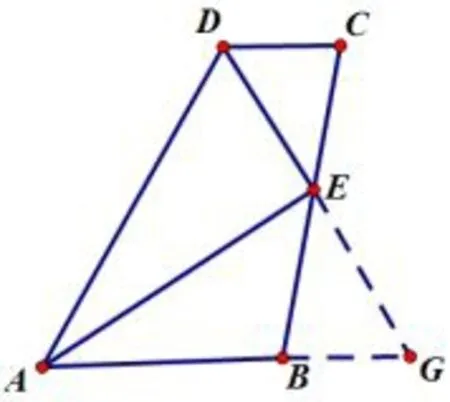
图11

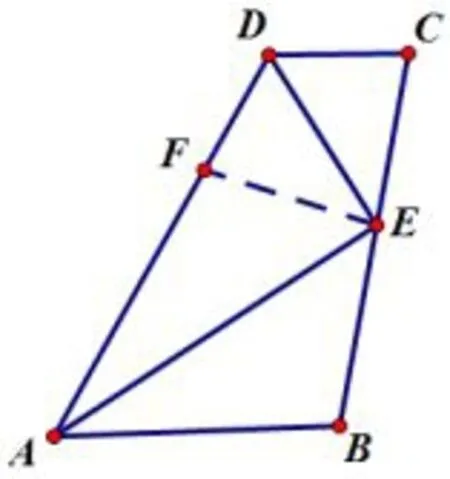
图12

123已证.

124因为3与4有对称性,故证法同123.

125如图11,先证△DCE～=△GBE,再通过等腰△ADG三线合一的性质来证明(利用平行线的性质延长线段).

126如图11,先证△DCE～=△GBE,再用AE是DG垂直平分线的性质来证明(利用平行线的性质延长线段).

134如图11,先说明△ADG是等腰三角形,再利用△ADG三线合一的性质来证明(利用平行线的性质延长线段).

135如图11,先说明△ADG是等腰三角形,再证△DCE～=△GBE(利用平行线的性质延长线段).

136如图11,先说明△ADG是等腰三角形,再利用△ADG三线合一的性质来证明(利用平行线的性质延长线段).

145类似于135(利用平行线的性质延长线段).

146类似于136(利用平行线的性质延长线段).

156如图11,先证△DCE～=△GBE,再用AE是DG垂直平分线的性质来证明(利用平行线的性质延长线段).

234如图11,构造EG=ED,先证△DCE～=△BGE,再证ABG共线(利用中线的性质,延长构造全等,再证共线).

235如图12,截取DF=DC,先证△DCE～=△GFE,再证△ABE～=△AFE(利用角平分线的性质截取线段证全等).

236如图11,构造EG=ED,先证△DCE～=△BGE,再证ABG共线(利用中线的性质,延长构造全等,再证共线).

245类似于235.

256如图11,截取AG=AD,先证△AEG～=△AED,先证△DCE～=△GBE(利用中线的性质,延长构造全等,再证共线).

345如图12,截取DF=DC,先证△DCE～=△GFE,再证△ABE～=△AFE(利用角平分线的性质截取线段证全等).

346如图12,构造∠DEF=∠DEC,先证△DCE～=△DFE,再证△ABE～=△AFE(利用等角的余角相等这个性质,构造全等).

356类似于456.

456如图11,截取AG=AD,先证△AEG～=△AED,先证△DCE～=△GBE.

以上证明中涉及到“构造全等,然后证明共线”这种新的方法,下面以256为例,阐述这种方法.

例4如图13,E是BC的中点,AD=AB+CD,AE⊥DE.

求证：(1)∠B+∠C=180°；

(2)DE平分∠ADC；

(3)AE平分∠DAB.

解法一(利用中线的性质,延长构造全等,再证共线)

证明如图13,延长DE到G,使DE=EG,连BG,AG.

(1)在△DEC和△GEB中,因为DE=EG,CE=BE,∠BEG=∠CED,所以△AEF～=△AEB(SAS),所以DE=EG,又因为AE=AE,∠AEG=∠AED=90°,所以△AEG～=△AED(SAS),所以AG=AD,又因为AD=AB+CD,所以AG=AB+CD,又因为BG=CD,所以AG=AB+BG,即A、B、G共线.

下略.

图13

反思通过对拓广探索部分20个命题的研究,此题已经研究得很透彻了,其中涉及的解法大概有四类：利用角平分线的性质做垂线；利用平行线的性质延长线段；利用角平分线的性质截取线段证全等；中线延长构造全等类.涉及的知识点有：平行线的性质、全等三角形的判定和性质、角平分线的性质和判定、垂直平分线的性质和判定、等腰三角形的性质和判定等,几乎涵盖了七八年级学过的所有几何知识.通过这一道题目及其变式的研究,复习了初中阶段学习的所有几何知识,证明过程中应用了各种常见的证明方法,这说明本次探究及变形是有意义的.

总之,在数学教学中,通过减弱条件、增强结论、条件结论互换等方式改编题目,得到变式,通过充分研究变式,能引导学生进入深层次的思维状态,进而探寻解题策略,培养学生形成解后反思的良好思维习惯,使解题规律化、系统化,以达到触类旁通的效果.